La grande lunette de Meudon, bac Polynésie 2021. Lunette astronomique, lentille convergente, grossissement. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. .. .. . . .. .. ...... ... La grannde lunette est constituée de deux lentilles minces convergentes : L1 de centre optique O1 et de  distance focale f '1 = 16 m. L2 de centre optique O2 et de  distance focale f '2 = 4 cm. 1. Nommer la lentille L1 et L2 en justifiant. 2. Une lunette astronomique est un système afocal. Définir ce terme. Des rayons parallèles entre eux avant le système optique, ressortent parallèles après le système. 3. Indiquer la position des foyers F2 et F '2 sans souci d'échelle de la lentille L2. m : masse du satellite ; M : masse de la lune ; r = R+h ; R rayon de la lune ; h : altitude du satellite. 4. Tracer le trajet du rayon lumineux issu de B pénétrant dans la lunette par le centre optique O1 de la lentille L1 et émergeant de la lentille L2. Noter la position de B1 image intermédiaire de B. B1 est dans le plan focal image de L1. 5. Représenter le faiscerau émergent issu de l'objet B traversant la lunette en poursuivant les trajets des ryons lumineux s'appuyant sur les bords de L1 jusqu'à leur sortie de la lunette par L2. ... .... 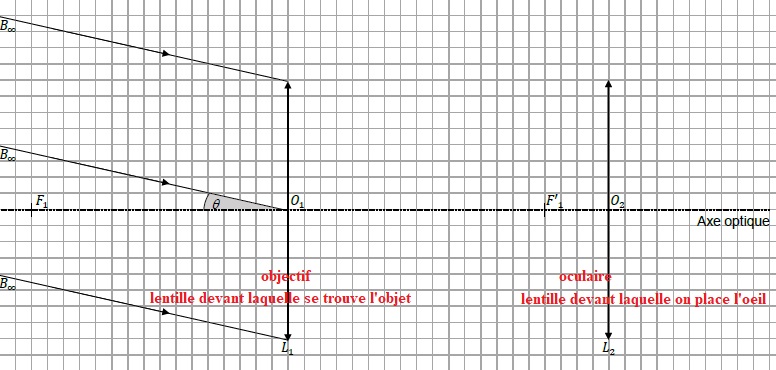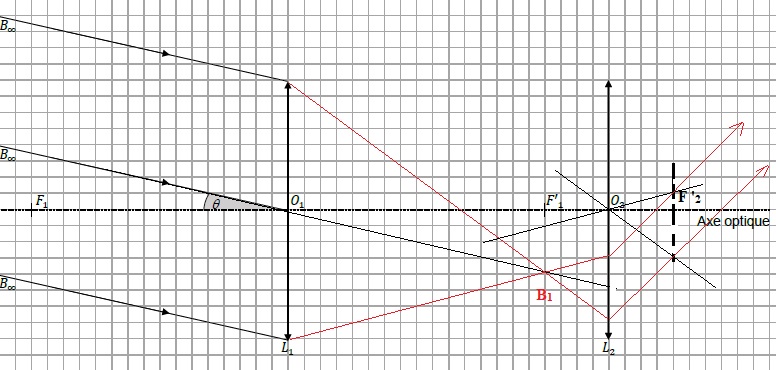6. Le point B est vu à l'oeil nu sous l'angle q appelé diamètre apparent de l'objet. Représenter l'angle q' sous lequel l'image définitive est vue à travers la lunette. 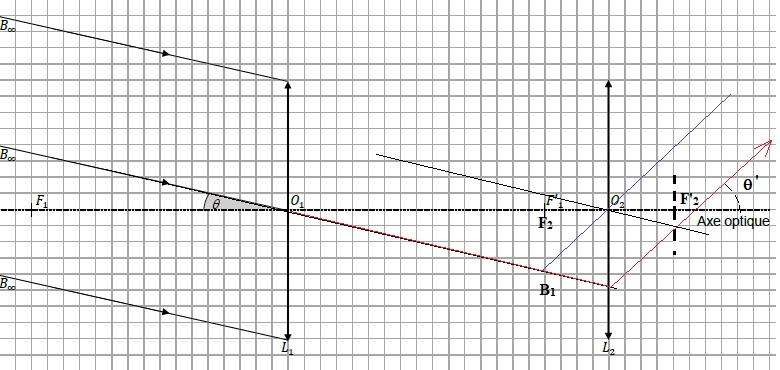7. Le grossissement G de la lunette est donné par G = q' / q. Les angles étant petits tan q ~q radian. Exprimer G en fonction de f '1 et f '2. 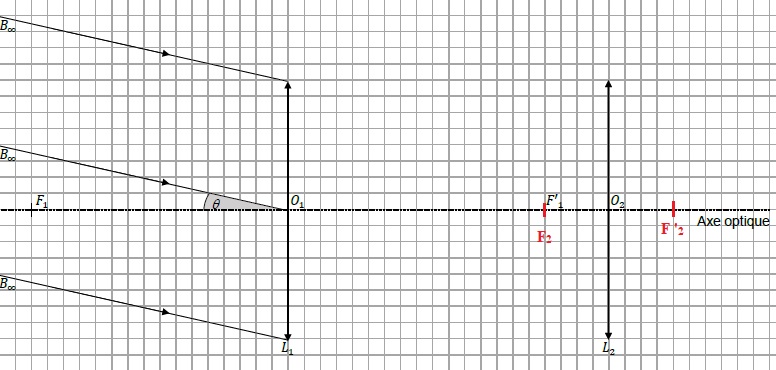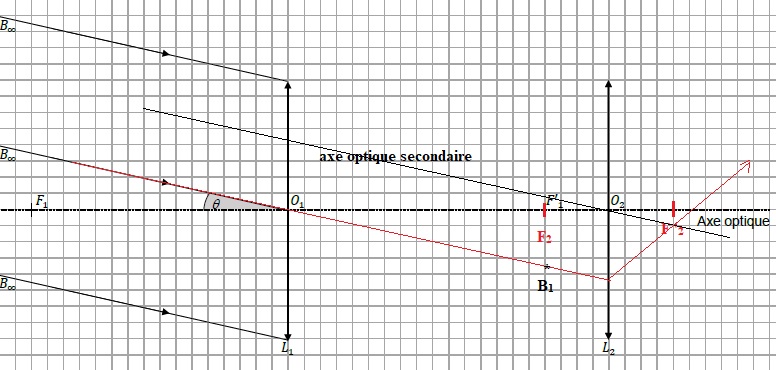Dans le triangle O1B1F '1 : tan q ~q =B1F '1 / O1F '1. Dans le triangle O2B1F2 : tan q' ~q' =B1F '1 / O2F2. |G |= O1F '1 / O2F2 = f '1 / f '2. 8. Calculer G. G = 16 / 0,04 =400. Depuis le sol terrestre, un cratère de la Lune, peut être  aperçu sous un angle q de valeur égale à une minute d'angle. 9. Calculer q' en degré. q ' = 400 q = 400 minutes d'angle soit 400 / 60 ~ 6,7 °.

menu