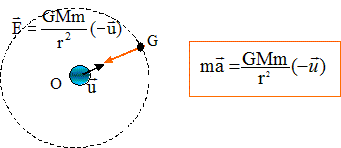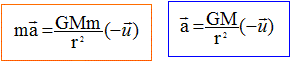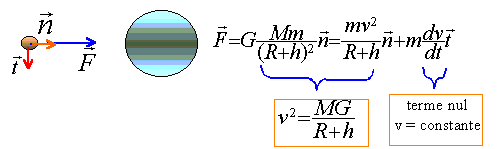L'installation de l'homme sur la lune, bac Polynésie 2021. Satellite, repère de Frenet, chute libre En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. .. .. . . .. .. ...... ... Etude d'un satellite de télécommunication. L'orbite du satellite autour de la lune est circulaire et on néglige l'influence de la terre sur ce  dernier. 1. Proposer une définition d'un satellite lunostationnaire. L'orbite est dans le plan équatorial de la lune. Il tourne à la même vitesse angulaire que la lune. Il est donc fixe pour un observateur situé sur la lune. 2. Représenter la force d'interaction gravitationnelle exercée par la lune sur ce  satellite sanns souci d'échelle. 3. Etablir l'expression de cette force. 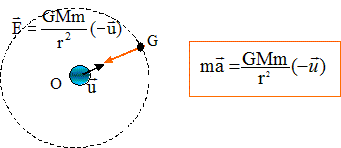m : masse du satellite ; M : masse de la lune ; r = R+h ; R rayon de la lune ; h : altitude du satellite. 4. Etablir l'expression de l'accélération du centre du satellite. 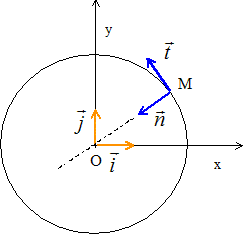La seconde loi de Newton conduit à : 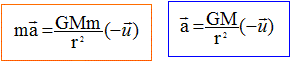5. Représenter les vecteurs unitaires de la base de Frenet. Dans la base de Frenet associée au point M : 6. Citer l'expression des coordonnées du vecteur accélération dans le repère de Frenet dans le cas d'un mouvement circulaire. 7. En déduire l'expression de l'accélération dans ce repère. 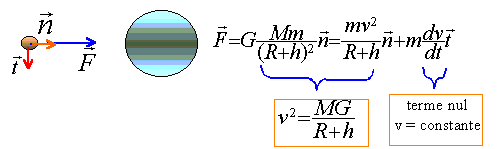L'accélération normale vaut v2 / (R+h) et l'accélération tangentielle est nulle. 8. Justifier que la norme de la vitesse est constante et vaut v = (GM / r)½. L'accélération tangentielle étant nulle : dv / dt = 0 soit v = constante. L'accélération normale vaut : MG / r2 = v2 / r ; v2 = GM / r ; v = (GM / r)½. 9. Démontrer que pour que le satellite soit fixe par rapport à la lune, il doit être à l'altitude h = 8,67 107 m par rapport à la surface de la lune. Période de rotation de la lune sur elle même : T = 27,3 jours soit 2,36 106 s. Masse de la lune  M = 7,34 1022 kg. Rayon de la lune R = 1,74 106 m. G = 6,67 10-11  N m2 kg-2. Le satellite décrit la circonférence 2pr à la vitesse v en T seconde. 2pr = v T. 4p2r2 = v2 T2= GM / rT2  . r3 = GMT2 / (4p2) = 6,67 10-11 x7,34 1022 x(2,36 10,,6)2 / (4x3,142) =6,91 1023. r = 8,84 107 m ; h = r-R = 8,84 107 -1,74 106 =8,67 107 m ... .... 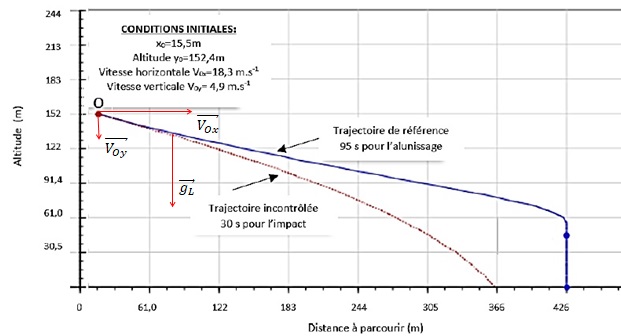Une simulation de l'alunissage a été menée sur un simulateur de mouvement vertical. Elle commence  à 152,4 m d'altitude avec une vitesse horizontale de norme égale à 18,3 m /s et une vitesse verticale  de norme 4,9 m /s. La trajectoire de référennce d'une durée égale à 95 s permet de poser le module lunaire en toute sécurité. La trajectoire incontrolée d'une durée de 30 s conduit à un impact sur le sol lunaire. 10. Représenter au point O les vecteurs vitesses horizontale et verticale sans souci d'échelle. Représenter également le vecteur champ de pesanteur lunaire. 11. Justifier le signe négatif ou positif de chacun des termes de l'équation horaire suivante : y(t) =- 0,5 gL t2 -vOyt +y0. Le premier  terme est négatif car le vecteur champ de pesanteur lunaire est de sens contraire au vecteur unitaire de l'axe vertical. Le second  terme est négatif car le vitesse vertical initiale est de sens contraire au vecteur unitaire de l'axe vertical. Le dernier terme est positif, l'altitude initiale est positive. 12. A l'aide de l'équation horaire suivante, calculer la durée de la descente de l'alunisseur s'il était en chute libre. Indiquer si l'alunisseur dans sa trajectoire incontrôlée est en chute libre. x(t) = vOxt+x0. Lors de la descente en chute libre : x(t) = 426 m. t = (x(t) - x0) / vOx  =(426-15,5) / 18,3 =22,4 s. Dans le cas  d'une trajectoire incontrôlée, la durée de la descente est de 30 s, valeur différente de 22,4 s. La chute n'est pas libre.

menu