Accélérateur linéaire Linac 2, bac général 2021. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. .. .. Cet accélérateur permet de communiquer une vitesse importante aux protons. Les protons initialement au repos atteignent l'énergie de 50 MeV à la sortie de l'accélérateur. les protons passent par une succession de zones modélisables par des condensateurs plans où règne un champ électrique et des zones où ne règne aucun champ électrique. 1. Accélération initiale des protons dans un premier condensateur plan. 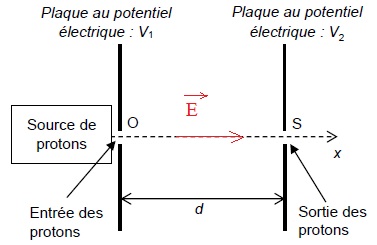Un proton entre dans le condensateur plan avec une vitesse initiale nulle en O. Une tension électrique U = V1-V2 est appliquée entre les plaques du condensateur séparées d'une distance d. Le champ électrique E créé entre les plaques est supposé uniforme, dirigé dans le sens de l'axe Ox et de norme E = U / d. d = 10,0 cm ; U = 2,00 MV. 1.1. Représenter le vecteur champ électrique. 1.2. Comparer la valeur du poids du proton aveccelle de la force électrique à laquelle il est soumis et conclure. Poids = mp g avec mp = 1,67 10-27 kg ; P = 1,67 10-27 x9,81 ~1,6 10-26 N. Force électrique F = e E avec E = U / d = 2,00 106 / 0,10= 2,00 107 V m-1. F = 1,6 10-19 x 2,00 107 ~3,2 10-12 N. Le poids est négligeable devant la force électrique. 1.3 Déterminer l'expression du vecteur accélération du proton et en déduire la nature du mouvement. 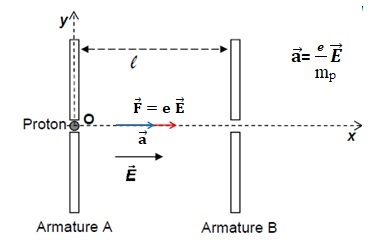Le mouvement du proton est rectiligne uniformément accéléré. 1.5 Montrer que la variation d'énergie cinétique du proton entre O et S est égale à e U. La vitesse initiale étant nulle en O, l'énergie cinétique initiale du proton est nulle. Le proton n'est soumis qu'à la force électrique entre O et S. Le travail de cette force est égal à e U. Variation d'énergie cinétique du proton : Ec finale -0 = eU. 1.6 Donner l'expression de la vityesse vS du proton en S, déterminer sa valeur et commenter. ½mpvs2 = eU ; vs2 = 2eU / mp ; vs =(2eU / mp)½. vs =(2x1,6 10-19 x2,00 106 / (1,67 10-27))½ = 1,96 107 m /s. Cette vitesse n'est pas relativiste. 2. Principe du Linac. Dans une enceinte où règne un vide poussé, on fait passer les protons dans une série de tubes métalliques reliés alternativement à l'une ou à l'autre bornes d'un générateur de tension alternative Ua(t). Cette tension crée, dans les intervalles qui séparent les tubes, un champ électrique dans la direction  Ox. 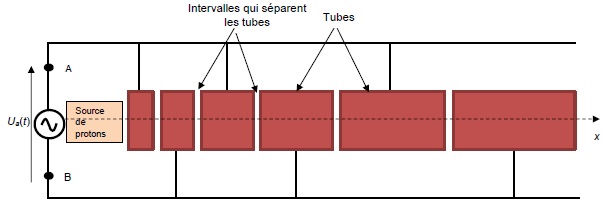Le champ électrique régnant dans les intervalles étant variable au cours du temps, la fréquence de la tension Ua(t) et la longueur des tubes sont choisies très précisément pour que les protons arrivent dans chaque intervalle à l'instant où le sens du champ électrique est tel qu'il permet leur accélération. On considère qu'à l'intérieur des tubes le champ électrique est nul et donc que les particules s'y déplacent à vitesse constante. L'énergie cinétique des protons augmentant au passage de chaque intervalle, l'énergie cinétique atteinte à la sortie de  l'accélérateur dépend, entre autres, du nombre de tubes. L'un des intérês d'un tel dispositif est qu'il suffit d'ajouter des tubes ou d'augmenter la valeur du champ électrique pour augmenter l'énergie cinétique finale des protons. Son principal inconvénient est son encombrement qui est d'une longueur de 34 m. Chaque intervalle se comporte comme un condensateur plan étudié dans la première partie. Le générateur produit une tension sinusoïdale de période T = 40 ns. On donne la variation de la tension Ua en fonction du temps. Si Ua(t) >0, alors VA > VB et si Ua(t) < 0 alors  VA <> VB. 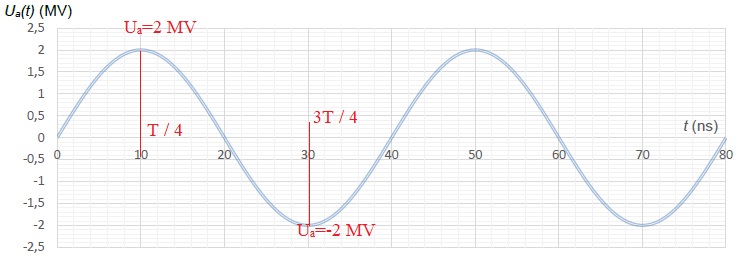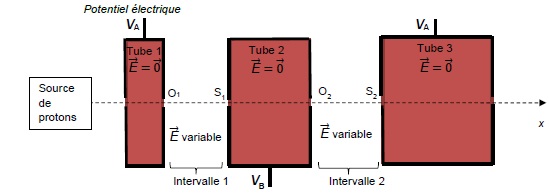2.1. Indiquer le sens du champ électrique qui règne dans l'intervalle 1 et dans l'intervalle 2 entre les tubes à l'instant T /4. Représenter ces champs électriques.   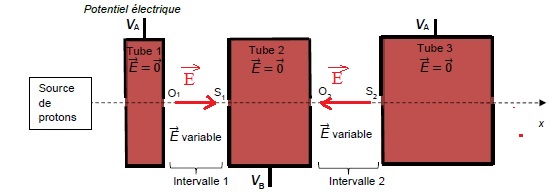A t = T /4, Ua(t) >0, alors VA > VB et le champ électrique pointe vers le plus petit potentiel, S1 dans l'intervalle 1 et vers O2 dans l'intervalle 2. 2.3. Même question à t = 3T /4. 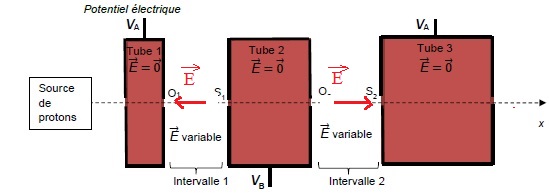A t = 3T /4, Ua(t) < 0, alors VA < VB et le champ électrique pointe vers le plus petit potentiel, O1 dans l'intervalle 1 et vers S2 dans l'intervalle 2. 2.3. Pour être accélérés de manière optimale dans chaque intervalle, les protons doivent mettre une durée Dt = T /2 pour traverser chaque tube. Justifier. A t = T /4, Ua(t) est positive et maximale alors, VA > VB et le champ électrique pointe vers le plus petit potentiel, S1 dans l'intervalle 1 et vers O2 dans l'intervalle 2. A t = 3 T / 4, pour être accéléré de manière optimale, |Ua(t) |doit être maximale. La durée du passage entre les tubes doit être égale à ½T. 2.4. Expliquer qualittivement pourquoi les tubes doivent être de plus en plus longs. La vitesse des protons augmente et la durée du passage entre les tubes est constante, égale à ½T.. Un vitesse est une longueur divisée par une durée. La longueur des tubes doit donc croître.

menu