Un vol inaugural un peu particulier, mouvement de la planète Mars, échange thermique. E3C terminale. 

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

.. ..

Retour des propulseurs latéraux sur terre.
Après séparation du propulseur principal, les propulseurs latéraux effectuent une manoeuvre de retournement. La descente alterne des phases où les réacteurs sont allumés et des phases où ils sont tous éteints. On s'intéresse à la phase finale de descente verticale. L'origine des temps est prise au moment du décollage. L'axe vertical Oz est orienté vers le haut, son origine est au sol.
On donne l'évolution de la vitesse et de l'altitude d'un propulseur pendant les 80 s précédant l'atterrissage.

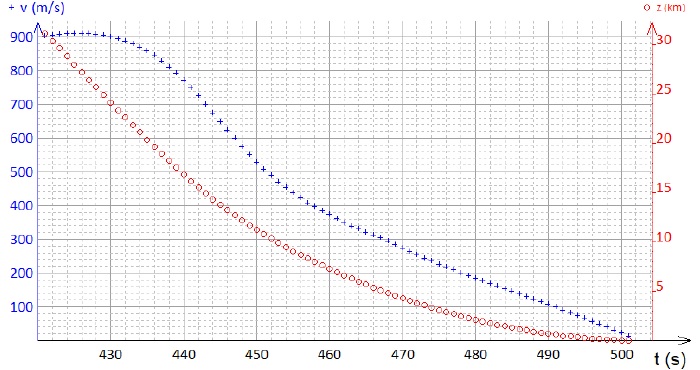1. Interpréter le fait que la vitesse est pratiquement constante entre 420 et 430 s alors que le moteurs sont éteints.
La chute est verticale et à vitesse constante entre t = 420 et 430 s ( mouvement vertical uniforme ). D'après le principe d'inertie, le poids et les frottements sur les couches d'air raréfié se compensent.
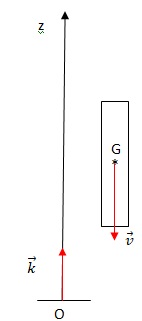
2.1. Faire un schéma de la situation lors de la descente sur lequel figurent l'axe Oz, son vecteur unitaire, le point G et le vecteur vitesse du centre de masse.

2.2. Rappeler la définition du vecteur vitesse du centre de masse G.
Le vecteur vitesse est la dérivée du vecteur position par rapport au temps.
2.3. Etablir la relation entre la norme de la vitesse v et la dérivée de l'altitude z par rapport au temps.
L'altitude diminue  dz < 0 , la norme de la vitesse est positive : v = -dz / dt.
Entre 420 et 430 s, la diminution de l'altitude est à peu près linéaire et en conséquence la vitesse est pratiquement constante.
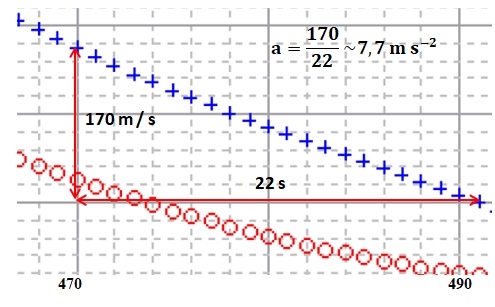
3. Déterminer graphiquement la valeur de la norme du vecteur accélération de G à t > 467 s.

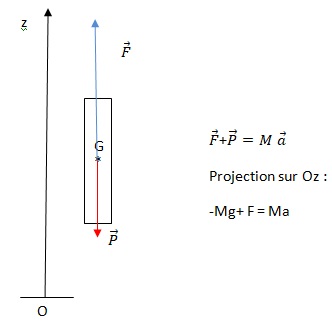
4.1. Dans les 4 dernières secondes, la résistance de l'air est négligeable ; la masse M du propulseur est constante. On note F la force dite de poussée exercée par un unique moteur Merlin en marche. Représenter sur un schéma les forces exercées sur le propulseur.
Le propulseur est soumis à
- son poids, verticale vers le bas, valeur Mg = 25,3 103 *9,81 ~2,48 105 N : 245 kN
-  à la poussée du moteur, verticale vers le haut.
 et à la poussée d'Archimède, verticale vers le haut :
Volume du propulseur cylindrique de hauteur 44,6 m et de diamètre 3,66 m : V = 470 m3.
rair V g = 1,3 x470 x9,81 ~6 kN, négligeable.

 Valeur de la poussée du moteur : M(a+g) =25,3 103( 9,81 +7,7) ~443 kN.

.
.

Mouvement de la planète Mars autour du soleil.
On considère que la planète Mars effectue un mouvement circulaire autour du Soleil. L'étude est conduite dans le référentiel héliocentrique.
Représenter la force exercée par le Soleil sur Mars. Etablir l'expression du vecteur accélération du centre de Mars.

Mars n'est soumis qu'à la force de gravitation, centripète, exercée par le soleil. Le mouvement de Mars est uniforme dans le référentiel héliocentrique.
En déduire l'expression puis la valeur de la vitesse de Mars dans ce référentiel.
v2 = GMS / MS.
v = (GMS / MS)½ = (1,99 1030 x 6,67 10-11 / (2,28 1011))½ ~2,4 104 m /s.
Exprimer la période T de révolution de Mars autour du Soleil. Vérifier par calcul qu'elle est voisine de 690 jours.
Mars décrit la circonférence 2p MS à la vitesse v en T seconde.
T = 2p MS / v = 2 x3,14 x2,28 1011 / ( 2,4 104) ~5,9 107 s ( ~690 jours).

Davantage de carburant dans un même volume.
Les moteurs brûlent un mélange de dioxygène liquide ( LOX) et de kérosène. Le carburant et le combustible circulent dans un bain d'azote liquide afin d'en stocker un maximum dans un même volume, sous une pression de 5 bars. Le LOX est refroidit à -207 °C ( 66 K). Le réservoir de dioxygène a été ainsi racourci et celui de kérosène allongé.
1. Indiquer le sens du transfert d'énergie qui s'effectue entre le LOX et le diazote liquide.
Le transfert d'énergie s'effectue du corps chaud ( le LOX) vers le corps froid ( le diazote liquide). Un partie de ce dernier peut passer sous forme gazeuse.
 Exprimer puis calculer, l'énergie échangée entre le LOX et le diazote lors du refroidissement de 10 ° C du LOX.
Masse de LOX stockée dans le réservoir d'un propulseur latéral : M = 287,4 t.
Capacité thermique massique du LOX à 66 K : c = 1659 J kg-1 K-1.
M c Dq =287,4 103 x 1659 x10 =4,77 109 J.

Lorsque le réservoir du LOX est rempli, il est au contact de la paroi du réservoir elle-même en contact avec l''air ambiant. Ce réservoir est monocoque et constitué d'un alliage d'aluminium et de lithium. On s'intéresse à la durée approximative à l'issue de laquelle la température du LOX risque de réaugmenter de 10 °C, ce qui ferait perdre le bénéfice du refroidissement.
L'air extérieur est considéré comme un système à température constante Tair.
Le flux thermique de l'air vers le LOX à température T s'exprime par : P = h S (Tair-T) où S est la surface de contact et h une constante caractéristique de l'échange thermique.
2. A l'aide d'un bilan énergétique, établir que l'équation différentielle vérifiée par la température  du LOX s'écrit :  McdT /dt = h S (Tair- T).
Pendant la durée dt la température du LOX varie de dT :
énergie échangée entre le diazote et le LOX : M c dT.
énergie échangée entre l'air et le LOX : Pdt = h S (Tair-T)dt.
En régime permanent, bilan énergétique : M c dT =h S (Tair-T)dt.
McdT /dt = h S (Tair- T).
3. En déduire que l'expression de la température du LOX au cours du temps s'écrit T(t) = Tair + A exp(-t / t).
dT / dt +hS / (Mc) T =h S / (Mc) Tair (1)
On pose t =Mc / (hS), constante de temps, caractéristique de l'évolution de la température au cours du temps. Cette valeur sera atteinte au bout d'un temps infini.
Solution générale de dT / dt + T / t =0 : T= A exp(-t / t).
Solution particulière de (1) : T = Tair.
Solution générale de (1) : T(t) = Tair + A exp(-t / t).
A l'instant initial T(t=0) = 66 K ; 66 = Tair +A ; A = 66-Tair.
T(t) = Tair + (66-Tair) exp(-t / t).
T(t) =66 exp(-t / t) +Tair (1-exp(-t / t)).
4. Les courbes suivantes sont obtenues par simulation pour deux valeurs de h : h1 = 1,0 W K-1 m2 et h2 = 60 W K-1 m2.
t et h varient en sens contraire. Si h est plus élevé, la constante de temps est la plus faible ( courbe A).

 La courbe B correspond le mieux à la situation réelle étudiée. La température du LOX augmente de 10 °C au bout d'environ 25 heures ( 1 jour).
Le remplissage du LOX se fait 45 minutes avant le décollage : le bénéfice du refroidissement. n'et pas perdu.
5. Justifier que quelle que soit la valeur de h, la dérivée de la température par rapport au temps dT /dt peut être considérée comme constante au début du réchauffement ( par exemple pour les 10 premiers degrés).
 Equation différentielle : dT / dt =h S / (Mc)( Tair -T).

.


  

menu