Puissance rayonnée par la lune, bac septembre 2021.

En 1939, les physiciens Pettit et Nicholson ont étudié la température de surface de la Lune à partir de la mesure de la puissance émise par la Lune lors de l’éclipse lunaire du 28 octobre 1939.
Cet exercice décrit une expérience menée au laboratoire pour déterminer la puissance lumineuse surfacique au niveau de la surface de la Terre lors d’une pleine Lune.
On s’intéresse d’abord à un dispositif de détection qui permet de capter la lumière issue de la Lune, puis on étudie un capteur thermique afin de déterminer la puissance lumineuse surfacique rayonnée lors d’une pleine Lune sur le sol terrestre.
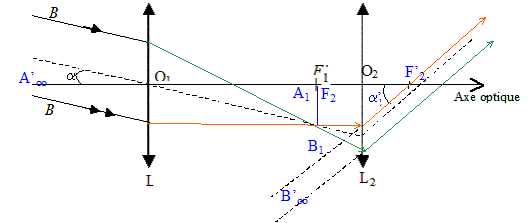
1. Dispositif optique de détection.
Pour déterminer la puissance émise par la Lune, Edison Pettit a placé un capteur de température au foyer du télescope du Mont Wilson.
On reproduit l’expérience de Pettit au laboratoire en utilisant une lunette afocale. La lumière diffusée par la Lune est ainsi concentrée sur un capteur de température fixé au foyer image de l’objectif de la lunette.
L’objectif de la lunette est modélisé par une lentille convergente de distance focale f₁’ = 101 cm, l’oculaire est modélisé par une lentille convergente de distance focale f₂’.
Le capteur de température se présente sous la forme d’un petit carré noir de 0,8 mm de côté.
1.1 Énoncer la condition sur les positions du foyer image de l’objectif et du foyer objet de l’oculaire pour que la lunette soit afocale.
Le foyer image de l’objectif et le foyer objet de l’oculaire sont confondus.
1.2 Préciser sur le schéma de la lunette afocale, la position du capteur de température.
Le capteur de température fixé au foyer image de l’objectif de la lunette.
1.3 Représenter sur ce même schéma, le faisceau émergent issu d’une région d’un astre lointain incliné d’un angle α par rapport à l'axe optique et traversant la lunette afocale.

1.4 La « Mer » de la Tranquillité est une vaste plaine circulaire facilement repérable sur la Lune. L’axe de la lunette est pointé sur le centre de la « Mer » de la Tranquillité. L’angle sous lequel on voit cette région à l’oeil nu depuis la Terre est 2α = 2,3·10^-3 rad.
Pour optimiser la mesure, le capteur de température doit être au moins éclairé par l’image de la zone étudiée.
Déterminer si la taille de l’image intermédiaire permet une mesure optimale.
tan a ~ a =A₁B₁ / O₁F _'1.

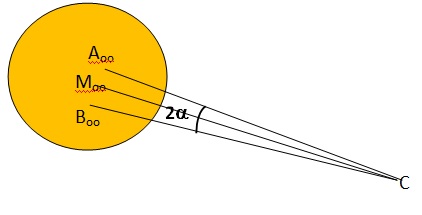
Image de A_oo : A₁M ~ f '₁ a ; Image de B_oo : B₁M ~ f '₁ a ;
Image de A_ooB_oo : A₁M +B₁M ~2 f '₁ a ;
1,15 10^-3 x2 x1,01 ~2,3 10^-3m ~ 2,3 mm, valeur inférieure à la taille du capteur.
La taille de l’image intermédiaire permet une mesure optimale.

2. Étude du capteur de température exposé au rayonnement du Soleil
On étudie maintenant un capteur de température de type « thermocouple » de capacité thermique C. La température indiquée par ce capteur peut être reliée à la puissance rayonnée qu’il reçoit.
Pour déterminer la résistance thermique R_th liée au transfert thermique entre le milieu extérieur et le capteur, on étudie le comportement au cours du temps du capteur exposé directement au rayonnement solaire (sans utiliser la lunette étudiée précédemment).
La température du milieu extérieur dans lequel se trouve le capteur est supposée constante et notée T₀pendant toute la durée de l’expérience.
 L’étude est conduite entre t et t + Δt, Δt est supposé petit devant la durée typique de l’évolution de la température du thermocouple.
 À l’état initial t = 0 s, le capteur est dans l’obscurité et à l’équilibre thermique : sa température est égale à T₀.
 À t > 0 s, on expose le capteur à la lumière du Soleil ce qui fait augmenter sa température T. On note P_lumla puissance lumineuse reçue par le capteur, elle est supposée constante.
Il se produit alors un transfert thermique du capteur de température T vers le milieu extérieur de température T₀. Dans la suite de l’exercice, le capteur est choisi comme système.
2.1. La puissance thermique échangée avec le milieu extérieur par le système a pour expression :
P_th =(T₀-T) / R_th.
2.2. Commenter le signe de cette puissance.
Il se produit alors un transfert thermique du capteur de température T vers le milieu extérieur de température T₀. Le système cède de la puissance dans le milieu extérieur. P_th est négative.
2.3. Exprimer la variation d’énergie interne du capteur DU en fonction de sa capacité thermique et de la variation DT de sa température au cours du temps Dt.
DU = C DT= C(T(t) -T₀).
2.4. Relier la variation d’énergie interne DU du capteur à la puissance thermique P_th et à la puissance lumineuse reçue P_lum pendant une durée DT.
DU / Dt = P_lum +P_th .
2.5. En déduire pour des durées Dt tendant vers 0 que la température T(t) du capteur de température vérifie
l’équation différentielle suivante :
dT / dt + T(t) /(R_th × C)=T₀ /(R_th × C) +P_lum / C.

C(T(t) -T₀) / dt =P_lum +P_th .
C(T(t) -T₀) / dt =P_lum +(T₀-T) / R_th.
(T(t) -T₀) / dt =P_lum / C +T₀ / (R_th C)-T(t) / (R_th C).
dT / dt + T(t) /(R_th × C)=T₀ /(R_th × C) +P_lum / C.

2.6. Lorsque la température finale est atteinte par le capteur au bout d’une durée suffisamment longue, l’expression de la puissance lumineuse est P_lum= (T∞-T₀) / R_thavec T∞ la température finale atteinte par le capteur.
Retrouver cette expression à partir de l’équation différentielle de la question 2.5.
Au bout d'une durée suffisamment longue : dT / dt =0.
T∞ /(R_th × C)=T₀ /(R_th × C) +P_lum / C.
T∞ / R_th =T₀ /R_th +P_lum .
T∞ / R_th -T₀ /R_th =P_lum.
P_lum= (T∞-T₀) / R_th.

On admet que l’étude expérimentale permet de déterminer la valeur de la résistance thermique : R_th = 3x10⁴ K.W^–1.