Mathématiques,
fonction, suite récurrente, probabilités, bac septembre 2021.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
..
..
|
.
.
|
..
..
......
...
|
QCM. 4 points.
Une seule réponse exacte.
Aucune justification
n'est demandée.
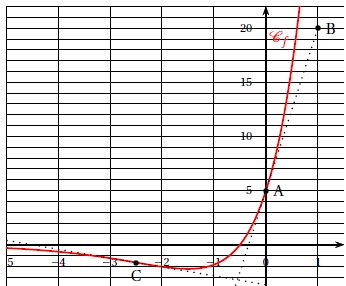
Le graphique ci-dessous donne la représentation graphique Cf
dans un repère orthogonal d’une fonction f définie et dérivable sur R.
On notera f ′ la fonction dérivée de f .
On donne les points A de coordonnées (0; 5) et B de coordonnées (1;
20). Le point C est le point de la courbe Cf ayant
pour abscisse −2,5 . La droite (AB) est la tangente à la courbe Cf
au point A.
Les questions 1 à 3 se rapportent à cette même fonction f .
1. On peut affirmer que :
a. f ′(−0,5) = 0.
b. si x ∈]−∞;
−0,5[, alors f ′(x) < 0
c. f ′(0) = 15. Vrai.
Le coefficient directeur
de la tangente à la courbe au point A vaut 15.
d. la fonction
dérivée f ′ ne change pas de signe sur R.
2. On admet que la
fonction f représentée ci-dessus est définie sur R par f (x) = (ax +b)ex
, où a et b sont deux nombres réels et que sa courbe coupe l’axe des
abscisses en son point de coordonnées (−0,5 ; 0).
On peut affirmer que :
a. a = 10 et b =5. Vrai.
b. a = 2,5 et b =
−0,5
c. a = −1,5 et b =
5.
d. a = 0 et b = 5.
f(-0,5) =(-0,5 a+b)e-0,5
= 0 soit -0,5 a+b = 0 : b = 0,5 a.
3. On admet que la
dérivée seconde de la fonction f est définie sur par :
f ′′(x) = (10x +25)ex .
On peut affirmer que :
a. La fonction f
est convexe sur R
b. La fonction f
est concave sur R
c. Le point C est
l’unique point d’inflexion de Cf. Vrai.
d. Cf
n’admet pas de point d’inflexion.
ex
< 0 ; 10 x +25 >0 si x > -2,5 et f est convexe sur ]
-2,5 ; + oo[.
10 x +25 <0 si x < -2,5 et f
est concave sur ] -oo ; -2,5[.
f "=0 si x = -2,5, la
dérivée seconde s'annule et change de signe.
4. On considère deux suites (Un)
et (Vn) définies sur N telles que :
• pour tout entier naturel n, Un < Vn ;
La limite de (Vn) est égale à 2 en plus l'infini.
On peut affirmer que :
a. la suite (Un)
converge
b. pour tout entier
naturel n, Vn <
2
c. la suite (Un)
diverge
d. la suite (Un)
est majorée.
Un < Vn et Vn
< 2 :
donc la suite (Un)
est majorée.
Suite récurrente. 5 points.
Soit f la fonction définie sur l’intervalle ¸] -1 /3 ; +oo[· par :
f (x) =4x / (1+3x)
On considère la suite (un) définie par : u0 =0,5
et, pour tout entier naturel n, un+1 = f (un).
1. Calculer u1
.
u1
= f (u0)=2 / (1+1,5) = 2 / 2,5 = 0,8.
2. On admet
que la fonction f est croissante sur l’intervalle ¸] -1 /3 ; +oo[
a. Montrer par
récurrence que, pour tout entier naturel n, on a : 0,5 < un < un+1
< 2.
Initialisation
: u0
=0,5 ; u1 = 0,8, donc 0,5 < u0 < u1
< 2. La
propriété est vraie au rang zéro.
Hérédité :
on suppose la propriété vraie au rang n soit : 0,5 < un < un+1
< 2.
La fonction f est croissante sur l’intervalle ¸] -1 /3 ; +oo[, donc f(0,5)
< f(un)
< f(un+1) <
f(2).
0,8 < un+1
< un+2 < f(2) =8 /7.
La propriété est donc vraie au rang n+1.
Conclusion
: la propriété est vraie au rang zéro et héréditaire, elle est
vraie pour tout entier n.
b. En déduire
que la suite (un) est convergente.
La suite (un) est croissante et majorée, donc elle converge.
c. On appelle ℓ la
limite de la suite (un). Déterminer la valeur de ℓ.
un+1
= f (un) .l
= f(l) ; l =4l / (1+3l)
l+3l2 =4l ; 3l2 =3l ; l =1.
3. a. Recopier et compléter la
fonction Python ci-dessous qui, pour tout réel positif E,
détermine la plus petite valeur P tel que : 1−uP < E.
def seuil(E) :
u = 0,5
n = 0
while 1-u < E
u = 4*u / (1+3*u)
n=n+1
return n
b. Donner la valeur
renvoyée par ce programme dans le cas où E = 10−4.
1-4x /
(1+3x) < 10-4.
1+3x-4x < 10-4(1+3x).
1-x < 10-4 +3 10-4 x.
1-10-4 < (1+3 10-4) x.
x >(1-10-4) / (1+3 10-4).
x
~0,99990.
n
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
u
|
0,5
|
0,8
|
0,94117
|
0,9846
|
0,9961
|
0,9990
|
0,99975
|
0,99994
|
Le programme renvoie 7.
4.
On considère la suite (vn) définie, pour tout entier naturel
n, par :
vn =un / (1−un)
a. Montrer que la
suite (vn) est géométrique de raison 4 .
En
déduire, pour tout entier naturel n, l’expression de vn en
fonction de n.
vn+1 =un+1 / (1−un+1).
un+1 =4un / (1+3un)
; 1−un+1=(1+3un-4un)
/ (1+3un) =(1-un)
/ (1+3un).
vn+1 =4un /(1-un)= 4 vn.
La suite (vn) est géométrique de raison 4.
vn = v0 4n
; v0
=u0 / (1−u0)= 0,5 / (1-0,5) = 1.
b. Démontrer
que, pour tout entier naturel n, on a : un = vn /
(vn +1).
vn
=un / (1−un) ; (1−un)vn
=un ; vn -un vn = un
; un(1+vn) = vn ; un = vn
/ (vn +1).
c. Montrer alors
que, pour tout entier naturel n , on a :
un =1/(1+0,25n).
Retrouver par le calcul la limite de la suite (un).
un = vn / (vn
+1)=4n /(4n+1)= 1 / (1+0,25n).
-1 < 0,25 < 1,alors 0,25n tend vers zéro si n tend vers
plus l'infini et un tend vers 1.
|
...
|
....
|
Probabilités (5 points).
Partie I.
Dans le parc national des Pyrénées, un chercheur travaille sur le
déclin d’une espèce protégée dans les lacs de haute-montagne : le «
crapaud accoucheur ».
Les parties I et II peuvent être abordées de façon indépendante.
Partie I : Effet
de l’introduction d’une nouvelle espèce.
Dans certains lacs des Pyrénées, des truites ont été introduites par
l’homme afin de permettre des activités de pêche en montagne. Le chercheur a étudié l’impact de
cette introduction sur la population de crapauds accoucheurs d’un lac.
Ses études précédentes l’amènent à modéliser l’évolution de cette
population en fonction du temps par la fonction f suivante :
f (t )= (0,04t 2 −8t +400)et/50 +40 pour t ∈ [0 ; 120]
La variable t représente le temps écoulé, en jour, à partir de
l’introduction à l’instant t = 0 des truites dans le lac, et f (t )modélise le nombre de crapauds à
l’instant t .
1. Déterminer le nombre de crapauds présents dans le lac lors de
l’introduction des truites.
f(0) =400 +40 = 440.
2. On admet que la fonction f est dérivable sur l’intervalle [0; 120]
et on note f ′ sa fonction dérivée.
Montrer, en faisant apparaitre les étapes du calcul, que pour tout
nombre réel t appartenant à l’intervalle [0; 120] on a :
f ′(t )= t (t −100)et/50 ×8×10−4.
3. Étudier les variations de la fonction f sur l’intervalle [0; 120],
puis dresser le tableau de variations de f sur cet intervalle (on donnera des valeurs
approchées au centième).
On pose u =0,04t 2 −8t +400 et v =et/50 .
u' = 0,08 t-8 ; v' = 0,02 et/50 .
u'v + v'u = 0,08(t-100)et/50 + 0,02(0,04t 2 −8t +400 )et/50.
f '(t) = 0,08et/50(t-100+0,01 t2-2t+100) =0,08et/50(0,01 t2-t)=0,08et/50(0,01 t- 1)t.
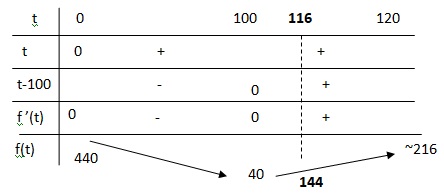
4. Selon cette modélisation :
a. Déterminer le nombre de jours J nécessaires afin que le nombre de
crapauds atteigne son minimum. Quel est ce nombre minimum ?
Au bout de 100 jours il y a 40 crapauds.
b. Justifier que, après avoir atteint son minimum, le nombre de crapauds
dépassera un jour 140 individus.
c. À l’aide de la calculatrice, déterminer la durée en jour à partir de
laquelle le nombre de crapauds dépassera 140 individus ?
Partie II : Effet de la Chytridiomycose sur une population de têtards.
Une des principales causes du déclin de cette espèce de crapaud en
haute montagne est une maladie, la « Chytridiomycose », provoquée par un champignon.
Le chercheur considère que :
• Les trois quarts des lacs de montagne des Pyrénées ne sont pas
infectés par le champignon, c’est-à- dire qu’ils ne contiennent aucun têtard (larve du crapaud)
contaminé.
• Dans les lacs restants, la probabilité qu’un têtard soit contaminé
est de 0,74.
Le chercheur choisit au hasard un lac des Pyrénées, et y procède à des
prélèvements.
Pour la suite de l’exercice, les résultats seront arrondis au millième
lorsque cela est nécessaire.
Le chercheur prélève au hasard un têtard du lac choisi afin d’effectuer
un test avant de le relâcher.
On notera T l’évènement « Le têtard est contaminé par la maladie » et L
l’évènement « Le lac est infecté par le champignon ».
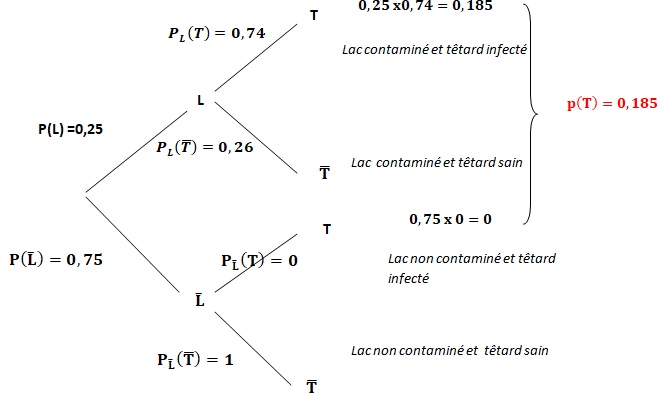
1. Recopier et compléter l’arbre de probabilité suivant en utilisant
les données de l’énoncé :
2. Montrer que la probabilité P(T ) que le têtard prélevé soit
contaminé est de 0,185.
3. Le têtard n’est pas contaminé. Quelle est la probabilité que le lac
soit infecté ?
Pnon T (L) =P(non T n L) / P(non T) =0,25 x 0,26 / (1-0,185)=0,0798.
|
|


