Mathématiques, suites récurrentes, logarithme, bac septembre 2021. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. .. .. . . .. .. ...... ... Suites récurrentes. 5 points On considère les suites (un) et (vn) définies par : u0 = 16 ; v0 =5 ; et pour tout entier naturel n : un+1=(3un +2vn) / 5. vn+1 =(un +vn) / 2. 1. Calculer u1 et v1. u1=(3u0 +2v0) / 5 =(48+10) / 5 =11,6. v1 =(u0 +v0) / 2 =21 / 2 = 10,5. 2. On considère la suite (wn) définie pour tout entier naturel n par : wn = un −vn. a. Démontrer que la suite (wn) est géométrique de raison 0,1. En déduire, pour tout entier naturel n, l’expression de wn en fonction de n. wn+1 = un+1 −vn+1. wn+1 =(3un +2vn) / 5 - (un +vn) / 2. wn+1 =(6un +4vn-5un -5vn) / 10 = (un −vn) / 10 = wn /10. wn =w0 0,1n=16 x0,1n. b. Préciser le signe de la suite (wn) et la limite de cette suite. wn >0 . -1 < 0,1 < 1, alors 0,1n tend vers zéro si n tend vers plus l'infini. La limite de la suite (wn) est égale à zéro. 3. a. Démontrer que, pour tout entier naturel n, on a : un+1 −un = −0,4wn. un+1-un=(3un +2vn) / 5 -5 un / 5 =(-2un +2vn) / 5 = -0,4 wn b. En déduire que la suite (un) est décroissante. wn > 0  ; −0,4wn.< 0 ; un+1-un< 0 ; un+1< un. La suite (un) est donc décroissante.  On peut démontrer de la même manière que la suite (vn) est croissante. On admet ce résultat, et on remarque qu’on a alors : pour tout entier naturel n, vn >v0 =5. c. Démontrer par récurrence que, pour tout entier naturel n, on a : un >5. En déduire que la suite (un) est convergente. On appelle ℓ la limite de (un). Initialisation : u0 = 16, la propriété est vraie au rang zéro. Hérédité : la propriété est supposée vraie au rang n soit un > 5. un+1=(3un +2vn) / 5 et un > 5. et vn > 5, alors : (3un +2vn )/ 5 >25 / 5 =5. Donc  un+1 > 5. Conclusion : la propriété est vraie au rang zéro et héréditaire, elle est vraie pour tout entier n. La suite (un ) est décroissante et bornée, elle est donc convergente. On peut démontrer de la même manière que la suite (vn) est convergente. On admet ce résultat, et on appelle ℓ′ la limite de (vn). 4. a. Démontrer que ℓ = ℓ′. wn = un −vn. La limite de la suite (wn) est égale à zéro. ℓ - ℓ′=0. b. On considère la suite (cn) définie pour tout entier naturel n par : cn = 5un +4vn. Démontrer que la suite (cn) est constante, c’est-à-dire que pour tout entier naturel n, on a : cn+1 = cn. En déduire que, pour tout entier naturel n , cn = 100. cn+1 = 5un+1 +4vn+1 = 3un +2vn+2un +2vn=5un +4vn = Cn. cn =c0 = 5u0 +4v0 =5 x16 + 4 x5 = 100. c. Déterminer la valeur commune des limites ℓ et ℓ′. 100 = 5un +4vn. wn = un −vn. wn tend vers zéro si n devient grand, donc ℓ = ℓ′. 100 = 5 ℓ +4ℓ′ = 9 ℓ  = 9ℓ′ . ℓ′ = ℓ = 100 / 9. ... .... Logarithme (5 points). Partie 1. 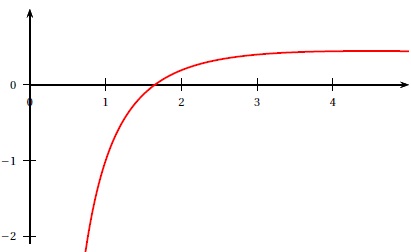Le graphique ci-dessous donne la représentation graphique dans un repère orthonormé de la fonction f définie sur l’intervalle ]0 ; +∞[ par : f (x) =(2ln(x)−1) / x. 1. Déterminer par le calcul l’unique solution α de l’équation f (x) =0. 2ln(a)−1 = 0 ; ln(a) = 0,5 ; a = e0,5~1,65. On donnera la valeur exacte de α ainsi que la valeur arrondie au centième. 2. Préciser, par lecture graphique, le signe de f (x) lorsque x varie dans l’intervalle ]0 ; +∞[. f(x) < 0 sur ] -oo ; a [. f(x) > 0 sur ]  a ; +oo [. Partie II. On considère la fonction g définie sur l’intervalle ]0 ; +∞[ par : g(x) = [ln(x)]2−ln(x). 1. a. Déterminer la limite de la fonction g en 0. g(x) = ln(x) ( ln(x)-1). ln(x) et ln(x)-1 tendent vers moins l'infini quand x tend vers zéro. g(x) tend vers plus l'infini si x tend vers zéro. b. Déterminer la limite de la fonction g en +∞. ln(x) et ln(x)-1 tendent vers plus l'infini quand x tend vers plus l'infini. g(x) tend vers plus l'infini si x tend vers plus l'infini. 2. On note g′ la fonction dérivée de la fonction g sur l’intervalle ]0 ; +∞[. Démontrer que, pour tout nombre réel x de ]0 ; +∞[, on a : g′(x) = f (x), où f désigne la fonction définie dans la partie I. g'(x) = 2 ln(x) / x -1 /x = (2ln(x) -1) / x = f(x). 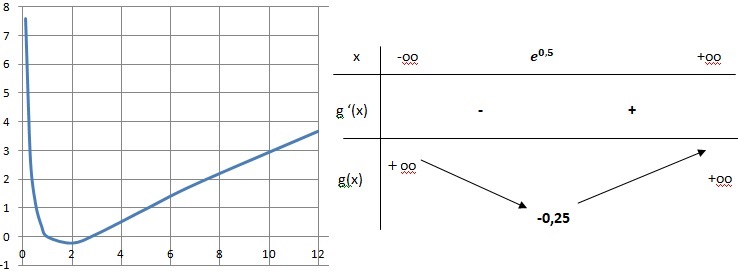3. Dresser le tableau de variations de la fonction g sur l’intervalle ]0 ; +∞[. On fera figurer dans ce tableau les limites de la fonction g en 0 et en +∞, ainsi que la valeur du minimum de g sur ]0 ; +∞[. 4. Démontrer que, pour tout nombre réel m > −0,25, l’équation g(x) =m admet exactement deux solutions. D'après le tableau de variations ci-dessus, g(x) > -0,25. g(x) est strictement décroissante sur ]0 ; e0,5[ de +oo à -0,25 et g(x) est strictement croissante sur ] e0,5 : +oo[  de -0,25 à +oo. Pour tout nombre réel m > −0,25, l’équation g(x) =m admet donc exactement deux solutions. 5. Déterminer par le calcul les deux solutions de l’équation g(x) = 0. ln(x) ( ln(x)-1)=0. ln(x) = 0 soit x = 1. ln(x)-1=0 ; ln(x) = 1 soit x = e.

menu