De
la musique dans le calme, atténuation, interférences, bac SI Métropole
2021.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
..
..
|
.
.
|
..
..
......
...
|
Partie 1.
Un
musicien s'entraîne sur sa guitare électrique. Il se trouve à une
distance d = 1,0 m du haut parleur, considéré comme une source de
puissance constante émettant de façon équivalente dans toutes les
directions. Il utilise un sonomètre et mesure un niveau d'intensité
sonore L1 = 85 dB. Il aimerait réduire son exposition au bruit.
1. Citer deux options qui s'offrent à lui.
Utiliser un casque anti-bruit actif.
S'éloigner du haut-parleur : l'intensité sonore est inversement
proportionnelle au carré de la distance. Quand la distance double, le
niveau sonore diminue de 6 dB.
Il décide de s'éloigner du haut-parleur.
2. Calculer l'intensité sonnore I1 associée au niveau sonore L1.
L1 = 10 log (I1/I0).
I1 = I0 100,1 L1 = 10-12 x 108,5 = 10-3,5 =3,2 10-4 W m-2.
3. A quelle distance doit-il se placer pour être exposé à un niveau sonore L2 = 75 dB ?
I2 = I0 100,1 L2 = 10-12 x 107,5 = 10-4,5 =3,2 10-5 W m-2.
I2 / I1 = 0,10.
I2/I1 = (d1/d2)2 = 0,10 avec d1 = 1,0 m.
d2 2=10 ; d2 ~3,2 m.
Partie 2.
Le musicien fait l'acquisition d'un casque antibruit actif. Le casque
détecte les ondes sonores entrant dans le casque et émet une autre onde
sonore en même temps. Dans certaines conditions, le porteur entend un
son atténué.
Une simulation de l'enregistrement du son au niveau de l'oreille du musicien est proposée.
4. Justifier que le son est audible par l'homme.
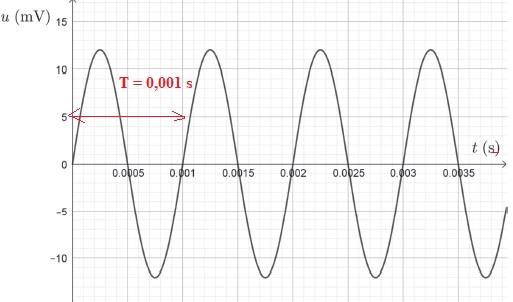
Fréquence f = 1 /T = 1 /0,001 = 1000 Hz, audible par l'homme.
5. Tracer
la représentation du signal que devrait émettre le casque pour que le
porteur n'entende pas de son. Nommer le phénomène mis en jeu.
Interférences destructives.
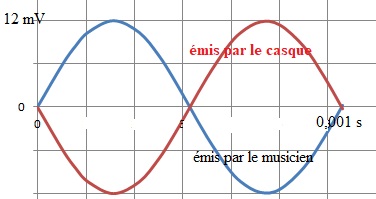
Cette
"annulation" du son rappelle une expérience à notre guitariste : en se
plaçant entre deux haut-parleurs, le son entendu peut-être fortement
atténué pour certaines positions de l'auditeur. Les haut-parleurs étant
branchés à la même source, ils émettent en phase.
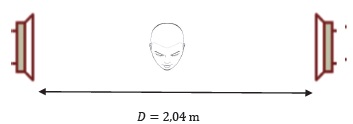
Le
musicien se place initialement à égale distance des haut-parleurs. La
taille de sa tête n'est pas prise en compte et la fréquence des deux
signaux est de 1000 Hz.
6. Justifier que le son qu'il entend a une intensité maximale.
La différence de marche est nulle : les interférences sont constructives.
7. Déterminer de quelle distance minimale doit se déplacer le musicien pour que le son entendu ait une intensité minimale.
Longueur d'onde l =c / f = 340 / 1000 =0,34 m.
Les interférences doivent être destructives : la différence de marche
doit être un multiple impair de la demi-longueur d'onde soit 17 cm.
On note x la distance du musicien par rapport au haut-parleur de droite et 2,04-x celle par rapport au haut-parleur de gauche.
Différence de marche : 2,04-x-x= 0,17 ; x =0,935 m.
Position initiale du musicien 1,02 m.
Il doit se déplacer de 1,02 -0,935 =0,085 m.
|


