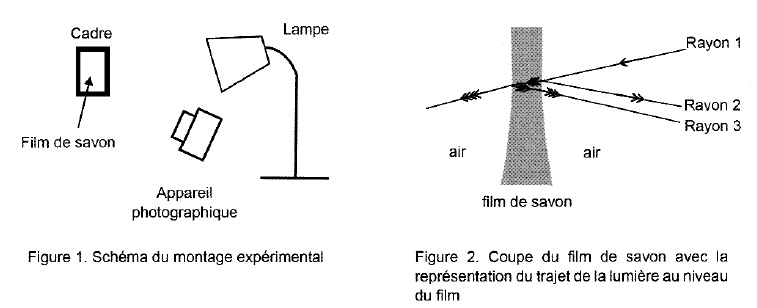
Etude d'un film de savon, interférences lumineuses, bac Métropole 2021. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. .. .. . . .. .. ...... ... Un cadre de forme rectangulaire est plongé dans  de l'eau savonneuse pour former un film de savon à l'intérieur du cadre. L'épaisseur du film n'est pas la même partout : elle est plus importante en bas du dispositif du fait de la gravité. On éclaire ce film avec de la lumière blanche et sous un angle approprié, on observe une figure d'interférences. Le rayon 1 arrive sur le film. La lumière est en partie réfléchie ( rayon 2) et elle pénètre en partie dans le film. Le rayon issu de la réflexion sur l'autre côté du film en ressort ( rayon 3). Les rayons 2 et 3 interfèrent. les interférences sont visibles sur le film de savon. Indice de réfraction du film de savon n = 1,34 pour toutes les longueurs d'onde. 1. Le phénomène d'interférences. Ce film est photographié et l'image est traitée par un logiciel qui permet de sélectionner une couleur correspondant à la longueur d'onde l dans l'air égale à 600 nm. 1.1. Comment distinguer les zones où les interférences sont constructives de celles où les interférennces sont destructives ? Interférences constructives : zones blanches. Interférences  destructives : zones noires. 1.2 Donner la condition d'interférences constructives et celle d'interférences destructives. Interférences constructives : la différence de marche est un multiple de la longueuur d'onde. Interférences destructives : la différence de marche est un multiple impair de la demi-longueuur d'onde. 1.3 Sur la figure suivante, on a représennté le film de savon dans le cas où la lumière arrive perpendiculairement à sa surface. Au voisinage de M, on considère que les deux  faces du film sont parallèles et que son épaisseur est e = 900 nm. On admet que la différence de chemin optique au point M entre les rayons 2 et 3 a pour expression : d(M) = 2ne-½l. Déterminer si les interférences  au point M sont destructives ou constructives. d(M) =2 x1,34 x900 -0,5 x600=2112 nm 2112 ~7 x(½l). Les interférences sont destructives en M. ... .... 2. Comparaison du phénomène d'interférences suivant la longueur d'onde étudiée. La photo de l'expérience est traitée à l'aide d'un logiciel pour réaliser l'étude du phénomène en lumière bleue ( 458 nm) et  en lumière rouge-orangée ( 600 nm). En raison des phénomènes de réflexion des rayons, les interférences constructives apparaissent pour différentes épaisseurs du film de savon. 2.1. Montrer que les épaisseurs correspondant à des interférennces constructives sont données par : ek = (2k+1)/ 4 l / n. n : indice  de réfraction du film ; ek épaisseur du film ; l : longueur d'onde dans l'air. d(M) = 2nek-½l = k l avec k entier. 2nek = l(k+0,5). ek = l(k+0,5) /  (2n) = (2k+1)/ 4 l / n. 2.2. Calculer l'épaisseur minimale pour que des interférences constructives apparaissent en lumière bleue. k = 1 ; e =0,75 x 458 /1,34 ~ 256 nm. 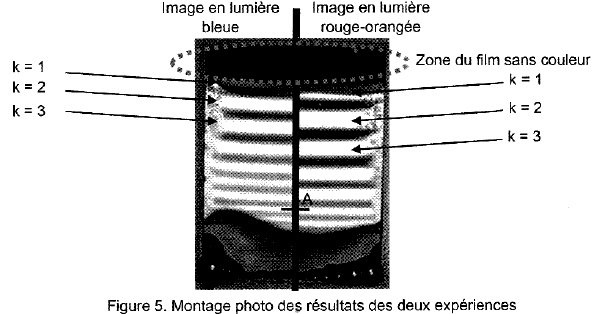2.3. La zone sans couleur correspond à une épaisseur du film très faible. On obtient alors des interférennces destructives. On observe qu'au cours du temps la surface de cette zone s'étend vers le bas. Proposer une explication. Du fait de la gravité, le film est de plus en plus mince dans la partie supérieure et de plus en plus épais dans la partie inférieure. 2.4. Au niveau du point A, on observe des interférences constructives à la fois en lumière bleue et en lumière rouge-orangée. Déterminer l'épaisseur du film au point A. ek = (2k+1)/ 4 lbleu / n avec k = 8 ( d'après la figure 5 ). ek =17 / 4 x458 / 1,34 =1452 nm ~1,45 103 nm. ek' = ek= (2k'+1)/ 4 lrouge / n  avec k = 6 ( d'après la figure 5 ). ek =13 / 4 x 600 / 1,34 =1455 nm ~1,45 103 nm.

menu