Saut à l'élastique, bac Métropole 2021.

Le saut se déroule en trois phases.
Phase 1 : chute libre, élastique non tendu.
Phase 2 : l'élastique se tend, le sauteur ralentit. Il s'arrête quand l'élastique est complétement étiré.
Phase 3 : l'élastique se contracte, le sauteur remonte en reprenant de la vitesse puis en ralentissant à nouveau.
Ces trois phases se répètent jusqu'à ce que le sauteur soit immobile. La durée du saut est de l'ordre d'une minute.
La saut est éffectué à partir d'un pont situé à une hauteur H = 50 m au dessus du sol.
Longueur de l'élastique non étiré : L₀ = 8,0 m.
Phase 1. On suppose que le mouvement est vertical. Vitesse initiale du sauteur v₀.
Le référentiel d'étude est le référentiel terrestre. L'axe Oz est vertical, dirigé vers le haut, l'origine est au sol.
1. Déterminer les coordonnées du vecteur accélération.
La chute est libre : a = -g.
2 Etablir que l'équation horaire du mouvement est z = -½gt² -v₀t +H.
Le vecteur vitesse est une primitive du vecteur accélération et la vitesse initiale est v₀, verticale orientée vers le bas.
v = -gt -v₀.
La position est une primitive du vecteur vitesse et la position initiale est H.
z = -½gt² -v₀t +H.
3. Après traitement de la vidéo d'un saut, on obtient l'équation horaire suivante :
z = -4,9 t²-1,10 t +49,8.
Cette modélisation est'elle cohérente avec l'expression précédente ?
Oui : -4,9 correspond à -½g ;
La hauteur du pont 50 m est proche de 49,8 m ;
La vitesse initiale est faible et orientée vers le bas.
4. Calculer la date à laquelle l'élastique commence à se tendre.
z =49,8- 8,0 =41,8 m.
41,8 = -4,9 t² -1,10 t+49,8.
4,9 t² +1,10 t-8=0.
Discriminant D =1,1² +4*8*4,9 =158,01 ~12,57².
Racine positive retenue : (-1,10+12,57) / 9,8 =1,17 ~1,2 s..
5. En déduire la vitesse à cet instant.
|v| =| -9,8x1,2 -1,1| =12,6 ~13 m /s.
6. Lors du saut, les différentes énergies sont représentées ci-dessous. L'énergie potentielle de pesanteur est prise égale à zéro au sol. Pour une de ces énergies, les calculs n'ont pu être effectués que sur la première phase du saut ( courbe A).

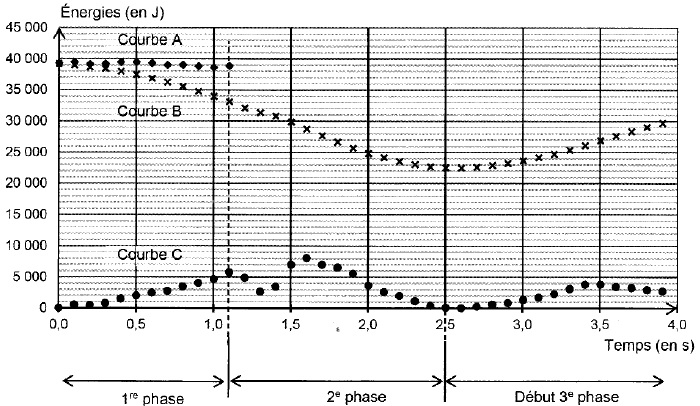
6.1. Identifier chaque courbe en justifiant.
A : au cours d'une chute libre l'énergie mécanique se conserve.
B : l'énergie potentielle de pesanteur diminue jusqu'à ce que l'élastique soit complètement étiré, puis augmente ensuite.
C. L'énergie cinétique croît, puis diminue quand l'élastique commence à se tendre. Elle s'annule quand l'élastique est complètement étiré.
6.2. Identifier l'(les) informations manquante(s) sur le système physique étudié nécessaire au tracé de la suite de la courbe A.
La raideur de l'élastique.
6.3 Pour des raisons de sécurité, l'élastique est choisi tel que son étirement DL soit inférieur ou égal à 4 L₀. Calculer la distance maximale parcourue par le sauteur. Conclure.
Etirement maximal : 4 x8 = 32 m.
Distance maximale parcourue : 32 +8 = 40 m.
Cette valeur étant inférieure à 50 m, le sauteur ne s'écrase pas au sol.