Mathématiques
: QCM, probabilités, fonction, suite, géométrie, bac Métropole 2021.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
..
..
|
.
.
|
..
..
......
...
|
Exercice
1. QCM. 4 points.
On considère :
- la droite D passant par les points A(1 ; 1 ; -2) et B(-1 ; 3 ; 2) ;
- La droite D' de représentation paramétrique :
x = -4+3t ; y = 6-3t ; z = 8-6t avec t réel ;
- le plan P d'équation cartésienne x+my-2z+8=0 avec m un réel.
1. Parmi les points suivants, lequel appartient à la droite D' ?
M1(-1 ; 3 ; -2) ; M2(11 ; -9 ; -22) vrai ; M3(-7 ; 9 ; 2) ; M4(-2 ; 3 ; 4).
M1 : -1 = -4+3t ; t=1 ; y =6-3=3 ; z=8-6=2 diffère de -2.
M2 : 11 = -4+3t ; t=5 ; y =6-15=-9 ; z=8-30= -22 .
y = 6-3t ; z = 8-6t
2. Coordonnées d'un vecteur directeur de la droite D' :
(-4 ; 6 ; 8) ; (3 ; 3 ; 6) ; (3 ; -3 ; -6) vrai ; (-1 ; 3 ; 2).
3. Les droites D et D' sont :
sécantes ; strictement parallèles ; non coplanaires ; confondues. Vrai
xA = -4+3t =1 soit t = 5 /3 ; y = 6-5=1= yA ; z = 8-10 =-2 = zA.
xB = -4+3t = -1 soit t = 1 ; y = 6-3=3= yB ; z = 8-6 = 2 = zB.
4. La valeur de m pour laquelle la droite D est parallèle au plan P est :
-1 ; 1 ; 5 vrai ; -2.
Coordonnées d'un vecteur directeur de la droite D : (-2 ; 2 ; 4).
Coordonnées d'un vecteur normal au plan P : (1 ; m ; -2).
Si la droite D et le plan P sont parallèles, le produit scalaire de ces deux vecteurs doit être nul :
-2*1+2m-2*4=0 soit m =5.
Exercice 2. ( 6
points).
La
leucose des chats est provoquée par un virus. Dans un centre
vétérinaire, on estime que 40 % des chats sont porteurs de la maladie.
On réalise un test de dépistage de la maladie parmi les chats présents
dans ce centre. Les caractéristiques du test sont :
- lorsque le chat est porteur de la maladie, le test est positif dans 90 % des cas ;
- lorsque le chat n'est pas porteur de la maladie, le test est négatif dans 85 % des cas.
On choisit un chat au hasard et on considère les événements suivants :
M : le chat porte la maladie.
T : le test est positif.
1.a Traduire la
situation à l'aide d'un arbre pondéré.
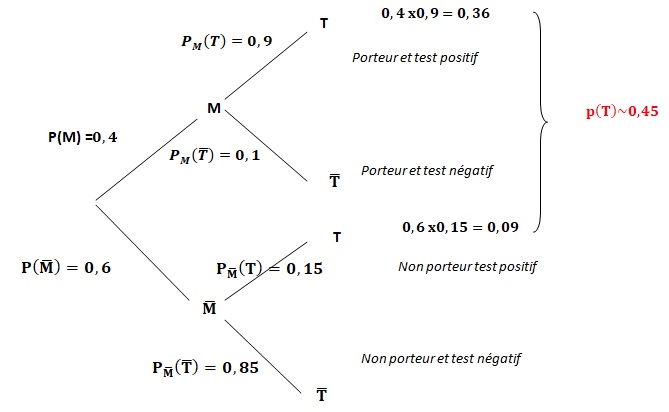
1.b Calculer la probabilité que le chat porte la maladie et que le test soit positif.
P(M n T)=0,4 x0,9 = 0,36.
c. Démontrer que
P(T) = 0,45.
d. On choisit un chat parmi ceux dont le test est positif. Clalculer la probabilité qu'il porte la maladie.
P(T(M) = P(T n M) / P(T) =0,36 / 0,45=0,80.
2. Dans ce centre, on choisit un échantillon de 20 chats au hasard.
On note X la
variable
aléatoire qui donne le nombre de chats présentant un test positif dans cet
échantillon.
a. Justifier que X
suit une loi binomiale et déterminer les paramètres de cette loi.
On
choisit 20 chats de manière indépendante. Deux issues sont possibles "
le test est positif " ou" le test est négatif".
On
répète 20 fois une épreuve de Bernoulli.
X
suit une loi binomiale de paramètre n =20 ; p = 0,45.
b. Calculer la probabilité que cet
échantillon contienne exactement 5 chats présentant un test positif.
P (X =5)
= 0,0365.
c. Calculer la probabilité que cet
échantillon contienne au plus 8 chats présentant un test positif.
P (X < 8)
= 0,414.
d. Calculer
l'espérance de la variable X et interpréter.
E = np = 20 x0,45 = 9.
En moyenne, chaque échantillon contient 9 chats donnant un test positif.
3. On choisit un échantillon de n chats dans le centre. On note pn la probabilité qu'il y ait au moins un chat présentant un test positif dans cet échantillon.
a. Montrer que pn = 1-0,55n.
pn = 1-P(X=0) =1- Cn0 0,450 x0,55n =1-0,55n.
b. Décrire le rôle du programme suivant :(n entier naturel et p un réel).
def seuil()
n=0
p=0
while p < 0.99 :
n = n+1
p = 1-0,55**n
return n
Ce programme donne la taille de l'échantillon : la probabilité de
trouver au moins un chat donnant un test positif doit étre
supérieure à 0,99.
c. Déterminer la valeur renvoyée par ce programme.
1-0,55n=0,99 ; 0,01=0,55n ; n = ln(0,01) / ln(0,55) ~7,7 soit 8.
|
...
|
....
|
Exercice 3. (5 points).
On considère la suite (un) définie par u0 = 1 et un+1 = 4 un / (un+4).
n
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
un
|
1,00
|
0,80
|
0,67
|
0,57
|
0,50
|
0,44
|
0,40
|
0,36
|
0,33
|
0,31
|
0,29
|
4 / un
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
14
|
1. Conjecturer l'expression 4 / un en fonction de n.
4 / un =4+n.
2. Démontrer par récurence que un >0.
Initialisation : u0=1 >0, la propriété est vraie au rang 0.
Hérédité : la propriété est supposée vraie au rang n : un >0.
4 un et (un+4) sont positifs ;
4 un / (un+4) >0 ; donc un+1 >0.
La propriété est vraie au rang n+1.
Conclusion : la propriété est vraie au rang zéro et héréditaire ; donc elle est vraie pour tout n.
3. Démontrer que cette suite est décroissante.
un+1-un = 4 un / (un+4) -un = (4un-un2-4un) / (un+4) = -un2 / (un+4) < 0.
un+1< un : la suite est décroissante.
4. Que peut on conclure des questions 3 et 4 concernant cette suite ?
Cette suite est décroissante et bornée, donc elle converge.
5. On considère la suite (vn) définie par vn = 4 / un.
Démontrer que cette suite est arithmétique. Exprimer vn en fonction de n.
vn+1=4 / un+1 = (un+4) / un = 1+4/un = 1 +vn.
La suite (vn) est arithmétique de raison 1 et de premier terme v0 = 4.
vn = 4 +n.
6. Exprimer un en fonction de n. En déduire la limite de la suite (un).
un = 4 / vn = 4 / ( 4+n).
Quand n tend vers plus l'infini, un tend vers zéro.
Exercice A ( Fonction logarithme ).
Partie I.
On désigne par h la fonction définie sur ]0 ; +oo[ par : h(x) = 1+ln(x) / x2.
1. Déterminer les limites de h en zéro et en plus l'infini.
En zéro, ln(x) tend vers -oo ; ln(x) / x2 tend vers - oo.
h(x) tend vers moins l'infini quand x tend vers zro.
En plus l'infini, par croissance comparée, ln(x) / x2= 0,5 ln(x2) / x2, tend vers zéro.
h(x) tend vers 1 quand x tend vers plus l'infini.
2. Montrer que h '(x) =(1-2ln(x)) / x3.
On pose u = ln(x) et v = x2.
u' = 1 /x ; v' = 2x.
(u'v-v'u) / v2 =(x-2xln(x)) / x4 = =(1-2ln(x)) / x3.
3. En déduire les variations de h(x).
h'(x) =0 si ln(x) = 0,5 soit x = e0,5.
Si x appartient à ]0 ; e0,5[, h'(x) >0 et h(x) est croissante.
Si x > e0,5, h'(x) < 0 et h(x) est décroissante.
4. Montrer que h(x) = 0 admet une solution unique a tel que 0,5 < a < 1.
Sur ]0,5 ; 1), h(x) est strictement croissante.
Quand x = 0,5, h(0,5)~ -1,77.
h(1 ) =1.
h(x) = 0 admet une solution unique a tel que 0,5 < a < 1.
5. Déterminer le signe de h(x) sur ]0 ; +oo[.
Si x appartient à ]0 ; a[, h(x) < 0.
Si x appartient à ]a ; +oo[, h(x) > 0.
Partie II.
On désigne par f1 et f2 les fonctions définies sur ]0 ; +oo[ par :
f1=x-1-ln(x) / x2 et f2 =x-2-2ln(x) / x2 .
On note C1 et C2 leurs courbes représentatives.
1. Montrer que h(x) = f1(x) -f2(x).
x-1-ln(x) / x2 -(x-2-2ln(x) / x2 ) = 1+ln(x) / x2 = h(x).
2. En déduire la position relative des courbes C1 et C2. Justifier que leur unique point d'intersection a pour coordonnées ( a ; a).
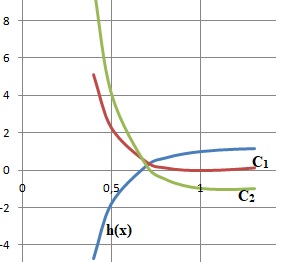
Si x appartient à ]0 ; a[ : h(x) < 0 ; f1(x) < f2(x) et C2 est au dessus de C1.
Si x appartient à ]a ; +oo[ : h(x) > 0 ; f1(x) > f2(x) et C1 est au dessus de C2.
Coordonnées de leur point d'intersection :
x-1-ln(x) / x2 =x-2-2ln(x) / x2 .
0= -1-ln(x) / x2 ; solution x = a.
f1(a)=a-1-ln(a) / a2 =a.
Exercice B ( fonction exponentielle )
On donne la courbe représentant la fonction dérivée f ' d'une fonction f. Conjecturer à l'aide de la courbe :
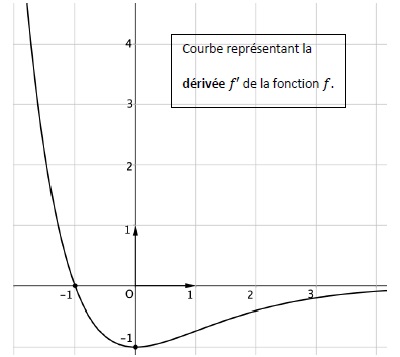
1. Le sens de variation de f sur R.
Sur ]-oo ; -1[, f '(x) >0 et f(x) strictement croissante.
Sur ]-1 ; +oo[, f '(x) < 0 et f(x) strictement décroissante.
f(x) présente un maximum en x = -1.
2. La convexité de la fonction f.
f(x) est concave sur ]-oo ; 0[ et convexe sur ]0 ; +oo[..
On admet que f(x) = (x+2)e-x. On note C sa courbe représentative.
1. Montrer que f(x) =x /ex +2e-x. En déduire sa limite en plus l'infini. Justifier que C admet une asymptote que l'on précisera.
f(x) = xe-x+2e-x= x /ex +2e-x.
Par croissance comparée, x /ex tend vers zéro quand x tend vers +oo.
e-x tend vers zéro quand x tend vers +oo.
f(x) tend vers zéro quand x tend vers +oo.
La droite d'équation y =0 est asymptote à C.
2.a Montrer que f '(x) = -(x+1)e-x.
On pose u = x+2 ; v = e-x ; u' = 1 ; v' = -e-x.
u'v +v'u = e-x-(x+2)e-x=e-x(-1-x).
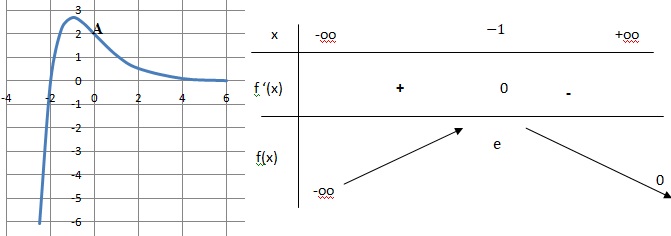
b. Etudier les variations de f et dresser son tableau de variation.
e-x> 0 ; le signe de f '(x) est celui de -1-x.
Si x = -1; f '(x) =0.
Si x < -1, f '(x) >0 et f(x) croissante.
Si x > -1, f '(x) <0 et f(x) décroissante.
f(x) présente un maximum en x = -1.
c. Montrer que f(x) = 2 admet une solution unique sur [-2 ; -1] dont on donnera une valeur approchée.
Sur [-2 ; -1], f(x) est strictement croissante.
f(-2) = 0 ; f(-1)=e > 2.
f(x) = 2 admet donc une solution unique sur [-2 ; -1].
f(-1,6) ~2.
3. Déterminer f '' (x) et étudier la convexité de la fonction f. Que représente pour la courbe C le point A d'abscisse 0 ?
On pose u = -1-x et v = e-x.
u' = -1 ; v' = -e-x ; u'v+v'u = -e-x+e-x(1+x) = xe-x.
Si x < 0, f ''(x) < 0, la courbe C est concave.
Si x > 0, f ''(x) > 0, la courbe C est convexe.
f''(x) s'annule et change de signe en x=0. A est un point d'inflexion de la courbe C.
|
|



