Mission sur la lune, bac Métropole 2021. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. .. .. . . .. .. ...... ... Décollage depuis la terre de la mission Apollo 11. La fusée Saturn V est composée de 3 étages contenant du carburant. Lorsqu'ils sont vides, ces étages se décrochent au fur et à mesure de la progression de la fusée. Elle met en orbite le vaisseau Apollo 11 qui effectue 1,5 tour autour de la terre. Ce vaisseau est ensuite transféré sur une nouvelle trajectoire qui va le mener à proximité de la lune. L'étude est effectuée dans le référentiel géocentrique supposé galiléen. Vitesse du vaisseau Apollo 11 sur son orbite circulaire de rayon r = 6,56 103 km ; v =7,79 103 m /s. 1.1 Calculer la valeur de la durée passée en orbite terrestre par l'équipage dans  le vaisseau Apollo 11. Circonférence de l'orbite circulaire : 2 p r = 6,28 x 6,56 106 =4,12 107 m. 1,5 tours = 1,5 x4,12 107 =6,18 107 m. Durée = 6,18 107  / (7,79 103) =7,94 103 s ( ~2 h 12 min). 1.2. L'énergie potentielle de pesanteur du vaisseau Apollo 11 en orbite terrestre est Ep = -2,74 1012 J, l'origine de cette énergie étant prise nulle à grande distance de la terre. 1.2.1  Calculer l'énergie cinétique du vbaisseau en orbite. Ec = ½mv2 avec m =4,50104 kg. Ec = 0,5 x 4,50 104 x(7,79 103)2=1,37 1012 J. 1.2.2. En déduire l'énergie mécanique de ce vaisseau. Em = Ep+Ec =(-2,74 +1,37) 1012 = - 1,37 1012 J. 1.3. La valeur de l'énergie mécanique Em0 de ce vaisseau avant le décollage est -2,81 1012 J. 1.3.1. Déterminer l'énergie minimale que doit fournir Saturn V pour mettre en orbite le vaisseau Apollo 11. Conclure, sachant que la fusée est un lanceur qui a la capacité de fournir une énergie de l'ordre de  5 1012 J pour mettre un corps en orbite autour de la terre. Em0 + E fournie = Em. E fournie = Em -Em0 = (-1.37 +2,81)1012=1,44 105 J, valeur inférieure à 5 1012. 1.3.2. Expliquer pourquoi l'énergie cinétique du vaisseau avant le décollage n'est pas nulle dans le référentiel géocentrique. Dan s ce référentiel, un point de la surface de la terre n'est pas immobile du fait de la rotation de la terre sur elle même. 2. M. Collins en orbite autour de la lune. Apollo 11 se trouve au voisinage de la lune à une altitude hL = 110 km par rapport au sol lunaire. le module lunaire se détache du vaisseau emportant à son bord deux astronautes vers le sol lunaire. Le troisième reste seul en orbite dans le vaisseau qui est animé d'un mouvement supposé circulaire uniforme dans le référentiel d'étude centré sur la lune et supposé galiléen. Libéré de son module la masse du vaisseau est m = 3,0 104 kg environ. Les deux astronautes restent 21 h 36 min sur le sol lunaire. 2.1 et 2. Déterminer l'expression du vecteur accélération du vaisseau en orbite lunaire ainsi que la norme de sa vitesse. 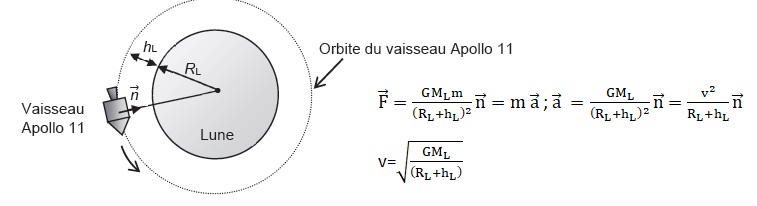ML = 7,34 1022 kg ; RL = 1,73 106 m. v = ( 6,67 10-11 x7,34 1022/ (1,73 106 +1,1 105)) ½ =1,63 103 m /s. 2.3 Calculer la valeur de la période de révolution T du vaisseau Apollo 11, puis déterminer celle du nombre de tours autour de la lune qu'à fait l'astronaute pendant le séjour des deux autres sur la lune. Circonférence : 2p(RL+hL)=1,156 107 m. Période T = 1,156 107 /( 1,63 103) =7,093 103 ~7,1 103 s ~1,97 heures. Nombre de tours : 21 h 36 min = 21,6 heures. 21,6 / 1,97 ~ 11 tours. ... .... 3. Saut de John Young lors de la mission Apollo 16. L'astronaute a fait un grand saut vertical, ses pieds étant situés à 60 cm au dessus du sol. On choisit l'axe vertical Oy orienté vers le haut, l'origine O de cet axe étant au niveau du sol lunaire. La courbe suivante représente l'évolution de la position de J. Young en fonction du temps pendant son saut. Lorigine des dates est prise au début du saut. 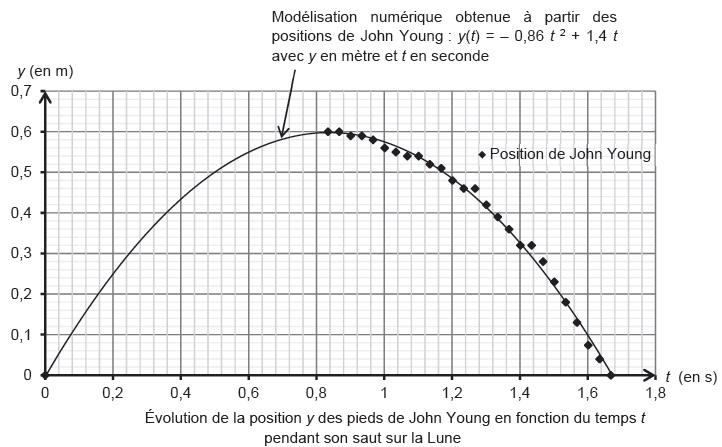En absence d'atmosphère sur la lune, le saut est une chute verticale. 3.1. Déterminer l'exppression numérique de la vitesse vy(t) de J. Young. Calculer la valeur initiale de cette vitesse. y(t) = -0,86 t2 +1,4t. vy(t) = dy(t) / dt = -1,72 t+1,4. vy(0) =1,4 m /s. 3.2.  Montrer que la valeur de l'intensité de la pesanteur sur la lune est gL ~1,7 m s-2. y(t) = -0,5 gL t2 +vy(0)t. y(t) = -0,86 t2 +1,4t. On identifie : gL = 2 x0,86 ~,7 m s-2. 3.3. J.Young avec son scaphandre a une masse totale m = 150 kg et il parvient cependant à faire un saut vertical de 60 cm sur la lune. Déterminer les valeurs de la hauteur et de la durée d'un saut vertical qu'aurait réalisé J. Young avec son équipement sur la terre avec la vitesse initiale v0y dans le cadre du modèle de chute libre. Commenter.  Energie cinétique  initiale: ½mv0y2 =0,5 x 150 x1,42 =147 J. Energie mécanique initiale 147 J, en prenant l'origine de l'énergie potentielle de pesanteur au sol. L'énergie mécanique se conserve : Au point le plus haut, l'anergie cinétique est nulle. 147 = m g h = 150 x9,81 h ; h = 0,10 m. ( Un saut de puce ).

menu