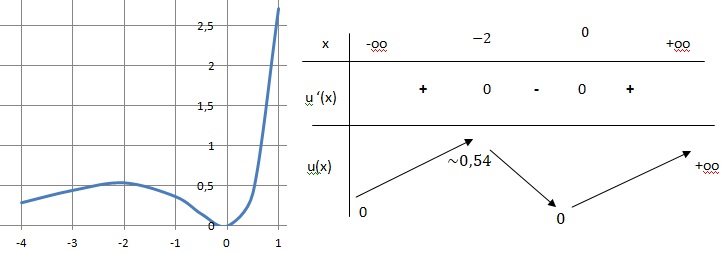Mathématiques
: QCM, probabilités, fonction, suite, géométrie, bac Métropole 2021.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
..
..
|
.
.
|
..
..
......
...
|
Exercice
1. QCM. 4 points.
Soit la fonction f définie sur [0 ; +oo[ par : f(x) = e2x /
x.
On donne la dérivée seconde f "(x) =2e2x(2x2-2x+1)
/x3.
1. La fonction f ',
dérivée de f est définie par :
2e2x ; e2x(x-1) /x2 ; e2x(2x-1)
/x2 vrai ; e2x(2x+1)
/x2 .
On pose u = e2x ; v = x ; u' = 2 e2x ; v' = 1.
(u'v-v'u) / v2 =(2x e2x -e2x) / x2
=e2x(2x-1)
/x2 .
2. La fonction f :
est décroissante ;
est monotone ;
admet un minimum en 0,5 ; vrai
admet un maximum en
0,5.
Etude du signe de la dérivée : e2x /x2 >0.
Le signe de la dérivée est celui de 2x-1.
f '(x) = 0 si x = 0,5.
f '(x) > si x > 0,5 ; f (x) croissante.
f '(x) < 0 si x < 0,5 et f(x) décroissante.
3. La fonction f
admet pour limite en plus l'infini.
+oo vrai ; 0 ; 1 ; e2x.
Par croissance comparée e2x / x tend vers plus l'infini
quand x tend vers plus l'infini.
4. La fonction f est :
concave
sur ]0 ; +oo[ ;
convexe sur ]0 ; +oo[ ; vrai.
concave sur ]0 ;
0,5[ ;
est représentée par une courbe présentant un point d'inflexion.
f
"(x) =2e2x(2x2-2x+1) /x3 .
Etude du signe de la dérivée seconde.
2e2x/x3 positif sur ]0
; +oo[ ;
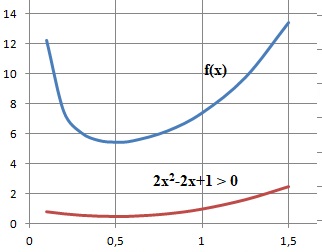
Etude du signe de 2x2-2x+1 :
Discriminant D =
(-2)2-4*2 = -4, aucune racine réelles.
2x2-2x+1 >0.
La dérivée seconde étant positive, la fonction f(x) est convexe.
Exercice 2. ( 5
points).
Une chaîne de fabrication produit des pièces mécaniques. On estime que
5 % des pièces sont défectueuses.
Un test mis au point a deux résultats possibles : positif ou bien
négatif.
On applique ce test à une pièce choisie au hasard dans la production.
On note les événements suivants :
D : pièce défectueuse.
T : test positif.
La probabilité qu'une pièce présente un test positif sachant qu'elle
est défectueuse est 0,98.
La
probabilité qu'une pièce présente un test négatif sachant qu'elle n'est
pas défectueuse est 0,97.
Partie1.
1. Traduire la
situation à l'aide d'un arbre pondéré.
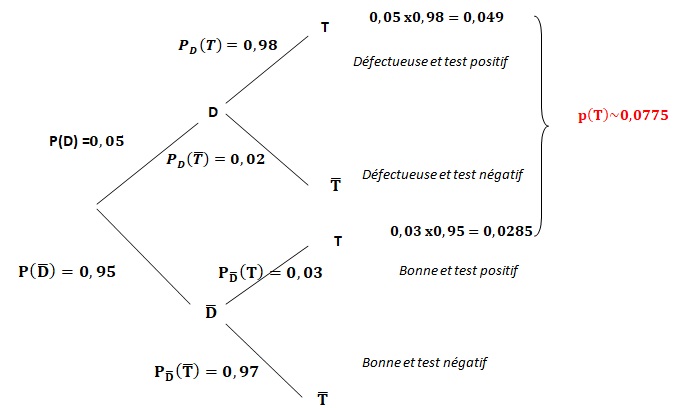
2.a Déterminer la
probabilité qu'une pièce choisie au hasard soit défectueuse et présente
un test positif.
b. Démontrer que
P(T) = 0,0775.
3.
On appelle valeur prédictive positive du test la probabilité qu'une
pièce soit défectueuse sachant que le test est positif. Pour être
efficace un test doit avoir une valeur prédictive positive supérieure à
0,95.
Calculer cette valeur prédictive positive. Le test est-il efficace ?
PT(D) =P(T n D) / P(T) = 0,049 / 0,0775 ~0,63 < 0,95.
Le test n'est pas efficace.
Partie
II.
On choisit un échantillon de 20 pièces. On note X la
variable
aléatoire qui donne le nombre de pièces défectueuses de cet
échantillon. On rappelle que p(D) = 0,05).
1. Justifier que X
suit une loi binomiale et déterminer les paramètres de cette loi.
On
choisit 20 pièces de manière indépendante. Deux issues sont possibles "
la pièce est bonne " ou" la pièce est défectueuse".
On
répète 20 fois une épreuve de Bernoulli.
X
suit une loi binomiale de paramètre n =20 ; p = 0,05.
2. Calculer la probabilité que cet
échantillon contienne au moins une pièce défectueuse.
P (X > 1)
=1-P(X=0) = 1-0,358 =0,642.
3. Calculer
l'espérance de la variable X et interpréter.
E = np = 20 x0,05 = 1.
En moyenne, chaque échantillon contient une pièce défectueuse.
|
...
|
....
|
Exercice 3. (6 points).
Cécile sort les gâteaux du congelateur à -19°C et les apporte sur la
terrasse où la température est 25°C.
Au bout de 10 minutes la température des gâteaux est1,3 °C.
I. Premier modèle.
On suppose que la vitesse de décongelation des gâteaux est constante,
c'est à dire que l'augmentation de la température est lamême minute
après minute.
Selon ce modèle, déterminer la température des gâteaux 25 minutes après
la sortie du congelateur. Ce modèle est-il pertinent ?
En 10 minutes, la température des gâteaux augmente de 20,3 °C, soit
2,03 °C par minute.
Selon ce modèle, la température des gâteaux serait de -19 +2,03 x25 =
-19 +50,75 =31,75 °C.
Impossible, la température finale des gâteaux ne peut pas dépasser la
température ambiante 25°C.
Second modèle.
On note Tn la température des gâteaux au bout de n minutes
après leur sortie du congélateur. T0 = -19°C.
L'évolution de la température est donnée par : Tn+1- Tn
= -0,06 (Tn-25).
1. Justifier
que Tn+1 = 0,94 Tn +1,5.
Tn+1= Tn
-0,06 Tn+0,06 x25.
Tn+1 = 0,94 Tn
+1,5.
2. Calculer T1
et T2.
T1 = 0,94 T0+1,5 = -0,94 x 19 +1,5 =-16,36 ~-16,4
°C.
T2 = 0,94 T1+1,5
= -0,94 x 16,36 +1,5 =-13,88 ~-13,9 °C.
3. Démontrer par récurrence que Tn
< 25.
Initialisation
: T1 = -16,4, la propriété est vraie au rang 1.
Hérédité :
la propriété est supposée vraie au rang n.
Tn < 25.
Tn+1 = 0,94 Tn
+1,5.
Tn+1 < 25.
Conclusion
: la propriété est vraie au rang 1 et héréditaire, elle est vraie pour
tout entier n.
Cette situation est prévisible, la température des gâteaux ne peut pas
dépasser la température ambiante.
4.
Etudier le sens de variation de cette suite.
Tn+1- Tn
= -0,06 (Tn-25) avec Tn < 25.
-0,06 (Tn-25) est
donc positif ou nul.
Tn+1- Tn
> 0,la
suite est croissante.
5. Démontrer
que cette suite est convergente.
Cette suite est croissante et bornée par 25, donc elle converge.
6. On pose pour tout entier n, Un
= Tn-25.
a. Montrer que (Un) est
une suite géométrique dont on précisera la raison et le premier terme.
Un+1 = Tn+1-25.
Tn+1 = 0,94 Tn
+1,5.
Un+1 =0,94 Tn
+1,5 -25.
Un+1 =0,94 Tn
-23,5.
Un+1 = 0,94(Tn-25) = 0,94 Un.
(Un) est une
suite géométrique de raison 0,94 et de premier terme :
U0 = T0-25 = -19-25 = -44.
b. En déduire que Tn =
-44 x0,94n+25.
Un = -44 x0,94n.
Un = Tn-25.
Tn = Un+25.
Tn = -44 x0,94n+25.
c. En déduire la limite de (Tn).
-1 < 0,94 < 1, donc 0,94n
tend vers zéro quand n tend vers plus l'inifini.
(Tn) tend vers 25, la température ambiante.
7.a Le fabricant
conseille de consommer les gâteaux au bout d'une demi-heure à
température ambiante après leur sortie du congelateur. Quelle est alors
la température des gâteaux ?
n = 30 ; T30 =-44 x0,9430 +25 ~18°C.
b. Cécile aime
déguster ces gâteaux à la température de 10°C. Donner un encadrement
entre deux entiers consécutifs du temps en minutes après lequel Cécile
doit déguster son gâteau.
-44
x0,94n+25 = 10 ;
15 = 44 x0,94n ; 0,94n
= 15 /44 ;
n = ln(15/44) / ln(0,94) ~17,4 minutes. [17 ; 18 min].
c. Le programme suivant renvoye la
polus petite valeur de l'entier n pour laquelle Tn > 10. Le compléter.
defseuil()
n=0
T = -19
while T <=10 :
T = -44*0,94^n+25
n = n+1
return n
Exercice A (
Géométrie dans l'espace).
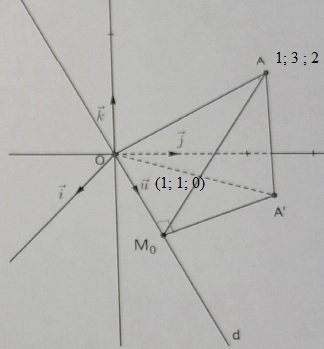
1. Déterminer une représentation paramétrique de la droite d.
x = t ; y = t ; z = 0 avec t réel.
2. Soit t un nombre réel et M un point de la droite d ayant pour cooordonnées (t ; t ; 0).
a. On note AM la distance entre les points A et M. Démontrer que : AM2 = 2t2-8t+14.
Coordonnées de AM ( t-1 ; t-1 ; 0).
AM2 = (t-1)2 +(t-3)2 +22=t2-2t+1 +t2-6t+9 +4=2t2-8t+14.
b. Démontrer que le point M0 de coordonnées (2 ; 2 ; 0) est le point de la droite d pour lequel la distance AM est minimale.
AM est minimale quand AM2 est minimale.
On dérive 2t2-8t+14 et on cherche la valeur de t qui annule cette dérivée : 4t-8 = 0
Soit t = 2.
Si t < 2, 4t-8 est négatif ; si t > 2, 4t-8 est positif.
AM est minimal pour t = 2 et M0(2 ; 2 ; 0).
3. Démontrer que les droite (AM0) et d sont orthogonales.
AM0 est minimal : M0 est le projeté orthogonal de A sur la droite d.
4. On appelle A' (1 ; 3 ; 0) le projeté orthogonal du point A sur le plan d'équation cartésienne z = 0.
Démontrer que M0 est le point du plan (AA'M0) le plus proche du point O.

5. Calculer le volume de la pyramide OM0AA'.
B=Aire de base = aire du triangle rectangle OM0A' = OM0 x A'M0 / 2.
OM0 = (22+22)½ =8½ ;
A'M0 =( (12+12)½ =2½ ;
B =8½ x2½ / 2 = 4 /2 = 2 unités d'aire.
Hauteur de la pyramide AA' = 2.
Volume de la pyramide : B x AA' / 3 = 2 x2 / 3 = 4 /3.
Exercice B ( équation différentielle, fonction exponentielle
On considère l'équation différentielle (E) : y' =y +2xex.
1. Démontrer que u(x) = x2ex est une solution particulière de (E).
Calcul de la dérivée en posant w = x2 et v = ex.
w'(x)=2x ; v'=ex ; w' v+ w v'= u ' = 2xex+ x2ex.
Repport dans (E) :
2xex+ x2ex = x2ex+2xexest vérifié quelque soit x.
u(x) = x2ex est donc une solution particulière de (E).
2. Soit f une fonction définie et dérivable sur R. On note g la fonction définie sur R par :
g(x) = f(x) -u(x).
a. Démontrer que si f est solution de (E) alors g est solution de l'équation différentielle y' = y.
g '(x) = f '(x) -u '(x).
f(x) est solution de (E) : f '(x) = f(x) +2xex.
u ' (x)= 2xex+ x2ex.
g '(x) =f '(x) -u '(x) =f(x)-x2ex = f(x) -u(x) = g(x) .
On admet que la réciproque de cette propriété est vraie.
b. Résoudre (E).
Solution générale de y' = y : g(x).
Solution particulière de (E) : u(x).
Solution générale de (E) : g(x) + u(x).
3. Etude de la fonction u.
a. Etudier le signe de u'(x) sur R.
b. Dresser le tableau de variation de la fonction u sur R ( les limites ne sont pas demandées).
u ' (x)= 2xex+ x2ex = ex(x+2)x.
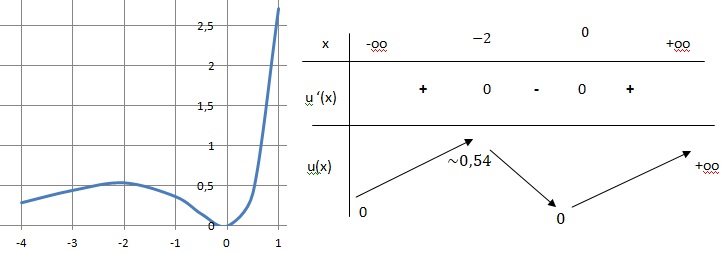
c. Déterminer le plus grand intervalle sur lequel la fonction u est concave.
u'(x) = ex(x2+2x).
Calcul de la dérivée seconde en posant w = ex ; v =x2+2x.
w' = ex ; v' = 2x+2.
w" = ex(x2+2x) +2(x+1)ex =ex( x2+4x+2) .
ex >0, le signe de u"(x) est celui de x2+4x+2.
Racines de x2+4x+2=0
D =42-8 = 8.
x1 = (-4+8½) / 2 ~ -0,59 et x2 =x1 = (-4-8½) / 2 ~ -3,4.
La dérivée seconde étant négative sur ] (-4-8½) / 2 ; (-4+8½) / 2 [, la fonction u est concave sur cet intervalle.
|
|