De
la Terre à la Lune, de Jules Verne à Saturn V, bac STL biotechnologies
2020.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
..
..
|
.
.
|
..
..
......
...
|
A. Le
Trajet Terre-Lune.
A.1. Trajet Terre-Lune dans le roman de Jules
Verne.
J. Verne imagine un projectile piloté par un équipage de trois
personnes et lancé à l'aide d'un canon de hauteur h = 100 m. Il
considère un trajet direct, en ligne droite.
A.1.1. Mesure de la
distance Terre-Lune par une méthode moderne.
Des réflecteurs ont été déposés à la surface de la Lune pour réaliser
des mesures de la distance Terre-Lune au moyen d'un faisceau laser de
longueur d'onde l =
532 nm.
La durée d'un aller retour Dt
est égale à 2,33 s entre l'émission d'une impulsion et la
réception du signal lumineux de retour.
A.1.1.1 Déterminer
la distance dTL Terre-Lune.
dTL = c Dt
/ 2 = 3,00 108 x2,33 / 2 ~3,50 108 m.
A.1.1.2. Citer le
domaine des ondes électromagnétiques auquel appartient ce rayonnement.
Donner l'intervalle de longueur d'onde de ce domaine.
532 nm appartient au domaine visible [ 400 ; 800 nm ].
4.1.2. La distance
Terre-Lune dans le roman de Jules Verne.
A.1.2.1. Indiquer
les positions apogée et périgée sur la trajectoire de la Lune autour de
la Terre.
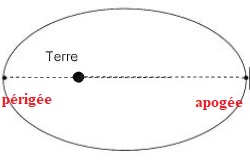
A.1.2.2. Indiquer
en km la valeur de la plus petite distance dTLmin entre la
Terre et la Lune selon Jules Verne.
88 010 lieues ; 1 lieue = 4,0 km.
dTLmin =88 010 x4,0 =3,5 105
km.
A.1.2.3. Dans le
référentiel géocentrique, la durée du trajet Terre-Lune est de 97 h 20
min.
Comparer la vitesse moyenne du projectile imaginé par l'auteur pour
atteindre la Lune à celle des ondes sonores dans l'air. Commenter.
97 h 20 min = 97 x3600 +20 x60 =3,5 105 s.
Vitesse : 3,5 105 / (3,5 105) = 1,0 km /s, valeur
supérieur à 340 m /s.
Le projectile passe le mur du son.
A.1.3.
L'accélération du projectile dans le roman de Jules Verne.
La vitesse de libération v1 du projectile de masse m est la
vitesse minimale que doit avoir le projectile pour s'échapper de
l'attraction terrestre. Jules Verne donne une valeur v1 =
1,20 104 yards / s. ( 1 yard = 0,914 m).
La vitesse du projectile à la sortie du canon est v1 et sa
vitesse initiale v0 est nulle.
A.1.3.1. En
supposant que le projectile assimilé à un point matériel subit un
mouvement uniformément accéléré à l'intérieur du canon, la relation
suivante peut être utilisée :
v12-v02 = 2ah.
Calculer la valeur de l'accélération a du projectile.
v1 = 1,20 104 x0,914 =1,097 104 m /s.
a = v12/(2h)
=(1,097 104)2 /(2x100)=6,0 105 m s-2.
A.1.3.2. Calculer
le nombre de "g" Ng que subissent projectile et occupants.
Conclure.
Ng = a / g = 6,0 105
/9,81 ~6,1 104. ( lésions sévères, mort des occupants).
A2. Le trajet Terre-LUne lors de la mission
Apollo 11.
La première étape consiste en une mise en orbite terrestre et la
seconde étape consiste en un trajet vers la lune avant une mise en
orbite lunaire. Lors du décollage, l'éjection des gaz des réacteurs
développe une force de poussée propulsant la fusée à travers
l'atmosphère.
A.2.1. Le décollage
de Saturn V.
A.2.1.1 Citer les
forces qui s'exercent sur Saturn V au moment du décollage.
Le poids, vertical, vers le bas et la poussée des moteures,
verticale, vers le haut. La vitesse étant faible, les frottements
sont négligeables.
A.2.1.2. Donner la
valeur de ces forces.
Masse m = 2767 t = 2,767 106 kg.; Poids = m g = 2,767 106
x9,81 ~2,71 107 N = 27,1 MN.
Poussée : 33,4 MN
A.2.1.3 Représenter
les forces citées précédemment.
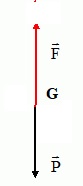
A.2.1.3. Justifier
le décollage de la fusée.
La poussée des moteurs est supérieure au poids : la fusée décolle.
A.2.2.
L'accélération de Saturn V.
Comparer l'accélération du projectile du roman de Jules Verne à
l'accélération maximale ( 38 m s-2) de la fusée Saturn V au
cours de son ascension. Commenter.
6,1 104 /
38 ~1,6 103.
L'accélération
maximale ( 38 m s-2) de la fusée Saturn V est 1600 fois plus
faible que celle du projectile du roman.
38 m s-2 est inférieure à la
limite de résistance humaine ( 46 m s-2).
|
...
|
....
|
B. Les différents modes de propulsion.
Jules Verne propose l'utilisation d'un canon à poudre noire.
B.1. La propulsion solide dans le
roman de Jules Verne.
On donne l'équation de combustion de la poudre noire.
2 KNO3(s) +3C(s) + S(s) --> K2S(s) + 3CO2(g)
+ N2(g).
B.1.1. Citer deux
dangers liés aux combustions.
Incendies et explosions.
B.1.2. Montrer que
la valeur de l'enthalpie molaire standard DcH° de la
réaction de combustion de la poudre noire est -577 kJ mol-1
à 298 K.
DcH° =DfH°(K2S(s))
+3DfH°(CO2(g))
+ DfH°(N2(g))
-2 DfH°(KNO3(s))
-3 DfH°(C(s))- DfH°(S(s)).
DcH° = -381-3
x394 +0-2(-493)3x0-0 = -577 kJ mol-1.
B.1.3. En déduire
l'énergie libérée par une mole de nitrate de potassium au cours de la
réaction de combustion de la poudre noire.
E = -577 kJ mol-1.
B.1.4. Sachant qu'il y a 750 g de
nitrate de potassium dans 1 kg de poudre noire, en déduire l'énergie
libérée par kg de poudre noire lors de cette combustion.
M(KNO3) = 39,1 +14 +3 x16 =71,1 g / mol.
Quantité de matière : 750 / 71,1 =10,55 mol.
E' = -577 x 10,55 ~ -6,1 103 kJ = -6,1 MJ.
B2. La propulsion
chimique liquide de Saturn V.
Le premier étage du lanceur utilise du dioxygène liquide ( LOX) comme
oxydant et du kérosène ( principalement C11H24)
comme réducteur.
Volume du kérozène liquide : 7,45 105 L; masse
volumique 8,00 102 g / L.
Volume du LOX : 1,21 106
L; masse volumique 1,15 103 g / L.
B.2.1. Citer le
mode de production du kérozène.
Distillation fractionnée du pétrole.
B.2.2. Ajuster
l'équation de la réaction de combustion complète du kérosène.
C11H24 (l) + 17O2(g) --> 11 CO2(g)
+ 12H2O(g)
B.2.3. Calculer la quantité de
matière de kérozène.
Masse m = 7,45 105 x 800 =5,96 108 g.
M(C11H24) =11
x12 +24 =156 g/mol.
nkérozène = 5,96 108 / 156 ~3,82 106
mol.
B.2.4 Montrer que
la masse de LOX nécessaire à la combustion complète du kérozène est de
l'ordre de 2 109 g.
n(O2) = 17 nkérozène
=17 x 3,82 106 =6,49 107 mol.
Masse de LOX : n(O2) M(O2)
=6,49 107 x32 =2,1 109 g.
B.2.5. Comparer
cette masse à celle contenue dans le réservoir de LOX.
Masse de LOX : 1,21 106 x 1,15 103 ~1,4 109
g, inférieur à 2 109 g.
Le LOX est en défaut ; le kérozène est en excès.
B.2.6. L'énergie
libérée par la combustion d'un kilogramme de kérozène est de 44 MJ.
Calculer l'énergie Edécollage libérée lors du décollage par
la combustion du kérozène sachant que l'on utilise les 2 / 3 de
la masse embarquée de kérozène.
Masse de kérozène utilisé : 5,96 105 x2 / 3 = 3,97 105
kg.
Edécollage =44 x3,97 105 ~1,75 107 MJ.
B.2.7. En déduire
la masse de poudre noire qui aurait été nécessaire au décollage de
Saturn V.
1,75 107 / 6,1
~2,9 106 kg = 2,9 103 tonnes, soit environ 10
fois plus que la masse de kérozène utilisé.
La poudre noire n'urait pas pu être utilisée pour le décollage de
Saturn V.
C. Jules Verne avait-il
tout imaginé ?
C.1. Des éléments
chimiques sur la Lune.
L'analyse isotopique des échantillons de roches lunaires montre que la
Lune et la Terre sont étrangement similaires. On a mis en évidence un
isotope radioactif du potassium, le potassium 4019
K.
C.1.1. Définir la
notion d'isotopes.
Des isotopes ne se différencient que par leur nombre de neutrons. Ils
ont le même numéro atomique Z.
C.1.2. Le potassium
40 peut se désintégrer en calcium 40.
4019 K
---> 4020
Ca + 0-1 e.
C.1.2.1 Donner la
nature de la particule émise.
Electron 0-1
e.
C.1.2.2. Déterminer
le type de radioactivité correspondant à cette désintégration.
Radioactivité ß-.
C.1.3. Le radon est
un gaz radioactif. Il se désintègre en polonium 218 en émettant une
particule alpha. Donner le nom et le symbole de cette particule a.
Noyau d'hélium 42He.
C.1.4. Un
échantillon de roches lunaires analysées contenant 1,67 µg de potasium
40. L'activité de 1 g de potassium 40 est A1 = 265,3 kBq.
C.1.4.1 Donner la
définition de l'activité d'une source radioactive.
L'activité correspond au nombre de désintégration par seconde.
C.1.4.2. Calculer
l'activité de cette roche si elle est due uniquement au potassium 40.
A =265,3 103 x1,67 10-6 =0,443 Bq.
. Sachant que
l'échantillon de roche lunaire s'élève à 1 g, conclure quant à la
dangerosité de l'échantillon ramené vis à vis de sa radioactivité vu
qu'un échantillon de 1 kg de granite terrestre a une activité de
l'ordre de 1000 Bq.
L'activité de l'échantillon est deux fois plus
faible que celle du granit terrestre.
C.2. De l'eau sur la Lune.
De l'eau se trouve aux pôles nord et sud de la Lune, dans des cratères
où les rayons du soleil ne pénètrent pas et où la température peut
atteindre -238 °C. Patm lunaire = 3 10-10 Pa.
C.3.1. Donner
l'état de l'eau dans les cratères du pôle nord.
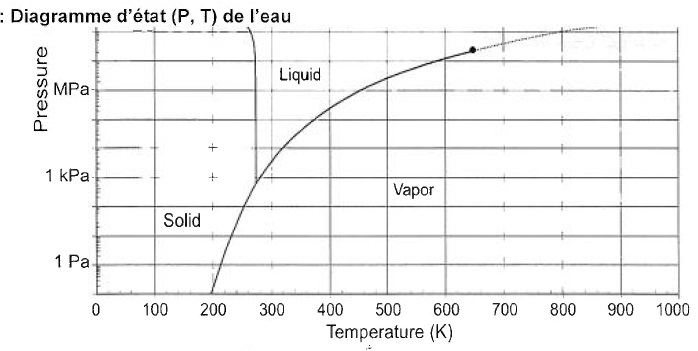
-238°C = 273 -238 =35 K.
L'eau se trouve à l'état solide.
C.2.2. Expliquer
pourquoi l'eau ne peut pas être à l'état liquide sur la Lune
contrairement à qu'avait imaginé Jules Verne.
Sous une pression atmosphérique de 3 10-10 Pa et à 40 K,
l'eau se trouve sous forme solide.
|
|


