Un nanosatellite, bac S Centres étrangers 2020. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. .. .. . . .. .. ...... ... Les satellites X-CubeSat et Spacecube ont été mis au point par des étudiants de l’école polytechnique, de l’école des mines de Paris et du BTS du lycée Diderot à Paris. Ils ont été mis en orbite les 17 et 18 mai 2017 depuis la station spatiale internationale et ont pour mission d'analyser le taux d’oxygène atomique de la thermosphère, partie supérieure de l‘atmosphère. D’après : https://janus.cnes.fr/fr Données : - masse de la Terre : MT = 5,97 × 1024 kg - rayon de la Terre : RT = 6 400 km - constante universelle de gravitation : G = 6,67 × 10-11 S.I. - vitesse de la lumière dans le vide : c = 3,00 × 108 m.s-1. On se place dans le référentiel géocentrique. 1. Orbite de Spacecube. Les caractéristiques de l’orbite de Spacecube sont les suivantes : - altitude minimale au point P : 395 km - altitude maximale au point A : 402 km - nombre de révolutions par jour : 15,56 1.1. Montrer par un calcul d’écart relatif qu’il est possible de considérer que l’orbite de ce satellite est quasi-circulaire. 6400+402=6802 km ; 6400+395=6795 km.  Ecart : 7 km. ; écart relatif : 7 / 6800 =1,0 10-3 ( 0,1 %).. L’orbite de ce satellite est quasi-circulaire. On considère dans la suite de l’exercice l’orbite circulaire, d’altitude h = 400 km. 1.2. Exprimer la vitesse v du satellite en fonction de sa période de rotation T et du rayon de l’orbite R. Le satellite parcourt la circonférence p(RT+h) en T seconde à la vitesse v. 2p(RT+h) = vT ; v = 2p(RT+h) / T = 2p R / T. 1.3. Donner l’expression de l’accélération aN du satellite dans le cas d’un mouvement circulaire. aN = v2 / R =4p2 R / T2. 1.4. À l’aide de la seconde loi de Newton et des réponses aux questions précédentes, calculer le nombre de révolutions effectuées par jour par ce satellite. Conclure quant à l’approximation d’une orbite circulaire. L'accélération centripète s'exprime par : MT G / R2. MT G / R2 =4p2 R / T2. T2 = 4p2 R3 /( MT G) =4x3,142 x(6,8 106)3 / (6,67 10-11 x5,97 1024) ~3,117 107 s2 ; T ~5,58 103 s. Nombre de révolutions efféctuées chaque jour : 24 x3600 / (5,58 103) ~15,47. Ecart relatif : (15,56 -15,47) / 15,56 ~5,8 10-3 ( 0,6 %). L’approximation d’une orbite circulaire est correcte. ... .... 2. Transmission des données recueillies Les mesures donnant accès au taux d’oxygène atomique de la thermosphère sont effectuées par spectroscopie dans l’U.V. lointain (l < 200 nm) et transmises sur Terre avec une onde radio de fréquence 436 MHz. Il est également possible d’envoyer des commandes au satellite grâce à une onde radio à 146 MHz. 2.1. Expliquer pourquoi il est nécessaire que les mesures du taux d’oxygène atomique de la thermosphère soient réalisées depuis un satellite. Limite inférieure de la thermosphère 95 km ; limite supérieure comprise entre 500 et 1000 km. Dans la thermosphère, les molécules de dioxygène se dissocient en deux atomes d'oxygène sous l'action des UV solaires de très courtes longueurs d'onde ( entre 100 et 200 nm). Ces derniers sont bloqués en haute atmosphère. 2.2. Justifier le choix des fréquences utilisées pour communiquer avec le satellite depuis la Terre. 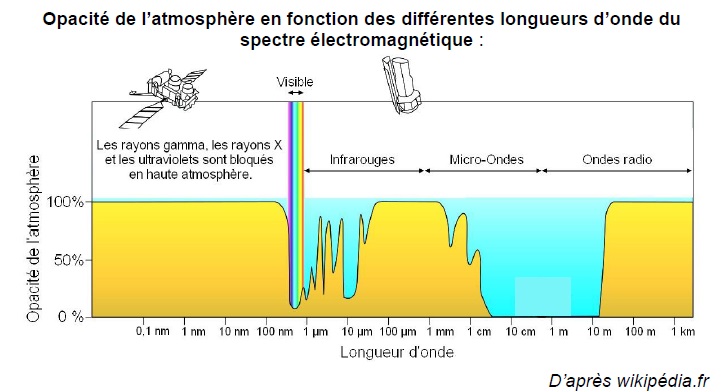Longueur d'onde correspondant à 436 106 Hz : 3,00 108 / (436 106) ~0,69 m. L'atmosphère n'absorbe pas ces ondes. Longueur d'onde correspondant à 146 106 Hz : 3,00 108 / (146 106) ~2,1 m. L'atmosphère n'absorbe pas ces ondes. .

menu