Détermination
de la masse de la Lune, bac Centres étrangers 2021.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
..
..
|
.
.
|
..
..
......
...
|
Galilée a établi que la vitesse d'un objet en chute libre est indépendante de sa mmasse.
Une vérification expérimentale a été réalisé sur la lune en 1971 : un
marteau et une plume lâchés simultanément d'une même hauteur, sans
vitesse initiale, touchent le sol au même instant.
Cette expérience permet également d'estimer la masse de la lune.
le mouvement du cenntre de masse du marteau est étudié dans un
référentiel lumaire supposé galiléen. L'origine est choisie au niveau
du sol. Le pointage des positions du marteau débute à un instant choisi
comme origine des dates lorsqu'il se trouve à 1,43 m du sol. Sa vitesse
v0 est verticale, dirigée vers le bas. La chute est verticale suivant l'axe Oy orienté vers le haut.
Le tableur utilisé permet de modéliser la courbe y = f(t) représenntant
l'évolution temporelle des positions par une parabole d'équation
y=-0,865 t2 -0,15 t +1,43.
Questions préliminaires.
1. Compte tenu de
la faible hauteur initiale, on considère que la distance entre le
centre de la lune et le marteau tout au long de sa chute est égale au
rayon lunaire R.
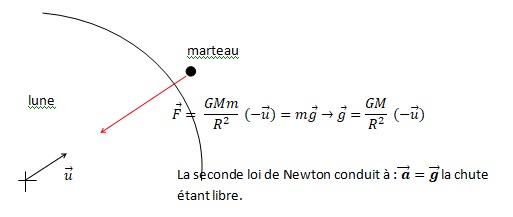
Donner l'expression vectorielle de la force gravitationnelle modélisant
l'action exercée par la lune sur le marteau en fonction de la masse de
la lune M, de la masse du marteau m, du rayon lunaire R et d'un vecteur
unitaire orienté du centre de la lune vers la surface lunaire. Faire un
schéma.
2. Donner l'expression du champ de pesanteur lunaire.
3. Donner l'expression du vecteur accélération du marteau.
Problème.
Déterminer la masse de la lune.
G = 6,67 10-11 N m2 kg-2 ; R = 1,74 106 m.
y= -0,865 t2 -0,15 t +1,43 conduit à : ½g = 0,865 soit g = 1,73 m s-2.
g = GM / R2 ; M = gR2 / G = 1,73 x(1,74 106)2 / (6,67 10-11)=7,85 1022 kg.
Ecart relatif avec la valeur de référence 7,34 1022 kg.
(7,85-7,34) / 7,85 ~0,07 ( 7 %).
Une explication possible sur cet écart : imprécision sur la valeur -0,865 m s-2.
|