Les
supercondensateurs, bac Centres étrangers 2021.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
..
..
|
.
.
|
..
..
......
...
|
1.
Comparer la valeur de la capacité du supercondensateur étudié aux
valeurs usuelles des capacités des condensateurs utilisés au lycée ou
en électronique.
Capacité d'un supercondensateur : 400 F.
Capacité d'un condensateur utilisé en électronique : très inférieure à 1 F.
La valeur de la capacité d'un condensateur plan est : C = e S / d.
S : surface des armatures en regard ; d : distance des armatures ; caractériqtique de l'isolant placé entre les armatures.
2. Justifier qualitativement le texte suivant.
Si des condensateurs classiques étaient utilisés à la place des
supercondensateurs, il faudrait des armatures de très grande surface et
très rapprochées, séparées par un excellent diélectrique.
La capacité d'un condensateur est proportionnelle à la surface des
armatures et inversement proportionnelle à la distance qui les sépare.
Etude du modèle du circuit RC série.
On considère le circuit électrique schématisé ci-dessous composé d'une
source idéale de tension E, d'in interrupteur K, d'un conducteur
ohmique de résistance R, du supercondensateur de capacité C et d'un
ampèremètre de résistance interne négligeable. ( la tension aux bornes
de l'ampèremètre est considérée comme nulle).
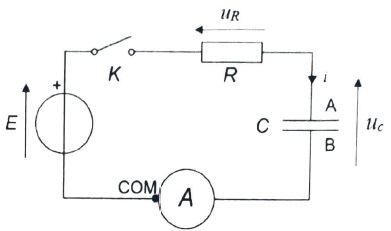
Le supercondensateur esst initialement déchargé. A l'instant t=0, on ferme l'interrupteur.
3. Donner la
relation entre l'intensité i(t) et la dérivée de la charge q(t)
portée par l'armature A, puis la relation entre i(t), la capacité et la
dérivée de la tension uC(t) aux bornes du supercondensateur.
i(t) = dq(t) / dt.
q = Cuc(t) ; i(t) = Cduc(t) / dt.
4. Montrer que l'équation différentielle régissant la tension uc(t) est de la forme :
duc(t) / dt + 1 /t uc(t) = E / t.
Exprimer t en fonction de R et C.
Additivité des tensions :E = Ri(t) + uc(t).
E = RCduc(t) / dt +uc(t).
On pose t = RC.
duc(t) / dt + 1 /t uc(t) = E / t.
5. duc(t) / dt + 1 /t uc(t) = E / t.vérifier que les solutions de cette équation sont de la forme :
uc(t) = A e-t / t +E.
Donner l'expression de A.
On dérive : duc(t) / dt =-A / t e-t / t ; repport dans l'équation différentielle :
-A / t e-t / t +A / t e-t / t +E = E est vérifiée quel que soit t.
A t=0, uc(0) = 0 : 0 = A+E ; A = -E.
|
...
|
....
|
Etude expérimentale et détermination de la valeur de la capacité.
On utilise le montage précédent avec E = 2,5 V et R = 2,0 ohms.
On réalise le suivi temporel de la tension aux bornes du condensateur durant sa charge.
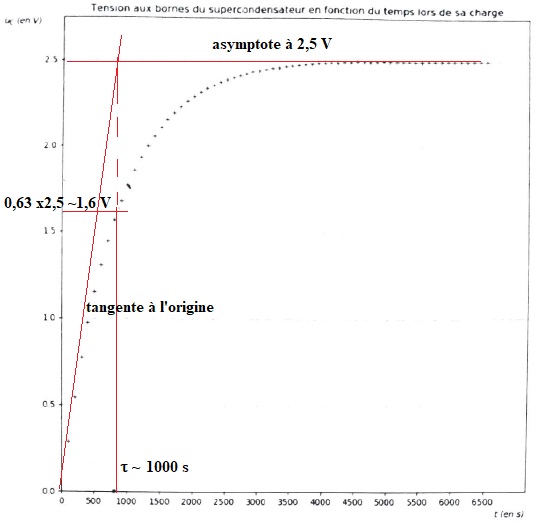
6. Déterminer la capacité C1 du supercondensateur.
RC1 = 1000 ; C1 = 1000 / R = 1000 / 2,0 = 5,0 102 F.
Après 10 exécutions d'un programme python, on obtient pour le temps caractéristique t, la série de valeurs suivantes exprimées en ms.
811614 ; 818076 ; 810301 ; 818526 ; 812067 ; 811327 : 813109 ; 817838 ; 819474.
Moyenne de la série : 814,2827 s ; incertitude-type 1,175 s.
7. Ecrire de manière appropriée le résultat de la mesure du temps caractéristique et de son incertitude.
t =( 814 ±1) s.
On estime u(R) = 0,1 ohm
u(C) = C ( (uR / R)2 +(u(t) / t)2 )½.
8. Déterminer C ainsi que son incertitude.
C = t / R = 814 / 2,0 =407 ~4,1 102 F.
u(C) = 407 ( (0,1 / 2)2 +(1,175 / 814,28)2 )½.
u(C) = 407 (2,5 10-3 +2,08 10-6)½ ~20 F.
C = 4,1 102 ± 20 F.
9. Comparer cette valeur avec celle donnée par le constructeur ( 400 F) et conclure.
Ecart relatif : (410-400 ) / 400 ~0,025 ( 2,5 %).
A 2,5 % près ces deux valeurs sont en accord.
|
|