Mathématiques,
fonctions, suite, géométrie, bac Centres étrangers 2021.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
...
|
.
.
|
..
..
......
...
|
Exercice 1, QCM ( 5 points).
Question 1.
Soit la fonction g définie sur ] 0 ; +oo[ par : g(x) = x2+2x-3 / x.
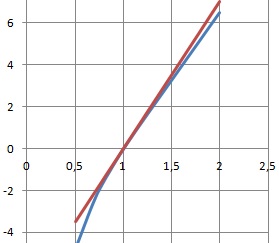
Une équation de la tangente à la courbe représentative de g au point d'abscisse 1 est :
y = 7(x-1) vrai.; y = x-1 ; y =7x+7 ; y = x+1.
Dérivée g'(x) = 2x+2+3/x2.
Coefficient directeur de la tangente : g'(1) =7.
Le point de coordonnée (1 ; g(1) =0 appartient à la tangente.
Equation cherchée : y = 7x+b ;
0 = 7 +b ; b = -7.
Question 2.
On considère la suite (vn) par vn = 3n /(n+2). La limite de cette suite en plus l'infini est :
1 ; 3 vrai ; 1,5 ; on ne peut pas la déterminer.
Mettre n en facteur commun au dénominateur et au numérateur.
3n / (n(1+2 / n).
Simplifier par n : 3 /(1+2 / n).
2 / n tend vers zéro quand n tend vers plus l'infini et vn tend vers 3.
Question 3.
Une urne contient 6 boules noires et 4 boules rouges. On effectue
successivement 10 tirages aléatoires avec remise. Quelle est la
probabilité d'avoir 4 boules noires et 6 boules rouges ?
0,1662 : 0,4 ; 0,1115 vrai ; 0,8886.
Soit l'événement " on tire une boule rouge", de probabilité 0,4.
Soit X la variable aléatoire associée au nombre de boules rouges tirées.
X suit la loi binomiale de paramètres n = 10 ; p = 0,4.
P(X = 6) = 0,1115.
Question 4. On considère la fonction f définie sur R par f(x) = 3ex-x.
La limite de f en plus l'infini est :
3 ; +oo vrai ; -oo ; on ne peut pas déterminer cette limite.
f(x) = ex(1-x / ex).
Par croissance comparée, x / ex tend vers zéro si x tend vers plus l'infini.
Question 5.
Un code inconnu est constitué de 8 signes. Chaque signe peut être une
lettre ou un chifftre. Il y a donc 36 signes utilisables pour chacune
des positions. Un logiciel de cassage de code teste environ cent
millions de codes par seconde.
En combien de temps maximum ce logiciel peut-il découvrir ce code ?
0,3 s ; 8 heures vrai ; environ 3 heures ; environ 470 heures.
368 / 108 =2,8 104 s soit environ 8 heures.
Exercice 2. 5 points.
Au premier janvier 2020, la centrale solaire Big Sun possédait 10560
pannneaux solaires. On observe chaque année, que 2 % des panneaux se
sont détériorés et nécessitent d'être retirés tandis que 250 nouveaux
panneaux solaires sont installés.
On modélise l'évolution du nombre de panneaux solaires par la suite (un) définie par u0 = 10560 et un+1 =0,98 un +250.
1.a. Expliquer en quoi cette modélisation correspond à la situation étudiée.
Chaque année, 2 % des panneaux sont retirés: sur 100 panneaux, il en reste 98.
On installe de plus 250 nouveaux panneaux par an.
b. On souhaite
savoir au bout de combien d'années le nombre de panneaux solaires sera
strictement supérieur à 12 000. Donner la réponse à ce problème à
l'aide de la calulatrice.
La calculatrice donne n = 68. ( 1er janvier 2088 ).
c. Recopier et
compléter le programme en Python ci-dessous de sorte que la
valeur cherchée à la question précédente soit stockée dans la
variable n à l'issue de l'exécution de ce dernier.
u = 10560
n=0
while u < 12000 :
u = u*0,98 +250
n = n+1.
2. Démontrer par récurrence que un < 12500.
Initialisation : u0 = 10560 ; la propriété est vraie au rang zéro.
Hérédité : la propriété est supposée vraie au rang n : un < 12500.
un+1 = 0,98 un +250.
un+1 < 0,98 *12500 +250 ; un+1 < 12500.
La propriété est vraie au rang n+1.
Conclusion : la propriété est vraie au rang zéro et héréditaire, elle est donc vraie pour tout n.
3. Démontrer que cette suite est croissante.
un+1 -un=0,98 un +250 -un =250 -0,02 un.
un < 12500 ; 0,02 un < 12500 x0,02 ; un < 250
250 -0,02 un > 0.
un+1 -un>0 , la suite est croissante.
4. En déduire que cette suite converge, sans calculer sa limite.
La suite est croissante et majorée, donc elle converge.
5. On définit la suite (vn) par vn = un -12500.
a. Démontrer que (vn) est géométrique de raison 0,98 dont on déterminera le premier terme.
vn+1 = un+1 -12500.
un+1 =0,98 un +250.
vn+1 = 0,98 un-12500 +250 = 0,98 un -12250.
vn+1 =0,98 (un-12500) =0,98 vn.
v0 = u0-12500 =10 560-12 500= -1940.
b. Exprimer vn en fonction de n.
vn = -1940 x 0,98n.
c. En déduire un en fonction de n.
un = vn +12500 =12500-1940 x0,98n.
d. Déterminer la limite de la suite (un) et interpréter.
-1 < 0,98 < 1, donc 0,98n tend vers zéro quand n tend vers plus l'infini.
La suite (un) tend vers 12500.
Au bout d'un temps suffisamment long, le nombre de panneaux sera égal à 12500.
Modélisation à l'aide d'une fonction.
Le nombre de panneaux solaires peut être estimé par la fonction f définie sur [0 ; +oo[ par f(x) = 12500-500e-0,02x+1,4 où x représente le nombre d'années écoulées depuis le 1er janvier 2020.
1. Etudier le sens de variation de cette fonction.
f '(x) = -500 x(-0,02) e-0,02x+1,4 = 10e-0,02x+1,4 .
f '(x) est strictement positive ; la fonction f(x) est strictement croissante.
2. Déterminer la limite de la fonction f en plus l'infini.
Le terme en exponentielle tend vers zéro et f(x) tend vers 12500.
3. Avec ce modèle, au bout de combien d'années le nombre de panneaux solaires dépassera 12000.
12500-500e-0,02x+1,4 =12 000.
500 = 500e-0,02x+1,4 ; 1 = e-0,02x+1,4 ; ln(1 ) =-0,02x+1,4.
0 = -0,02x+1,4 : x = 1,4 / 0,02 =70.
|
...
|
....
|
Exercice 3. (5 points)
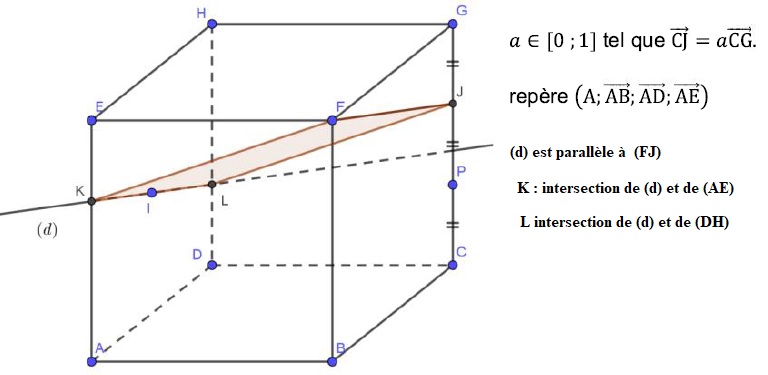
Partie A. Dans cette partie a = 2 /3.
1. Donner les coordonnées des points F, I et J.
F(1 ; 0 ; 1) ;
I est le centre de la face ADHE : I(0 ; 0,5 : 0,5).
J( 1 ; 1 ; a) soit (1 ; 1 ; 2/3)
2. Déterminer une représentation paramétrique de la droite (d).
Coordonnées du vecteur FJ : ( 0 ; 1 ; a-1) soit (0 ; 1 ; -1/3).
Représentation paramétrique de la droite (d) :
x = xI =0 : y = t+yI = t+ 0,5 : z = -t/3+zI = -t/3+0,5 avec t réel.
3.a Montrer que les coordonnées du point K sont (0 ; 0 ; 2/3).
K appartient à (AE); K( 0 ; 0 ; zK).
K appartient à (d) : xK=0 ; yK=0=t+0,5 soit t = -0,5 : zK = 1/ 6 +1 /2 = 4 /6 = 2 /3.
b. Déterminer les coordonnées du point L.
Coordonnées du vecteur DH : ( 0 ; 0 ; 1).
Représentation paramétrique de la droite (DH) :
x = xD =0 : y = yD = 1 ; z = t'+zD = t' avec t réel.
L appartient à DH : xL =0 ; yL = 1 ; zL = t'.
L appartient à (d) : 1=t+0,5 soit t = 0,5 ; zL = -1/6+1/2=1/3.
L( 0 ; 1 ; 1/3).
4.a Démontrer que le quadrilatère FJLK est un parallélogramme.
FJ =(12 +(-1/3)2)½ =(10/9)½ = 10½ / 3.
KL =(12 +(-1/3)2)½ =(10/9)½ = 10½ / 3.
KF =(12 +(1/3)2)½ =(10/9)½ = 10½ / 3.
LJ =(12 +(-1/3)2)½ =(10/9)½ = 10½ / 3.
Les côtés opposés ayant même mesure, le quadrilatère FJLK est un parallélogramme.
b. Démontrer que le quadrilatère FJLK est un losange.
Les 4 côtés ayant même mesure, le quadrilatère FJLK est un losange.
c. Le quadrilatère FJLK est-il un carré ?
Coordonnées du vecteur KL : ( 0 ; 1 ; -1/3).
Coordonnées du vecteur LJ : ( 1 ; 0 ; 1/3).
Le produit scalaire de ces deux vecteurs n'étant pas nul, le quadrilatère FJLK n'est pas un carré.
Partie B. Cas général.
On admet :K(0 ; 0 ; 1-0,5a) ; L(0 ; 1 ; 0,5a).
1. Déterminer les coordonnées de J en fonction de a.
J(1 ; 1 ; a). F(1 ; 0 ; 1) ;
2. Démontrer que le quadrilatère FJLK est un parallélogramme.
FJ =(12 +(a-1)2)½ =(a2-2a+2)½ .
KL =(12 +(1-a)2)½ =(a2-2a+2).
KF =(12 +(0,5a)2)½ =(1+0,25a2)½ .
LJ =(12 +(0,5a)2)½ =(1+0,25a2)½ .
Les côtés opposés ayant même mesure, le quadrilatère FJLK est un parallélogramme.
3. Existe-t-il des valeurs de a telles que le quadrilatère FJLK soit un losange ? Justifier.
Deux côtés consécutifs de ce parallèlogramme doivent avoir même mesure.
a2-2a+2 = 1+0,25a2.
0,75 a2-2a+1 = 0.
Discriminant D =(-2)2 -4*0,75 = 1
Solutions : a =(2-1)/ 1,5 = 2 /3.
a = (2+1) / 1,5 =2, impossible a est compris entre 0 et 1.
4. Existe-t-il des valeurs de a telles que le quadrilatère FJLK soit un carré ? Justifier.
D'après la question 4. c de la partie A, la réponse est non.
|
|