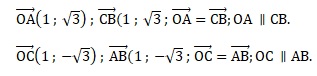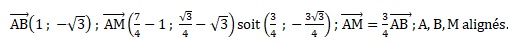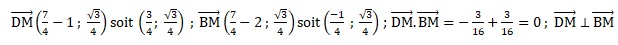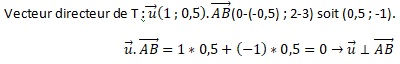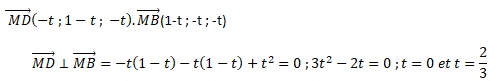Mathématiques,
bac S Nlle Calédonie 02/12 /2020.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
..
..
|
|
......
.....
|
Exercice 1.
( 5 points ).
1.On considère l'équation (E) z3=4z2-8z+8 ayant pour inconnue le nombre complexe z.
a. Démontrer que, pour tout nombre complexe z :
z3-4z2+8z-8=(z-2)(z2-2z+4).
(z-2)(z2-2z+4)= z3-2z2+4z-2z2+4z-8 = z3-4z2+8z-8.
b. Résoudre (E).
z-2=0 soit z = 2.
z2-2z+4=0 ; discriminant D =(-2)2-4*4 = -12 = 12 i2 =(2i 3½)2.
z1=(2 +2i 3½) / 2 =1+i 3½.
z2=(2 -2i 3½) / 2 =1-i 3½.
c. Ecrire les solutions de (E) sous forme exponentielle.
z = 2 exp(i 2p).
Module de z1 ou de z2 : |z1|= (12+3)½ = 2
z1 / |z1| =0,5 +i 3½ / 2 = cos (p/3 )+ i sin (p /3 ) ; z1 = 2 exp(i p/3).
z2 / |z2| =0,5 -i 3½ / 2 = cos (-p/3) + i sin (-p /3 ) ; z2 = 2 exp(-i p/3).
On muni le plan complexe d'un repère orthonormé direct. Soit A, B, C et D les points d'affixes respectives :
zA = 1+i 3½ ; zB = 2 ; zC = 1-i 3½ ; zD=1.
Ces quatre points sont reprsentés dans la figure ci-dessous.
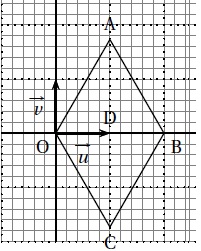
2. Quelle est la nature du quadrilatère OABC ? Justifier.
A(1 ; 3½) ; B(2 ; 0) ; C(1 ; -3½).
OA =(1+3)½ = 2 ; OC=(1+3)½ = 2 ; AB=( 1+(3½)2)½ = 2 ; BC=( 1+(-3½)2)½ = 2.
Les quatre côtés du quadrilatère OABC sont égaux.
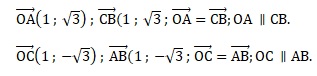
Le quadrilatère OABC est un losange.
3. Soit M le point d'affixe zM = 7 / 4 +i 3½ / 4.
a. Démontrer que les points A, M et B sont alignés.
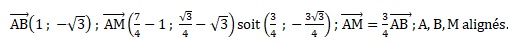
b. Démontrer que le triangle DMB est rectangle.
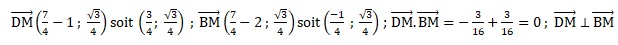
Exercice 2. 5 points.
Le phaéton est un oiseau des régions intertropicales
1. Lorsque le
phaéton à bec rouge vit dans un environnement pollué, sa durée de vie
en années, est modélisée par une variable aléatoire X suivant une loi
normale d'espérance µ inconnue et d'écart type s = 0,95.
a. On considère la variable aléatoire Y = (X-µ) / 0,95.
Donner sans justification la loi suivie par Y.
Y suit la loi normale centrée réduite N(0 ; 1).
b. On sait que P(X > 4) =0,146.
Démontrer que µ=3.
P(X-µ > 4 -µ) = 0,146 ; P((X-µ) / 0,95 > (4 -µ) / 0,95) = 0,146.
P(Y > (4 -µ) / 0,95) = 0,146.
1- P(Y < (4 -µ) / 0,95) = 1-0,146 = 0,854.
La calculatrice donne (4 -µ) / 0,95 =1,053 ; 4-µ =1 ; µ = 3.
2. Lorsque le
phaéton à bec rouge vit dans un environnement sain, sa durée de vie, en
année, est modélisée par une variable aléatoire Z. Les courbes des
fonctions de densité associées aux lois de X et de Z sont représentées.
a. Quelle est la courbe de la fonction de densité associée à X ? Justifier.
X suit la loi normale d'espérance µ = 3 : courbe en forme de chloche
symétrique par rapport à la droite verticale d'équation µ=3.
b. Hachurer la zone du plan correspondant à P(Z > 4).
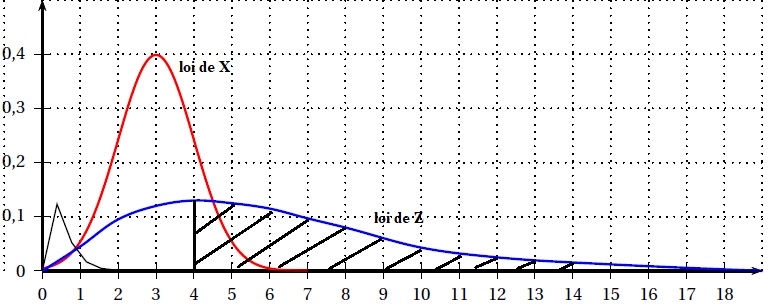
On admettra par la suite que P(Z > 4) = 0,677.
3. Une étude
statistique portant sur une région donnée, a permis d'établir que 30 %
des phaétons à bec rouge vivent dans un environnement pollué ; les
autres vivent dan un environnement sain.
On choisit au hasard un phaéton à bec rouge vivant dans la région donnée. On considère les événements suivants :
S : le phaéton à bec rouge choisi vit dans un environnement sain.
V : le phaéton à bec rouge choisi a une durée de vie d'au moins 4 ans.
a. Compléter l'arbre pondéré suivant.
b. Déterminer P(V).
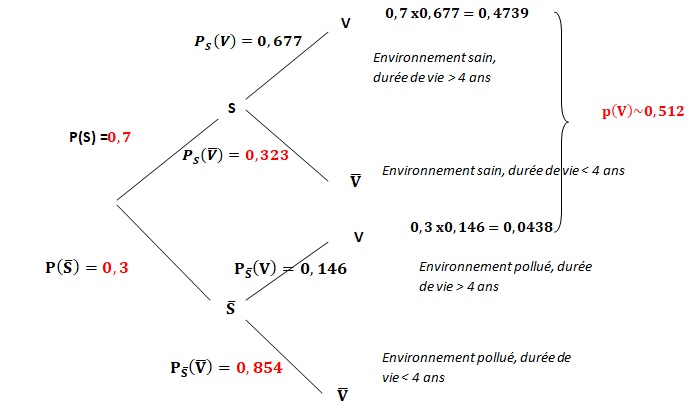
c. Sachant que le
phaéton à bec rouge a une durée de vie d'au moins 4 ans, quelle est la
probabilité qu'il vive dans un environnement sain ?
PV(S) =P(S n V) / P(V) = 0,4739 / 0,512 ~0,926.
|
...
|
|
|
....
|
Exercice 3. ( 5
points).
Partie
A.
Soit g la fonction définie sur l'ensemble des nombres réels par : g(x) =x2+x+0,25+4 /(1+ex)2.
On admet que la fonction g est dérivable et on note g' sa dérivée.
1. Déterminer les limites de g en +oo et -oo.
En plus l'infini : 4 /(1+ex)2 tend vers zéro et g(x) tend vers plus l'infini.
En moins l'infini : ex tend vers zéro ; 4 /(1+ex)2 tend vers 4 et g(x) tend vers plus l'infini.
2. On admet que la fonction g' est strictement croissante sur R et que g'(0)=0.
Déterminer le signe de g'(x) sur R.
Sur ]-oo ; 0 ] ; g'(x) est négative ; sur [ 0 ; +oo ] ; g'(x) est positive.
3. Dresser le tableau de variations de la fonction g et calculer le minimum de la fonction g sur R.
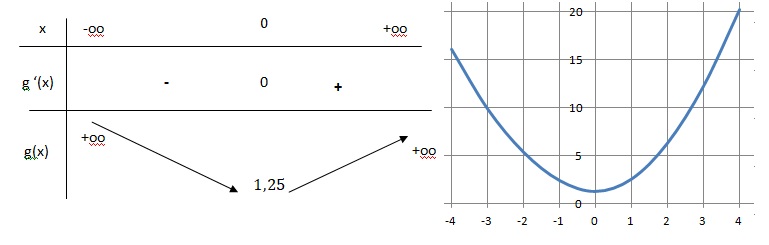
Partie
B.
Soit f la fonction définie sur R par f(x) = 3-2 /(1+ex). On déssigne par C sa courbe représentative représentée ci-dessous.
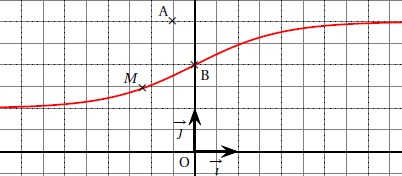
Soit A le point de coordonnées (-0,5 ; 3).
1. Démontrer que le point B (0 ; 2) appartient à C..
f(0) =3-2 / (1+e0) = 3-2 /(1+1) = 2 = yB.
2. Soit x un réel quelconque. On note M le point de la courbe C de coordonnées (x ; f(x)). Démontrer que AM2 = g(x).
AM2 =(xM-xA)2+(yM-yA)2=(x+0,5)2+(f(x)-3)2=x2+x+0,25+f(x)2+9-6f(x).
f(x)2 =9+4 /(1+ex)2-12/(1+ex).
AM2 =x2+x+0,25+9+4 /(1+ex)2-12/(1+ex) +9 -18+12 /(1+ex).
AM2 =x2+x+0,25+4 /(1+ex)2 = g(x).
3. On admet que la distance AM est minimale si et seulement si AM2 est minimal.
Déterminer les coordonnées du point de la courbe C tel que la distance AM est minimale.
AM2 est minimale pour g'(x) = 0 soit x = 0.
f(0) =2 ; M(x ; 2).
4.
On admet que la fonction f est dérivable sur R et on note f ' sa fonction dérivée.
a. Calculer f '(x).
On pose u = 1+ex ; u' = ex ; -u'/u2 =ex/(1+ex)2 ; f '(x) = 2ex/(1+ex)2 .
b. Soit T la tangente à la courbe C au point B. Démontrer que l'équation réduite de T est y = 0,5x+2.
Coefficient directeur de T : f '(0) =2 /(1+1)2 = 0,5.
y = 0,5 x+b ; B(0 ; 2) appartient à T d'où 2=b.
5. Démontrer que la droite T est perpendiculaire à la droite (AB).
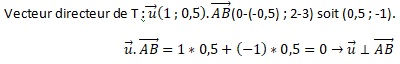
|
Exercice 4. ( 5 points)
Pour chacune des affirmations suivantes, indiquer si elle est vraie ou fausse en justifiant.
Affirmation 1. L'équation (3ln(x)-5)(ex+4)=0 admet exactement deux solutions réelles. Faux.
ex+4=0 n'a pas de solution réelle, ex étant toujours positif.
3ln(x)-5=0 ; ln(x) = 5 /3 ; x = e5/3.
2. On considère la suite (un) définie par u0=2 et un+1=2un-5n+6.
Affirmation 2. Pour tout entier naturel n, un = 3*2n+5n-1. Vrai.
Initialisation : u1 =2u0-5*0+6=4+6=10 ; 3*2n+5n-1=3*2+5-1=10.
La propriété est vraie au rang 1.
Hérédité : la propriété est supposée vraie au rang n. un = 3*2n+5n-1.
un+1=2(3*2n+5n-1)-5n+6=3*2n+1+10n-2-5n+6=3*2n+1+5n+4 = 3*2n+1+5(n+1)-1.
La propriété est vraie au rang n+1.
Conclusion : la propriété est vraie au rang 1 et héréditaire, elle est donc vrai pour tout n entier naturel.
3. On considère la suite (un) définie par un = n2+½. Faux.
Affirmation 3. La suite est géométrique.
un+1 = (n+1)2+½ =n2+2n+1+½ =n2+2n+1,5.
un+1 / un =(n2+2n+1,5) / (n2+½ ) diffère d'une constante.
4. Dans un repère de l'espace, soit d la droite passant par le point A(-3 ; 7 ; -12) et de vecteur directeur 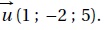
Soit d' la droite ayant pour représentation paramétrique x=2t-1 ; y = -4t+3 ; z = 10t-2, avec t réel.
Affirmation 4. les droites d et d' sont confondues. Vrai.
Coordonnées d'un vecteur directeur de la droite d' ( 2 ; -4 ; 10) soit 2*(1 ; -2 ; 5).
Les deux droites sont parallèles.
Dans l'hypothèse où A appartient à d' ?
xA=2t-1= -3 soit t = -1.
y = -4*(-1)+3 =7 = yA.
z = 10*(-1)-2 = -12 = zA.
L'hypothèse est vraie.
5. On considère un cube ABCDEFGH. L'espace est muni d'un repère orthonormé.
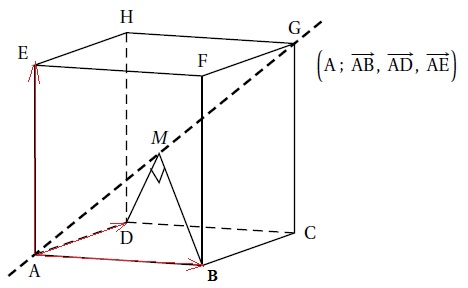
Une représentation paramétrique de la droite (AG) est x=t ; y = t ; z=t avec t réel.
On considère un point M de la droite (AG).
Affirmation 5. Il y a exactement deux positions du point M sur la droite (AG) telles que les droites (MB) et (MD) soient orthogonales. Vrai.
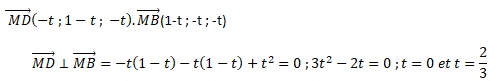
|
|
|