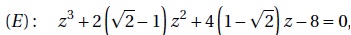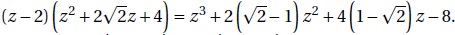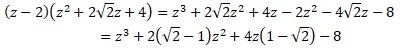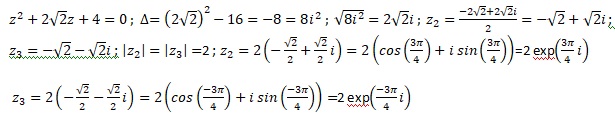Mathématiques,
bac S Nlle Calédonie 02 /2020.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
..
..
|
|
......
.....
|
Exercice 1. ( 6 points ). Partie A.
On considère la fonction f définie sur l’intervalle [0 ; +∞[ par
f (x) = (ax +b)e-0,5x.
où a et b désignent deux nombres réels. On admet que cette fonction est
dérivable sur l’intervalle [0 ; +∞[ et on note f ′ sa fonction dérivée.
Sa courbe représentative Cf est tracée ci-dessous.
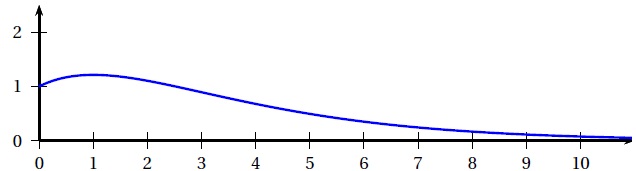
Elle coupe l’axe des ordonnées au point d’ordonnée 1 et admet une tangente horizontale au point d’abscisse 1.
1. Donner les valeurs de f (0) et f ′(1).
f(0) = b=1 ; f ' (1) = 0, tangente horizontale.
2. Démontrer que, pour tout réel positif x, f ′(x) =(-0,5ax-0,5b+a)e-0,5x.
On pose u = ax+b et v = e-0,5x.
u' = a ; v' = -0,5e-0,5x.
u'v +v'u = a e-0,5x-0,5(ax+b)e-0,5x=(-0,5ax-0,5b+a)e-0,5x.
3. Déterminer les valeurs de a et b.
f(0) = b=1 ; f '(1) =0 =(-0,5a-0,5b+a)e-0,5.
0 =(0,5a-0,5)e-0,5 ; a =1.
Partie B.
Pour la suite de l’exercice, on admet que la fonction f est définie sur [0 ; +∞[ par :
f (x) = (x +1)e-0,5x.
1. a. Justifier que, pour tout réel x positif, f (x) = 2 (0,5x /e0,5x )+e-0,5x.
f(x) = x e-0,5x +e-0,5x = x / e0,5x +e-0,5x =2 (0,5x /e0,5x )+e-0,5x.
b. Calculer la limite de la fonction f en +∞.
En plus l'infini : e-0,5x tend vers zéro. 0,5x /e0,5x tend également vers zéro.
f(x) tend vers zéro.
2. Étudier les variations de la fonction f sur [0 ; +∞[ et construire son tableau de variations.
f '(x) = (-0,5x+0,5)e-0,5x.
Le signe de f '(x) est celui de -0,5x+1, le terme en exponentielle étant positif.
La dérivée s'annule pour x=1. f '(x) > 0 pour x <1 ( f(x) est croissante).
f '(x) < 0 pour x > 1 ( f(x) décroissante).
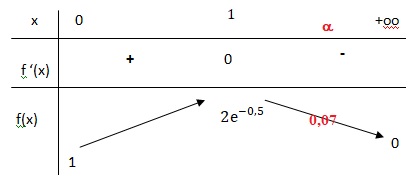
3. Démontrer que l’équation f (x) = 0,07 admet une unique solution α sur l’intervalle [0 ; +∞[.
Sur l’intervalle [0 ; 1[, f(x) est strictement croissante de 1 à 2e-0,5 ~1,213 . 0,07 n'appartient pas à [1 ; 2e-0,5 ].
Sur l’intervalle [1 ; +∞[, f(x) est strictement décroissante de 2e-0,5 ~1,213 à 0.
0,07 n'appartient pas à [ 2e-0,5; 0 ].
4. Donner l’arrondi de α à l’unité.
La calculatrice donne a ~ 10.
Partie C -Modélisation d’un tas de sable.
Dans cette partie, on considère que la courbe de la fonction f modélise le profil d’un tas de sable.
La longueur x et la hauteur f (x) sont exprimées en mètres.
Ainsi, le fait que f (0) = 1 signifie qu’à son extrémité gauche, la hauteur du tas de sable est de 1 mètre.
On souhaite que le tas de sable soit limité par deux murs comme indiqué sur le schéma ci-dessous.
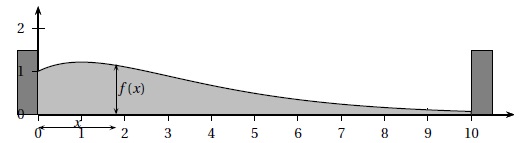
Le mur de gauche coïncide avec l’axe des ordonnées et le mur de droite est placé de telle sorte
que la hauteur de sable à cet endroit est de 7 cm.
1. Pourquoi le mur de droite doit-il être placé à environ 10 mètres du mur de gauche?
7 cm = 0,07 m et f(10) ~0,07.
2. Vérifier que la fonction G définie sur [0; 10] par G(x) = (−2x −4)e-0,5x est une primitive de la fonction g définie sur [0; 10] par g (x)= x e-0,5x.
On dérive G(x) en posant u = -2x-4 et v = e-0,5x.
u' = -2 ; v' = -0,5e-0,5x.
u'v+v'u = -2 e-0,5x-0,5(-2x-4)e-0,5x=x e-0,5x =g(x).
3. En déduire une primitive de la fonction f sur l’intervalle [0; 10].
f (x) = x e-0,5x+ e-0,5x = g(x) +e-0,5x.
Primitive de f(x) : F(x) = G(x) -2e-0,5x=(−2x −4)e-0,5x -2e-0,5x=(−2x −6)e-0,5x .
4. Pour
pouvoir créer un terrain de sport sur sable, on décide de niveler le
tas de sable, c’est à-dire de l’étaler à une même hauteur entre les
deux murs.
Quelle sera la hauteur du tas de sable une fois le nivellement réalisé?
Expliquer le raisonnement et arrondir le résultat au centimètre.
Surface du tas de sable : F(10)-F(0) =(−26)e-5 -(-6)= 6-26 e-5 ~5,82 m2.
Puis diviser par 10, distance des murs.
Hauteur du sable : 0,58 m.
|
...
|
|
|
....
|
Exercice 2. ( 5 points)
Les probabilités seront arrondies si nécessaire au millième.
Partie A.
Une antenne relais chargée d’acheminer des communications est exploitée par trois opérateurs :
l’opérateur A, l’opérateur B et l’opérateur C.
Par ailleurs, cette antenne utilise deux types de canal : le canal vocal (pour les communications téléphoniques) et le canal internet (pour les communications par texto ou par mail).
On dispose des données suivantes :
• 40% des communications passent par l’opérateur A;
25% des communications passent par l’opérateur B;
• 10% des communications passant par l’opérateur A utilisent le canal vocal ;
• 20% des communications passant par l’opérateur B utilisent le canal vocal ;
• 20% de l’ensemble des communications utilisent le canal vocal.
On choisit une communication au hasard et on considère les évènements :
• A : « la communication passe par l’opérateur A » ;
B : « la communication passe par l’opérateur B » ;
• C : « la communication passe par l’opérateur C » ;
• V : « la communication utilise le canal vocal ».
1. À l’aide des valeurs de l’énoncé, compléter les branches de l’arbre pondéré.
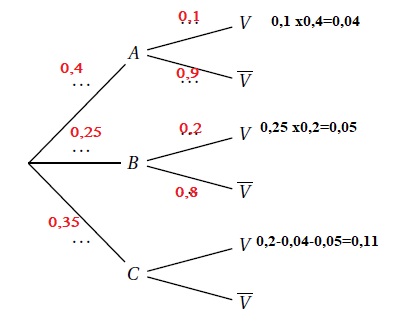
2. Calculer la probabilité que la communication passe par l’opérateur A et utilise le canal vocal.
P(A n V) =0,1 x 0,4 =0,04.
3. La communication passe par l’opérateur C. Quelle est la probabilité qu’elle soit acheminée par le canal vocal ?
0,2-0,04-0,05 = 0,11.
PC(V) = 0,11 / 0,35 ~0,314.
Partie B.
Cette antenne relais couvre une zone géographique bien définie appelée cellule. Dans cette cellule, les ressources radio sont limitées à 350 appels simultanés. Cela signifie qu’au-delà de 350 appels, l’antenne relais est saturée.
Dans cette cellule, 1 600 personnes possèdent chacune un téléphone mobile.
À un instant donné, on choisit au hasard une personne parmi les 1 600 personnes de la cellule.
On admet que la probabilité que cette personne passe un appel téléphonique est égale à 0,2.
On admet en outre que les 1 600 personnes de la cellule agissent indépendamment les unes des autres.
On note X la variable aléatoire égale au nombre de personnes passant un appel à un instant donné dans cette cellule.
1. Quelle est la loi de probabilité suivie par la variable aléatoire X ? On précisera ses paramètres.
Cette expérience aléatoire admet deux issues : la personne téléphone ( probabilité p = 0,8) ou bien elle ne téléphone pas.
Chaque expérience est réalisée dans les mêmes conditions.
X suit une loi binomiale de paramètres n = 1600 et p = 0,2.
2. Calculer l’espérance de la variable aléatoire X et interpréter le résultat.
E(X) = n p = 1600 x0,2 = 320.
En moyenne, 320 personnes passent un coup de téléphone.
3. Calculer la probabilité que l’antenne ne soit pas saturée.
Au delà de 350 appels, l'antenne est saturée.
La probabilité que l'antenne ne soit pas saturée est P(X < 350) ~0,971.
Partie C.
On considère une autre cellule dans laquelle le nombre de personnes passant un appel téléphonique au même moment est modélisé par une variable aléatoire Y suivant une loi normale d’espérance μ = 335 et d’écart-type σ inconnu,
1. On a constaté que, dans cette cellule, la probabilité que l’antenne soit saturée est 0,001 5.
On rappelle que l’antenne est saturée lorsque le nombre de personnes passant un appel téléphonique au même moment est supérieur à 350.
a. On a réalisé un croquis donnant l’allure de la courbe de la fonction densité de la variable aléatoire Y .
Hachurer sur cette annexe le domaine correspondant à la probabilité que l’antenne soit saturée.
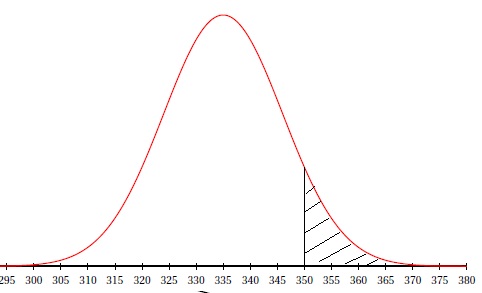
b. Justifier que la valeur de σ, arrondie à l’unité, vaut 5.
P(Y >350) = 0,0015 ; P(Y < 350) =1-0,0015 = 0,9985.
On pose Z = (Y-335) / s.
Z suit la loi normale centrée réduite.
Y < 350 équivaut à Z < 15 /s.
P (Z < 15 /s) =0,9985.
La calculatrice donne 15 /s ~2,9678 ; s ~5.
2. L’antenne dispose d’un mode « économie d’énergie » qui s’active lorsque moins de 330 personnes passent un appel téléphonique au même moment. Calculer la probabilité que l’antenne soit en mode « économie d’énergie ».
P(Y < 330) ~0,159.
|
Exercice3. ( 4 points)
PARTIE A
On considère l’équation suivante :
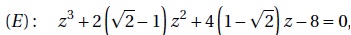
ayant pour inconnue le nombre complexe z.
1. Démontrer que, pour tout nombre complexe z,
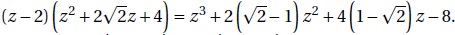
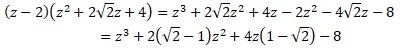
2. Résoudre dans C l’équation (E) en donnant ses solutions sous forme algébrique.
3. Écrire toutes les solutions de l’équation (E) sous forme exponentielle.
z-2=0 soit z1 = 2 ;z1 =2 exp(0).
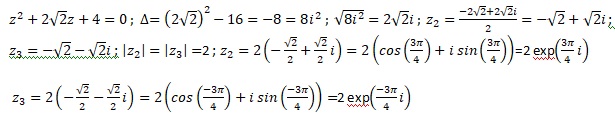
PARTIE B.
Dans cette partie, on cherche à déterminer les valeurs exactes de cos (3p/8) et sin ( 3p/8).
On munit le plan complexe d’un repère orthonormé direct.
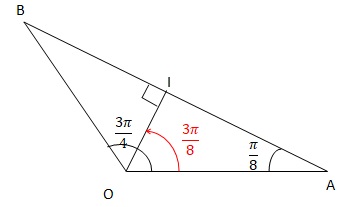
On considère les points A et B du plan complexe d’affixes respectives zA = 2 et zB = 2exp (i 3p/4) et I le milieu du segment [AB] d’affixe zI.
1. Démontrer que le triangle OAB est un triangle isocèle.
OA = |zA|=2.
zB = 2exp (i 3p/4)=2 ( cos3p/4) + i sin(3p/4))= -2½ +2½ i.
OB = |zB|=2.
OA = OB, le triangle OAB est isocèle.
2. Démontrer qu’une mesure de l’angle (u ; OI) est 3p/8.
3. Déterminer la forme algébrique de l’affixe zI puis le module de zI.
I est le milieu de AB. zI = (zA+zB) / 2 =(2-2½ +2½ i) / 2=(1-2½ / 2) + i 2½ / 2.
|zI|2=(1-2½ / 2)2+(2½ / 2)2=2-2½.
|zI|= [2-2½]½.
4. En déduire les valeurs exactes de de cos (3p/8) et sin ( 3p/8).
zI =|zI| exp(i3p/8)=[2-2½]½ ( cos(3p/8) + i sin(3p/8) )
On identifie : cos(3p/8) =(1-2½ / 2) /[2-2½]½.
sin(3p/8) =(2½ / 2) /[2-2½]½.
Exercice 4 ( 5 points).
Pour chacune des affirmations suivantes, indiquer si elle est vraie ou fausse en justifiant la réponse.
1. On considère la suite (un) définie par
u0 = 6 et pour tout entier naturel n, un+1 =0,75un +1.
Affirmation 1 : Pour tout entier naturel n, un = 2 x 0,75n +4. Vrai.
Initialisation : u1 =0,75 u0 +1 =0,75 x 6 +1 =5,5=2x0,751+4 ; la propriété est vraie au rang 1.
Hérédité : la propriété est supposée vraie au rang p.
up = 2 x 0,75p +4.
up+1=0,75up +1 =0,75(2 x 0,75p +4) +1 =2 x0,75p+1+3+1.
Conclusion: la propriété est vraie au rang 1 et héréditaire ; elle est vraie pour tout entier n.
2. Soit (tn) une suite géométrique de premier terme t0 = 2 et de raison 0,25.
On appelle Sn la somme des n+1 premiers termes de la suite (tn) , soit Sn = t0+t1+. . .+tn.
Affirmation 2 : La suite (Sn) a pour limite +∞. Faux.
tn = t0 x0,25n=2 x 0,25n ; Sn =t0(1-qn) / (1-q) =2(1-0,25n) / (1-0,25)=8(1-0,25n) /3.
Quand n tend vers plus l'infini, 0,25n tend vers zéro et Sn tend vers 8 /3.
3. On définit la suite (cn), pour tout entier naturel n non nul, par
cn = 1+cos(n) / n.
Affirmation 3 : La suite (cn) est convergente. Vrai.
-1 < cos(n) < 1 ; -1 / n < cos(n)/ n < 1/ n ; 1-1 / n < 1+cos(n)/ n < 1+1/ n ;
1-1 / n < cn < 1+1/ n ;
Quand n tend vers plus l'infini, 1 /n tend vers zéro.
D'après le théorème des gendarmes on peur dire que la suite cn converge vers 1.
4. Dans un repère orthonormé de l’espace, on considère les points A(1; 2; 0) , B(3; 0; 6) , C(6 ; −1 ; 9) et D(−4 ; 4 ; −6).
Affirmation 4 : Les droites (AB) et (CD) sont sécantes. Vrai.
Coordonnées du vecteur AB :(3-1 ; 0-2 ; 6-0) soit (2 ; -2 ; 6).
Coordonnées du vecteur CD :(-4-6 ; 4+1 ; -6-9) soit (-10 ; 5 ; -15).
Représentation paramétrique de la droite (AB) :
x = 2t+1 ; y = -2t+2 ; z = 6t avec t réel.
Représentation paramétrique de la droite (CD) :
x = -10k+6 ; y =5k-1 ; z = -15k+9 avec k réel.
Si les droites sont sécantes : 2t+1= -10k+6 (1) ; -2t+2 = 5k-1 (2) et 6t = -15k+9 soit t = -2,5k +1,5.
Repport dans (1) : 2(-2,5k +1,5)+1= -10k+6 ; 5k = 2 soit k = 0,4 et t =0,5
Repport dans (2) : -1+2=5 x0,4 -1 =2 ; c'est vrai.
Coordonnées du point d'intersection : 2 ; 1 ; 3.
5. L’espace est muni du repère orthonormé . Soit P le plan passant par A(1; 2; 0)et de vecteur normal n (6 ; 4 ; −1).
Soit D la droite de représentation paramétrique
x = t +1 ; y = −t −1 ; z = 2t +3 , , t ∈ R.
Affirmation 5 : Le plan P et la droite D ne possèdent aucun point commun. Vrai.
Equation cartésienne du plan P : 6x+4y-z+d = 0.
A appartient à ce plan : 6+8-0+d = 0 soit d = -14.
6x+4y-z-14 = 0.
Hypothèse : la droite et le plan se coupent :
6(t+1) +4(-t-1)-(2t+3)-14=0.
6t+6-4t-4-2t-3-14=0.
0 t-15 =0, imposible.
L'hypothèse est fausse.
|
|
|