Mathématiques,
concours Aspts Ouest
2018.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
1. Donner l’écriture la plus simple possible de :[2 /3 x racine carrée (3)]2.
2 ; 4 /3 vrai ; 3 ; 1 /3.
22 / 32 x 3 =4 /3.
2. 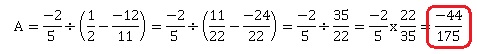
3. Quelle est la forme développée de : 2 x – ( x - 4)2 ?
x2 +10x -16; x2 +10x +16 ; -x2 -10x -16 ;- x2 +10x -16. Vrai
2x-(x2+16-8x) =2x-x2-16+8x = -x2+10x-16.
4. La factorisation de A = (2 x ̶ 1)2 ̶ (2 x ̶ 1) (4 x ̶ 7) est :
(2x-1)(-2x-6) ; (2x-1)(-2x+6) vrai ; (2x-1)(2x-6) ; (2x-1)(4x-7).
(2x-1)[ 2x-1-(4x-7)]=(2x-1)(-2x+6).
5. Le volume exact d’un cylindre de hauteur 5 cm et de rayon 2 cm est de :
10 p cm3 ; 7 p cm3 ; 20 p cm3 vrai ; 18 p cm3.
aire de base x hauteur = p22 x5 =20 p.
6. Dans un triangle ABC rectangle en A, on a AC = 6 cm et angle (C) = 45°. La longueur AB vaut :
3 cm ; 5 cm ; 6 cm vrai ; 7 cm.
tan 45 = AB / AC = 1 ; AB = AC =6 cm.
7. Le point A(3 ; -2) est sur la droite d'équation :
y = 2x-8 vrai ; y = x / 3 +1 ; y = -3x+1 ; y = 3x-2.
-2 =2 *3 -8 =-2.
8. Une diminution de 27% d’un nombre x se traduit par la fonction :
f(x) = -0,27 x ; g(x) = x-0,27 ; h(x) = 0,73 x vrai ; i(x) = 0,27 x.
9. J’ai acheté un meuble au prix de 460 euros après une réduction de 20%. Quel était le prix de ce meuble avant la remise ?
On note x le prix initial avant remise. 0,80 x = 460 ; x = 575 €.
480 € ; 500 € ; 575 € vrai ; 475 €.
10.
Une société loue des voitures 23 euros à la journée. Il faut payer 0,30
euros de plus par kilomètre parcouru. Quel est le prix, en fonction de
x , à payer à cette société de location ?
23 x+0,3 ; x(23 +0,3) ; 23 *0,3 x ; 23 +0,3 x vrai.
11. Les coordonnées du point d’intersection des droites d’équation y = -�2 x+1 et y =x / 3-2 sont :
(7 /9 ; -7 / 5) ; (9 /7 ; -5 /7) ; (-5/7 ; 9 /7) ; (5/7 ; -9/7).
-2x+1 = x/3 -2 ; 2x+x/3 =1+2 ; 6x /3 +x / 3 = 3 ; 7x / 3 = 3 ; x = 9 / 7.
y = -2 *9 / 7 +1 = -18 / 7 +7 / 7 = -11 / 7. ( 9 / 7 ; -11 / 7).
12. Deux élèves d’une même classe ont obtenu, aux 12 devoirs de l’année scolaire, les notes suivantes :
Elève A : 11 – 9 – 10 – 10 – 12 – 8 – 11 – 13 – 9 – 10 – 11 – 12
Elève B : 5 – 16 – 6 – 7 – 15 – 10 – 8 – 15 – 10 – 8 – 17 – 9
Les moyennes annuelles de chacun des élèves sont de :
A = 10 et B = 11 ; A =11,5 et B =10,5 ; A = 9,5 et B = 10,5 ; A =10,5 et B =10,5 vrai.
(11 +9 +10 +10+12 +8 +11 +13 +9 +10+11+12) / 12 =10,5.
(5 +16 +6 +7 +15 +10 +8 +15 +10 +8 +17 +9) /12 =10,5.
13.
Dylan dispose d’un jeu de 52 cartes tout à fait normal. Il y a bien 10
cartes numérotées de 1 à 10 ainsi qu’un valet, une dame et un roi dans
chaque couleur. Soit A l’événement « tirer un as ». Sophie tire une
carte au hasard. Quelle est la probabilité p(A) que cette
carte soit un as ? 2 /52 ; 1/13 vrai ; 3 /52 ; 2 /13.
4 /52 = 1 / 13.
14.
Dans une population, les groupes sanguins sont répartis en quatre
groupes : A, B, AB et O. D’autre part, ils sont répartis suivant le
facteur rhésus (+ et -). Ces répartitions (en %) sont indiquées dans le
tableau suivant :
groupes
|
A
|
B
|
AB
|
O
|
rhésus +
|
31,9
|
8,2
|
4,15
|
36
|
rhésus -
|
8,1
|
1,8
|
0,85
|
9
|
La probabilité qu’un individu, pris au hasard, soit du groupe B est de :
0,3 ; 0,1 vrai ; 0,2 ; 0,25. )(8,2 +1,8) / 100 =0,1.
15. La réduction de l’expression littérale 2x2-(x-1) est :
2x2-x-1 ; 2x2+x-1 ; 2x2-x+1 vrai ; 2x2+x-1.
|
|
|
16. Écrire sous la forme a racine carrée (b), avec b entier le plus petit possible, l’expression :
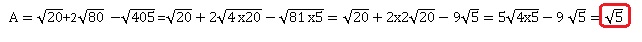
17. Dans le triangle ABC, rectangle en B, on donne : AB = 3 ; BC = 4 ; AC = 5.
Donc sin (C) = 4 /3 ; 3 / 4 ; 3 / 5 vrai ; 4 /5.
sin(C) = AB / AC = 3 / 5.
18.
Soit un cône de révolution de sommet S et de hauteur [SH]. La hauteur
de la génératrice de ce cône est SA = 6 cm et angle (ASH) = 60°. La
hauteur SH de ce cône est donc de : 3 cm vrai ; 2 cm ; 4 cm ; 6 cm.
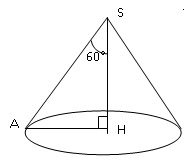
SH = AS cos(60) =6 x cos 60) = 3 cm.
19. ABCD est un rectangle et EFG un triangle équilatéral ; x désigne un nombre strictement supérieur à 3.
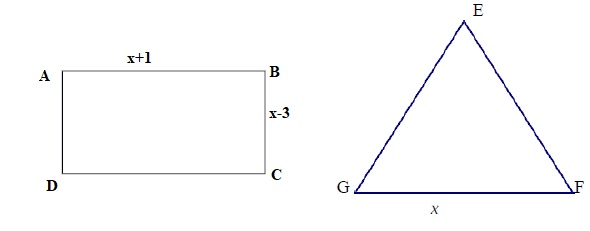
Le périmètre de ABCD et celui de EFG en fonction de x sont :
Périmètre du rectangle : 2(x+1 +x-3) =4x-4 ; périmètre du triangle : 3x.
2(x+1)(x-3) et x3 ; 4(x-1) et 3x vrai ; (x+1)(x-3) et x3 ; (x+1)(x-3) et 3x.
20. L'écriture scientifique de :4 x10-6 x3 x10-2 / (6 x10-5 x5 x102) est :
0,4 10-5 ; 4 10-5 ; 4 10-6 vrai ; 4 107.
4 x 3 /(6 x5) x10-6-2+5-2= 2 /5 10-5 =0,4 10-5 = 4 10-6.
21.
La structure métallique de la tour Eiffel a une masse de 7 300 tonnes.
On considère que la structure est composée essentiellement de fer.
Sachant qu’un atome de fer a une masse de 9,352×10-26 kg, combien y a-t-il d’atomes de fer dans la structure ? 9,352 1031 ; 7,8 1031 vrai ; 7,8 10-26 ; 78 1032.
7300 x 1000 / (9,352 10-26) =7,8 1031.
22. Le PGCD de 1820 et 5733 est : 100 ; 81 ; 91 vrai. ; 90.
1820 = 22 x5 x 91 ; 5733=32 x7 x91.
23. La pyramide du Louvre est une pyramide régulière dont la hauteur mesure 21 m et dont la base carrée a 34 m de côté.
Son volume est donc égal à (en m3) :
4000 ; 7160 ; 6780 ; 8092 vrai .
aire de base x hauteur / 3 = 34 x34 x21 /3 = 34 x34 x7 =8092 m3.
24. ABC est un triangle rectangle en A tel que AB = 7 cm et AC = 5 cm. M est un point de
[AC]. On note x = AM. N est un point de [AB] tel que (MN) et (BC) sont parallèles.
Quelle est l’expression de AN en fonction de x ?
1,4 x vrai ; 2x+1 ; 3x ; 1,5 x.
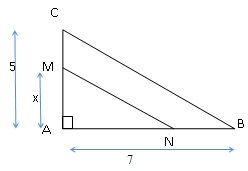
x /5 = AN / 7 ; AN = 7x /5 = 1,4 x.
25. Un
triangle a des côtés qui mesurent x+4 cm , x cm et 9 cm. Le côté de x+4
est le plus long. Pour que ce triangle soit rectangle, les côtés
doivent mesurer :
6,15 ; 8,15 et 9 cm ; 8,125 ; 9 et 12,125 cm vrai ; 7 ; 9 et 12 cm ; 9 ; 10,5 et 13,15 cm.
(x+4)2 = x2 +92 ; x2 +16 +8x =x2 +81 ; 8x = 81-16 = 65 ; x = 65/8 =8,125.
8,125 ; 9 ; 12,125 cm.
26. Le nombre entier dont la différence entre son quotient par 2 / 3 et son produit par 2 / 7 est égal à 221 est :
180 ; 181 ; 182 vrai ; 183.
Soit x le nombre cherché : 3 x / 2 -2x / 7 = 221 ; 21 x / 14 -4x / 14 = 221 ; 17 x / 14 = 221 ; x = 221 x14 / 17 = 182.
27. Voici un programme de calcul :
Choisir un nombre
Multiplier ce nombre par 2
Ajouter 5
Multiplier le résultat précédent par 3
Soustraire 8 à ce produit.
On note x le nombre de départ. Quelle est la fonction qui associe à x le résultat obtenu avec ce programme ?
6x-7 ; -6x+7 ; 6x+7 vrai ; -6x-7.
2x ; 2x+5 ; 3(2x+5) ; 3(2x+5) -8 =6x +7.
28.
Une somme de 1 850 euros est constituée uniquement de billets de 20
euros et de billets de 50 euros. Il y a exactement 58 billets.
Combien y a-t-il de billets de 20 euros et de billets de 50 euros ?
23 et 35 ; 20 et 30 ; 35 et 23 vrai ; 30 et 40.
On appelle x le nombre de billets de 20 € : 20x +50(58-x) =1850.
-30x +50 x58 = 1850 ; 30 x = 2900 -1850 =1050 ; x = 1050 / 30 = 35.
29. Soit f ( x ) = -2x (2 x+3) -4 . L’image de 4 √2 par cette fonction est :
132 +24√2 ; -132 -24√2 vrai ; -132 +24√2 ; 132 -24√2 ;
-4 √2 * 2(2 * 4 √2 +3)-4 = -8 √2(8 √2 +3)-4 = -128-4- 24 √2 = -132-24 √2.
|
|
|
|
30. On considère l’agrandissement de coefficient 2 d’un rectangle ayant pour largeur 5 cm et pour longueur 8 cm.
Quelle est l’aire du rectangle obtenu ? (en cm2).
40 ; 100 ; 80 ; 160 vrai.
10 x16 = 160 cm2.
31. Soit la fonction g ( x )= -3( x -√2)2+4√2 . Quelle est l’image par g du réel -2 ?
18-8√2 ; -18-8√2 vrai ; -18 +8√2 ; 18 +8√2.
-3( -2 -√2)2+4√2 = -3(4 +2 +4√2) +4√2 = -18 -12√2 +4√2 = -18 -8√2.
32. Quels sont les antécédents par f ( x ) = (2 x+3)(2-x) du réel 0 :
2 et -1,5 vrai ; -2 et -1,5 ; 2 et 1,5 ; -2 et 1,5..
(2 x+3)(2-x) =0 soit 2x+3 = 0 ; x = -1,5 et 2-x=0 soit x = 2.
33. Les côtés d’un hexagone régulier inscrit dans un cercle de 3 cm de rayon mesurent chacun :
moins de 3 cm ; plus de 3 cm ; aucune de ces réponses ne convient ; exactement 3 cm vrai.
34. Les droites (KC) et (JB) sont sécantes en A. KA = 2,8 ; AC = 4,2 ; JA = 2 ; AB = 3.
Je peux affirmer que : (BK) // (CJ) ; (BC) // (KJ) vrai ; (JK) //(BC) vrai ; (JB) //(KC).
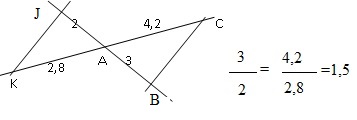
35.
Emmanuel part en vacances en Espagne. Pour cela, il doit parcourir 620
km. Il fait une halte le premier jour et a parcouru 3 / 4 du trajet. Il
reprend ensuite la route mais ne parcourt qu’un cinquième du trajet
restant. Que lui reste-t-il à parcourir pour arriver à destination ? (
en km)
124 vrai ; 130 ; 125 ; 100.
620 x3 / 4 =465 ; 620 -465 = 155 ; 155 / 5 =31 ; 620 -465 -31 =124 km.
36. Quelle est la médiane de la série suivante ?
valeurs
|
12
|
14
|
20
|
25
|
43
|
47
|
effectif
|
5
|
7
|
14
|
5
|
2
|
32
|
effecti cumulé croissant
|
5
|
12
|
26
|
31
|
33
|
65
|
41 ; 43 vrai ; 40 ; 42.
Effectif total : 65. 65 / 2 =32,5.La médiane est la 33ème valeur soit 43.
37.
On choisit une urne au hasard puis on tire une boule de cette urne.
Dans l’urne n°1 se trouvent 3 boules bleues et 1 boule rouge. Dans
l’urne n°2 se t rouvent 3 boules rouges, 1 jaune et 1 bleue. La
probabilité pour que la boule tirée soit bleue est :
0,1 ; 3 /8 ; 15 /4 ; 19 /40 vrai.
Probabilité de tirer une boule bleue de l'urne n°1 : 3 /4.
Probabilité de choisir l'urne n°1 : ½
Probabilité de tirer une boule bleue de l'urne n°2 : 1 / 5 ; 3 /4 + 1 /5 = 15 / 20 + 4 / 20 = 19 / 20.
Probabilité de choisir l'urne n°2 : ½.
0,5 ( 3 /4 + 1 /5 )= 0,5 (15 / 20 + 4 / 20 ) = 19 / 40.
38. La
Terre est assimilée à une sphère de rayon 6 370 km. On considère le
plan perpendiculaire à la ligne des pôles (N-S) et équidistant de ces
deux pôles. L’intersection de ce plan avec la Terre s’appelle
l’équateur. La longueur de l’équateur arrondie au km près est donc de :
40024 km vrai ; 41 000 km ; 45 000 km ; 35003 km.
2 p R = 2 x3,14 x6370 ~40 024 km.
39. Le saut à ski comprend 3 étapes distinctes dont la descente de la piste d’élan avant de s’élancer dans les airs.
Lors d’une compétition, un présentateur annonce au micro « le skieur a
dévalé la piste d’élan en 5 secondes. Sa vitesse moyenne sur cette
longueur est au moins de 70 km/h ».
L’affirmation du présentateur est-elle vraie sachant que l’inclinaison
est de 45° et que la piste commence à une altitude de 1989 m pour finir
à une altitude de 1900 m ?
oui vrai ; non, sa vitesse est de 45 km /h ; non sa vitesse est de 75 km / h ;
je n'ai pas assez d'informations pour calculer sa vitesse moyenne.
Longueur de la piste ( 1989 -1900 ) / sin (45) =89 / 0,707 ~126 m ; 126 / 5 ~25 m/s ou 25 x3,6 ~91 km / h.
40. Laquelle de ces quatre figures trace le lutin quand on lance le programme ci-dessous.
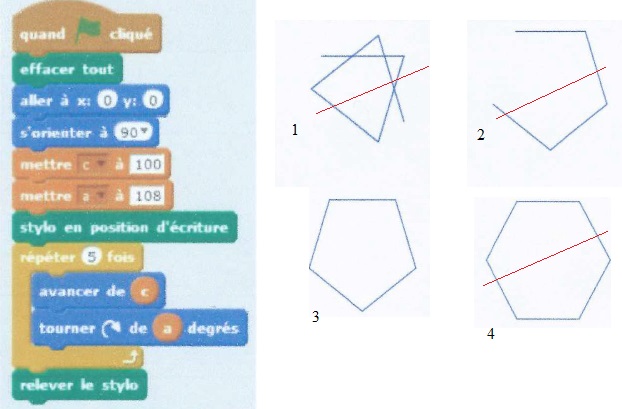
|
|
|