......
.....
|
|
|
Système
masse-ressort.
On suspend une masse m à un ressort veertical de raideur k et de
longueur L0. On effectue une étude statique puis une étude
dynamique.
masse m (fois 10-2
kg)
|
20
|
40
|
60
|
80
|
100
|
allongement x (fois 10-2
m)
|
4,0
|
8,1
|
12,2
|
16,2
|
20,2
|
durée de 10
oscillations (s)
|
4,06
|
5,75
|
3,95
|
8,03
|
8,96
|
Etude statique.
1. Exprimer
l'allongement x en fonction de L0 et Léquilibre.
x=Léquilibre - L0.
2. A l'aide
d'un graphique, déterminer la raideur k.
A l'équilibre le poids compense la tension du ressort. mg = kx ; m = k
/g x.
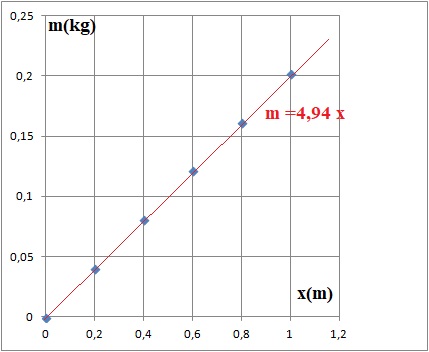
4,94
= k / g ; k = 4,94 x9,81 ~48,4 N m-1.
Etude dynamique.
a. Faire le
bilan des forces qui agissent sur le ressort.
Poids de la masse accrochée, verticale vers le bas ; tension du
ressort, verticale vers la position d'équilibre.
b. Montrer
que l'équation différentielle qui régit le mouvement du solide s'écrit
: m x" +kx = 0.
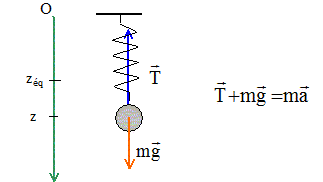
Ecrire la seconde loi de
Newton sur l'axe Oz : -k(z-L0)+mg=mz"
-k(z-zéq +zéq -L0)+mg = mz" ; -k(z-zéq
) -k(zéq -L0)+mg = mz"
Or k(zéq -L0)= mg d'où : -k(z-zéq ) =
mz".
On choisit la position d'équilibre comme nouvelle origine en posant u =
z-zéq :
il vient : -ku = mu" soit u" +k/m u= 0 ; u"+w02u
= 0 (1) avec w02 = k/m.
c. Montrer
que la solution de cette équation est x(t) = Xm cos (2pt / T0). T0
est la période de l'oscillateur.
x'(t) = -Xm 2p/ T0 sin (2pt / T0) ; x" = -Xm
(2p
/ T0 )2 cos (2pt / T0) = -w02 Xm cos (2pt
/ T0).
Repport dans (1) : -w02 Xm cos (2pt / T0)+ w02
Xm
cos (2pt
/ T0) =0 est vérifié quelque soit le temps.
d. En déduire
l'expression de T0.
T0 = 2p(k
/ m)½.
e.1.
Déterminer l'expression de la vitesse puis celle de l'énergie cinétique.
x'(t) = -Xm 2p/ T0 sin (2pt / T0) : Ec = ½mXm2 (2p/ T0 )2sin2 (2pt / T0).
e.2. On donne
les expressions de l'énergie potentielle élastique et de l'énergie
potentielle de pesanteur.
EPe = 0,5 k (mg / k +x)2 ; Epp = -mgx.
Compléter le tableau suivant.
t(s)
|
0
|
0,25 T0
|
x(m)
|
Xm
|
0
|
v(m/s)
|
0
|
-Xm 2p/ T0 =-Xm
w0.
|
Ec (J)
|
0
|
½m(Xm w0)2
|
| EPe (J) |
0,5 k (mg / k +Xm)2 |
0,5 (mg)2
/ k
|
| Epp (J) |
-mgXm |
0
|
Em(J)
|
0,5 k (mg / k +Xm)2 -mgXm |
½m(Xm
2p/ T0)2
+0,5 (mg)2 / k |
..
|
|
|
Numériser un son.
Les
données stockées sur un CD sont échantillonnées en 16 bits avec une
fréquence d’échantillonnage de 44,1 kHz ; de même sur un DVD audio. Sur
internet, où l’essentiel est que les fichiers soient peu volumineux et
où la qualité du son est moins importante puisque celui-ci n’est pas
écouté sur du bon matériel, on trouve des formats d’échantillonnage à
8 bits et/ou 22,05 kHz. La voix occupe un intervalle de fréquences
beaucoup plus réduit, le téléphone ne nécessite donc pas de fréquences
d’échantillonnage aussi élevées que 44,1 kHz. Dans la pratique, on se
contente de 8 kHz et de 8 bits. De même, la radio numérique se contente
de 22 kHz et 8 bits en modulation d’amplitude, et de 32 kHz 16 bits en
FM (ce qui permet davantage de programmes musicaux). Évidemment, on
pourrait utiliser plus de 16 bits et une fréquence d’échantillonnage
plus grande que 48 kHz. Mais cela occuperait encore plus de mémoire, et
personne, même pas les professionnels, n’entendrait la différence…
Le
MP3 ne correspond pas à une fréquence d’échantillonnage ou à un nombre
de bits moins élevé, c’est un algorithme de compression. La musique est
d’abord échantillonnée en qualité CD, puis un algorithme enlève un
certain nombre de données qui correspondent à des éléments que l’on
n’entend pas sur un équipement audio multimédia classique. Mais sur un
équipement de grande qualité, la différence entre la qualité CD et la
qualité MP3 s’entend !
Lorsque
l’on veut stocker une information sur un support numérique (CD,
ordinateur…), il faut convertir le signal analogique (signal sonore,
électrique, lumineux…) en un signal numérique. On doit donc utiliser un
dispositif de conversion analogique/numérique (Convertisseur Analogique
Numérique, CAN). La qualité de cet échantillonnage dépend
essentiellement de deux paramètres, la fréquence d’échantillonnage et
le nombre de bits du convertisseur.
Quelle fréquence d'échantillonnage choisir ?
On enregistre sur un ordinateur un signal
électrique sinusoïdal (analogique) de 50 Hz délivré par un GBF
(Générateur de Basses Fréquences) que l’on fait parvenir à une
interface d’acquisition. Celle-ci contient un CAN qui va effectuer la
conversion en signal numérique que l’ordinateur peut stocker et
traiter. Comme on le sait, la première étape de la conversion consiste
à échantillonner.
1 Définir la fréquence du signal étudié. En déduire sa période.
La fréquence est égale au nombre de périodes par seconde. T = 1 /50 =0,02 s = 20 ms.
2. Définir la période d’échantillonnage Te ainsi que la fréquence d’échantillonnage Fe correspondante.
La période d'échantillonnage est la durée entre 2 mesures.
La fréquence d'échantillonnage est égale au nombre de mesures effectuées en 1 s.
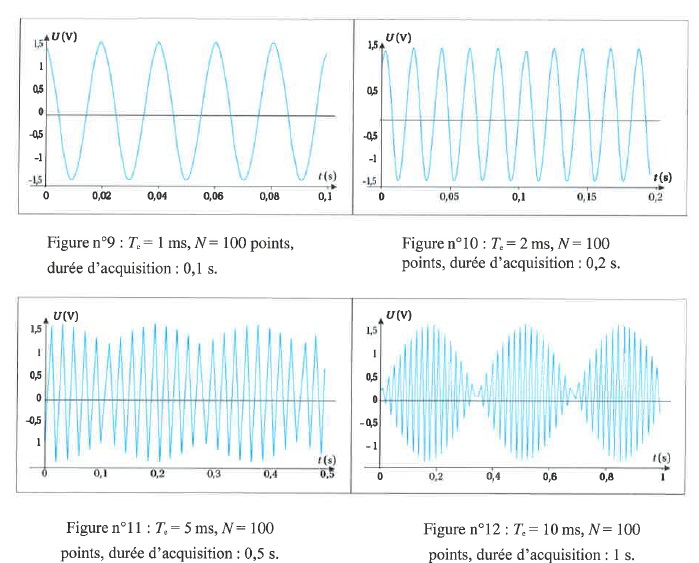
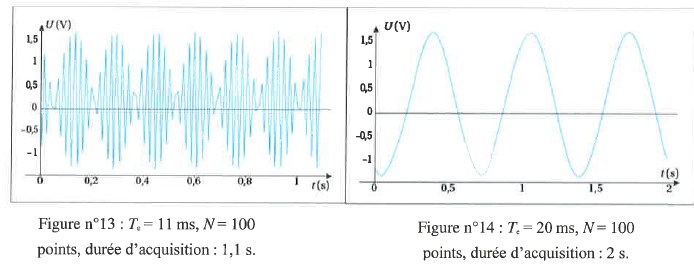
Les courbes suivantes ont toutes été réalisées à
partir du même signal (50 Hz), mais avec des fréquences
d’échantillonnage différentes.
3. Quelle relation existe entre Te, la durée totale d’acquisition et N le nombre de points acquis ?
Durée totale d'acquisition = N Te.
4. Au regard simplement de la forme des signaux,
lesquels retenez-vous ? Quels sont les deux graphiques qui permettent
de mieux restituer le signal délivré par le GBF ?
Figures :9 ; 10 ; 14 : les signaux sont sinusoïdaux.
On exclut la figure 14, la période ne correspond pas à 20 ms.
5. Déterminer le nombre d’échantillons prélevés pour
une période du signal dans chacun des cas. Conclure sur le choix du
nombre de points par période, et de la fréquence d’échantillonnage à
choisir.
Figure 9 : 100 points prélevés en 0,1 s soit 20 points en une période ( 0,02 s).
Figure 10 : 100 points prélevés en 0,2 s soit 10 points en une période ( 0,02 s). La figure est un peu déformée.
Il faut choisir un nombre de points assez grand par période ( au moins
10).Mais un nombre de points trop grand conduit à un fichier numérique
de trop grande taille.
Conversion analogique numérique.
On
se propose de numériser la tension associée à un son ; cette tension
analogique est visualisée sur l’écran d’un oscilloscope, reproduit
ci-dessous.
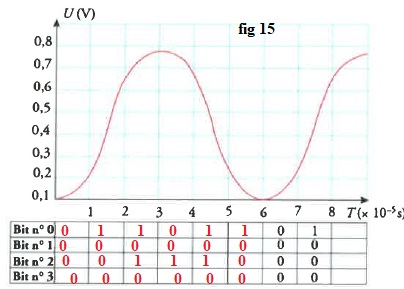
Le CAN est un convertisseur 4 bits.
La tension de référence est égale à 1,6 V (non inclus). La fréquence d’échantillonnage est 100 kHz.
1.Quelle est la valeur de la période d’échantillonnage ?
Te = 1 / (100 x103) = 10-5 s.
2. Quelle est la valeur du « pas » du convertisseur (en volt) ?
pas = 1,6 / 24 =0,1 V.
3. Pour chaque échantillon, le convertisseur garde
en mémoire la valeur de la tension qu’il capte au début de
l’échantillonnage. Par exemple, dans l’intervalle 7 × 10–5 s <t < 8 × 10–5 s, la valeur de la tension mémorisée est 0,14 V. Cette valeur correspond à (1,4 × pas) du convertisseur, le convertisseur ne prend en compte que la partie entière du nombre de « pas » et renvoie la valeur (1)2, soit 0001.
Compléter
le tableau de la figure 15 donnant les valeurs binaires renvoyées par
le convertisseur pour les 6 premiers échantillons.
Écrire
sur une ligne la suite des valeurs « 0 » ou « 1 » enregistrées à la
sortie du convertisseur, sachant que pour chaque quartet la première
valeur enregistrée est celle correspondant au bit des unités (bit n° 0).
0 < t < 1 10-5 s : U = 0 ; 0000.
1 10-5 s < t < 2 10-5 s : U = 0,12 arrondi à 1 ; 0001.
2 10-5 s < t < 3 10-5 s : U = 0,55 arrondi à 5 ; 0101.
Écrire
sur une ligne la suite des valeurs « 0 » ou « 1 » enregistrées à la
sortie du convertisseur, sachant que pour chaque quartet la première
valeur enregistrée est celle correspondant au bit des unités (bit n° 0).
Codage de t = 0 à 8 10-5 s : 0000 0001 0101 0110 0100 000 0001 0101.
Conversion d'un fichier son.
On a enregistré un fichier « son 1 » de 3 s. Puis ce fichier a été ensuite enregistré sous différents paramétrages.
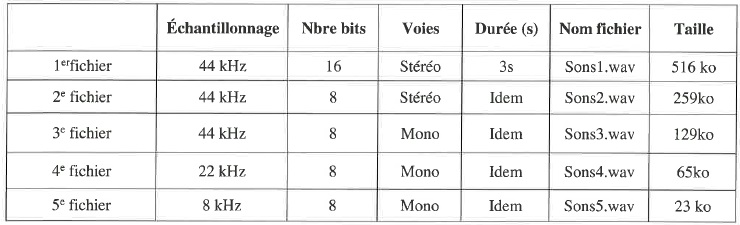
Etude de la taille des fichiers.
1. L’ordre de grandeur est-il de 2 entre les 1er et 2e fichiers ? Les 2e et 3e fichiers ? Les 3e et 4e fichiers ? Justifier.
Entre les 1er et 2e fichiers : le signal a été enregistré avec 2 fois moins de bit ; l'ordre de grandeur est de 2.
La taille du fichier est proportionnelle au nombre de bits.
Entre les 2e et 3e fichiers : le signal est enregistré en mono et non en stéréo. La taille est divisée par 2.
Entre les 3e et 4e fichiers
: mono sur 8 bits avec une fréquence d'échantillonnage 2 fois
plus petite ( moins d'informations sont prélevées). On divise par 2 la
taille du fichier.
2. Quel est le rapport des tailles des fichiers entre les 4e et 5e fichiers ? Quelle est la raison ?
La taille du fichier est proportionnelle à la fréquence d'échantillonnage. 22 /8 =2,75 ; 65 /23 ~2,8.
Calcul théorique de l'encombrement du premier fichier son.
1. Le nombre de bits n doit être exprimé en nombre d’octets utilisés. Quel est le nombre d’octets pour n bits de votre échantillon ?
16 bits correspondent à 2 octets.
2. Une seconde de son enregistré dépend du nombre fE d’échantillons par seconde. Quel est le nombre d’échantillons en octets par seconde ? Pour une acquisition de durée totale t, quel est alors l’encombrement ?
fE = 44 kHz ; 44 000 échantillons par seconde.
Pour 2 octets par échantillon par seconde : 44 000 x2 =88 000 octets par seconde.
88 000 x3 = 264 000 octets en 3 s.
3 . La taille finale de l’extrait dépend du nombre N de
voies. En déduire la formule littérale générale permettant de trouver
la taille d’un fichier son. Vérifier ce calcul sur votre premier
fichier enregistré.
Est-ce cohérent ?
N = 2 voies.
Taille d'un fichier son : Fe n t N /8 octets.
Ou bien Fe n t N / (8x 1024) ko.
44 000 x16 x 3 x3 / (8 x1024) = 516 ko.
4. Calculer l’encombrement d’une chanson de
4 minutes à 44 kHz et 16 bits en stéréo. Présenter votre résultat dans
une unité adaptée.
Combien de chansons peut-on graver sur un CD-Rom de 750 Mo ?
516 x 4 x60 /3 = 41 280 ko = 41,28 Mo.
750 / 41,28 ~18.
|





