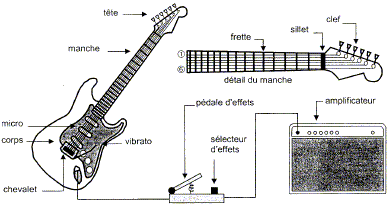
La guitare électrique, trajectoire d'un wagonnet, Concours audioprothésiste Nancy 2019. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. ...... ..... . . . . La guitare électrique. La guitare électrique est composée de six cordes métalliques de longueur utile entre le sifflet et le chevalet 63,0 cm. L'accord traditionnel à vide est, de la note la plus grave à la plus aigue : mi1, la1, ré2, sol2, si2, mi3. Le chiffre en indice indique le numéro de l'octave. Une corde est dite " à vide" lorsqu'elle vibre sur toute sa longueur. Les fréquences des notes produites à vide par les cordes pincées de la guitare sont les suivantes : n° de la corde 1 2 3 4 5 6 note mi1 la1 ré2 sol2 si2 mi3 fréquence (Hz) 82,4 110 146,8 196 246,9 329,6 Une guitare basse électrique fonctionne sur le même principe avec des notes plus graves. La diversité des effets possibles avec une guitare électrique en fait un instrument polyvalent et riche musicalement. Paarmi la multitude d'effets on peut citer l'effet "wha wha" popularisé par Jimi Hendrix. Analyse temporelle d'une note de musique. Un système d'acquisition de données permet l'enregistrement et la visualisation des tensions électriques associées aux différentes notes que peut produire une guitare électrique. 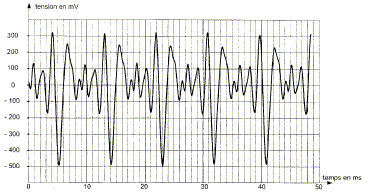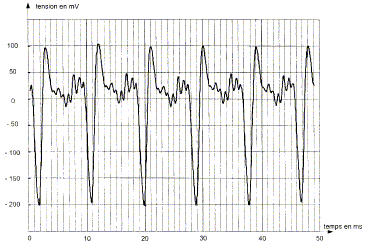Les figures suivantes présentent les signaux enregistrées pour la même note de musique jouée par une guitare électrique et par une guitare basse. 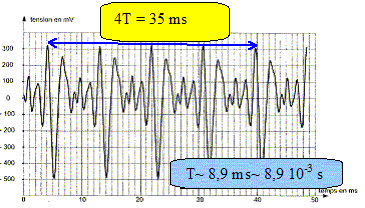guitare électrique : guitare basse : Quelle est la qualité physiologique commune des deux sons enregistrés ? Nommer la grandeur physique associée. La hauteur ou fréquence du fondamental. Mesurer cette grandeur physique et en déduire la note de musique jouée. f = 1/T = 1/ 8,9 10-3 = 1,1 102 Hz ( la1). Quelle qualité physiologique permet de distinguer les deux sons ? Les deux courbes ont des allures différentes : les sons ne possèdent pas les mêmes harmoniques. Mode propre de vibration de la corde 6.  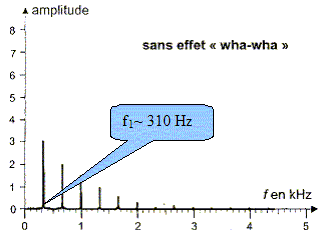L'analyse spectrale permet après une acquisition informatisée et un traitement numérique de révéler la "signature" acoustique d'un son en faisant apparaître les composantes de basses fréquences ( 80 Hz - 900 Hz) et de fréquence élevées ( 900 Hz - 16 kHz ) qui le caractérisent. La figure suivante correspond au spectre en fréquence du son produit par la corde n°6 d'une guitare électrique jouée à vide.   Déterminer la valeur approchée de la fréquence f1 du fondamental de se son. Vérifier la cohérence avec la donnée du texte. 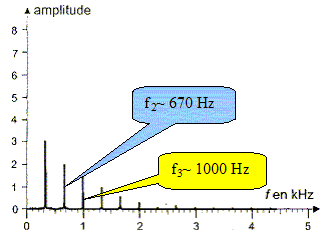f1 ~ 0,31 kHz ; le texte indique 329 Hz : les valeurs étant assez proches, elles sont cohérentes. Déterminer les valeurs approchées des fréquences f2 et f3 des harmoniques immédiatemment supérieures au fondamental. Le sillet et le chevalet de la guitare sont séparés par une distance L==63,0 cm. La condition entre l et L traduisant la condition d'existence d'une onde stationnaire entre ces deux points est : 2L= kl où k est un entier positif. En déduire l'expression de la longueur d'onde l du mode fondamental. Calculer cette longueur d'onde. k =1 ; l = 2 L =2 x0,63 = 1,26 m. Ecrire la relation entre la longueur d'onde l, la célérité c et la fréquence f d'une onde sinusoïdale. En déduire la célérité des ondes dans cette corde. f1 ~ 3,3 102 Hz l = c/f ; c = l f 1,26*3,3 102 c =4,2 102 m/s En jouant, le guitariste bloque la corde sur l'une des barettes placées sur le manche, appelées frettes, afin d'obtenir la note désirée. Quel est l'effet produit sur le son ? Justifier. La longueur de la corde diminue : l = 2L en conséquence la longueur d'onde du fondamental diminue. l = c/f : la célérité étant constante, la fréquence du fondamental augmente Le son devient plus aigu. 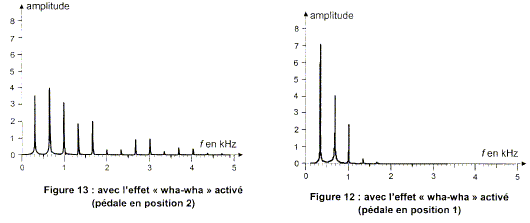L'effet "wha wha" Les figures suivantes représentent les spectres en fréquences du son de la figure ci-dessus sur lequel on a appliqué l'effet pour deux positions extrèmes de la pédale d'effets.   En comparant ces trois spectres, préciser quels sont les effets de la pédale "wha wha" sur les propriétés physiologiques du son produit dans les mêmes conditions d'attaque de la corde. La fréquence du fondamental est inchangé : la hauteur du son n'est pas modifiée. Le nombre d'harmoniques et leurs amplidudes relatives sont différentes : le timbre du son et le niveau sonore sont donc modifiés. Etude des niveaux sonores. 1. Le seuil de la douleur pour l'oreille humaine se situe vers 130 dB. Quelle est l'intensité acoustique correspondante ? I = 10-12 x 1013 =10 W m-2. 2. De combien augmente le niveau en décibel quand l'intensité acoustique double ? 10 log(2) = 3 dB. 3. Les deux guitares ( bassse et électrique) génèrent respectivement des niveaux sonores 100 dB et 103 dB. Calculer les intensités acoustiques correspondante. I1 = 10-12 x1010 = 10-2 W m-2 ; I2 = 10-12 x1010,3 = 10-1,7 =2 10-2 W m-2 . Calculer le niveau sonore total. Itotal =3 10-2 W m-2 ; L = 10 log(3 10-2 /10-12) =104,7 ~105 dB. Combien faut-il de guitares électriques pour atteindre le seuil de la douleur lorsqu'elles jouent ensemble ? N : nombre de guitares ; n I2 =0,02 n W m-2  ; 130 = 10 log(0,02n / 10-12) ; 13 = log( 2 1010 n) ; 1013 = 2n 1010 ; n = 500. ... . II Trajectoire d'un wagonnet. Le wagonnet  est initialement au repos en A. On le lance sur la piste ACD en faisant agir sur lui le long de la partie AB, une force horizontale F de valeur constante. Les portions AC et CD sont dans le même plan vertical. Les frottements sont négligés. Etude du mouvement entre A et B. 1. Déterminer l'accélération du wagonnet. Le poids et l'action du plan se compensent. La seconde loi de Newton conduit à : a = F / m, direction horizontale, sens vers la droite. 2. Déterminer l'expression de la vitesse en fonction de F, m et x, la distance parcourue. Th  de l'énergie cinétique : ½mv2 -0 = F x ;  v = (2Fx / m)½. 3. Donner l'expression de la vitesse en B. vB = (2Fl / m)½. Etude du mouvement entre B et C. 1. Déterminer l'accélération du wagonnet. Le poids et l'action du plan se compensent. F est nulle. Le wagonnet est speudo-isolé et son accélération est nulle. 2. Quelle est la vitesse du wagonnet en C ? Sur BC le mouvement est rectiligne uniforme. vB =vC= (2Fl / m)½. Etude du mouvement entre C et D. 1. Faire l'inventaire des forces agissant sur le wagonnet. Poids : verticale vers le bas. Action du support, perpendiculaire au support, dirigé vers O. 2. Appliquer la seconde loi de Newton et en  déduire les expressions de dv /dt et v2 /r. Suivant l'axe t : m dv / dt = -mg sin q ; dv /dt = -g sin q. Suivant l'axe n : mv2 / r = R -mg cos q ; v2 / r = R/ m -g cos q . 3. Montrer que v2 -vC2 = 2g r (cos q-1) est en accord avec l'expression de dv/dt. Conservation de l'énergie mécanique : ½mv2C =½mv2 + mgl(1-cosq). v2C = v2 + 2g r(1-cosq) ; v2 -v2C = -2g r (cos q-1). Dériver par rapport au temps : 2 v dv /dt = 2g r sin q dq /dt ; or v = - r dq /dt ; dv /dt = -g sin q.