QCM Physique: chute, radioactivit�, optique, concours Orthoptie Lille 2014.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicit�s adapt�es � vos centres d’int�r�ts.

.
.


Chute.
On consid�re la chute d'un corps sph�rique dans l'air. On n�glige les frottements de l'air.
Question 1
Parmi les �l�ments suivants, lequel n'influence pas la vitesse d'arriv�e au sol ?
A - sa masse. Vrai. B. la hauteur de chute. C. La dur�e de la chute. D. sa vitesse initiale. E. la valeur du champ de pesanteur.

2. Soit une boule sph�rique de 500 g tombant d'une hauteur de 80 cm avec une vitesse initiale nulle. Quelle est l'ordre de grandeur de la dur�e de la chute  g = 10 m s-2.
0,8 = 5 t2 ; t = (0,8 / 5)� =0,4 s.
A - 0,1 s.  B. 0,2 s. C. 0,4 s. Vrai.  D. 1 s. E. autre valeur.

3. Quelle est approximativement la vitesse d'arriv�e au sol ( en m /s).
v = 10 t = 10 x0,4 = 4 m /s.
A - 1.  B. 2. C. 4. Vrai.  D. 6. E. autre valeur.

On laisse tomber une bille d'acier ( masse volumique 7,5 g cm-3) de 1 cm de rayon dans la glyc�rine ( masse volumique 1,25 g cm-3). Lors de la chute, il se cr�� un �quilibre entre la force de pesanteur P ( g = 9,9 m s-2) et les forces s'y opposant, li�es au principe d'Archim�de ( F) et � la viscosit� (f). On filme la chute de la bille d'acier dans la glyc�rine � la cadence de 25 images par seconde. Entre deux images successives, la distance parcourue par la sph�re dans la glyc�rine est de 5 cm.

 4. Quelle est le poids de la bille ?
Volume : 4 / 3 x3,14 x13 ~4,2 cm3 ; masse 4,2 x7,5 ~31 g. Poids = 0,031 x10 ~0,31 N.
A - 3,1 10-1 Vrai.  B. 3,1 10-2. C. 3,1 10-3  D. 3,1 10-4. E. autre valeur.
.
5
Lorsque la vitesse de la chute dans la glyc�rine devient constante et que les forces sont alors �quilibr�es, la force f est proportionnelle � certains param�tres. Quelle proposition est inexacte ?
A - volume de la bille ; B. masse de la bille ; inexacte.
C. diff�rence  des masses volumiques de l'acier et de la glyc�rine.
D. � la diff�rence entre la masse de la bille et celle d'un volume identique de glyc�rine.
E. � la diff�rence entre le poids de la bille et celui d''un volume identique de glyc�rine.

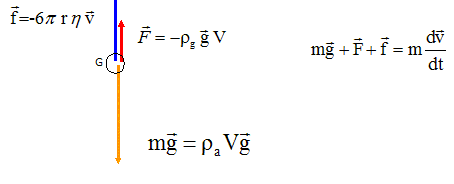
6. Quelle est la valeur approximative de la force f ( en N).
0,31 - 1,25 x 4,2 10-3 x 10 =0,31 -0,0525 ~0,26 N.
A - 25,9 10-2 Vrai.  B. 25,9 10-3. C. 25,9 10-4  D. 25,9 10-5. E. autre valeur.

7.  Quelle est en m / s la vitesse de la bille tombant dans la glyc�rine ?
Dur�e entre  deux images successives : 1 / 25 s ; distance parcourue par la bille : 0,05 m ; vitesse : 0,05 x25 ~1,25 m /s.
A - 0,05  B. 0,25. C. 1,25 Vrai.   D. 2,5. E. 5.

On r�alise une s�rie de mesures de vitesses avec des billes de rayons diff�rents et compos�es d'alliages de masses volumiques diff�rentes. Lorsque la vitesse  devient constante, les distances ( en cm) entre 2 images sont les suivantes :
Rayon de la bille ( cm)
 0,2
 0,5
 1
 2
 3
Masse volumique  7,5 g cm-3
 0,2
 1,25
 5
 20
 45
Masse volumique  5 g cm-3 0,12
 0,75
 3
 12
 27
Masse volumique  3,75 g cm-3 0,08
 0,5
 2
 8
 18

8. Quelle est la proposition exacte ?
A l'�quilibre, la vitesse  est :
Vlimite = (racier - r glyc�rine) 4 / 3 p R3 g / (6 p R h) = (racier - r glyc�rine) 4 / 3  R2 g / (6   h).
A - proportionnelle au rayon de la bille.
B - inversement proportionnelle au rayon de la bille.
C - proportionnelle � la surface de la bille.
D - inversement proportionnelle � la surface de la bille.
E - Proportionnelle au volume de la bille. Vrai.

 9. Quelle est la proposition exacte ?
A l'�quilibre, la vitesse  est :
Vlimite = (racier - r glyc�rine) 4 / 3 p R3 g / (6 p R h) = (racier - r glyc�rine) 4 / 3  R2 g / (6   h).
A - proportionnelle � la masse volumique de la bille.
B. inversement proportionnelle � la masse volumique de la bille.
C -  proportionnelle � la somme des masses volumiques de la bille et de la glyc�rine.
D - inversement proportionnelle � la somme des masses volumiques de la bille et de la glyc�rine.
D - inversement proportionnelle � la surface de la bille.
E - Proportionnelle � la diff�rence des masses volumiques de la bille et de la glyc�rine. Vrai.

10. On fait tomber la bille d'acier d'un cm de rayon dans un fluide de m�me masse volumique que la glyc�rine mais de viscosit� �gale � 0,11 Pa s. A l'�quilibre la vitesse de chute dans le fluide est �gale � 12,5 m /s. Quelle est en PI (1 PI = 1 Pa s), la viscosit� de la glyc�rine ?
La vitesse limite est inversement proportionnelle � la viscosit� du liquide.
1,25  h glyc�rine = 12,5 x 0,11 ; h glyc�rine =1,1 Pa s.
A. 0,02 ; B . 0,08 ; C. 0,23 , D. 0,70 ; E. 1,10. Vrai.

11. Quelle formule peut correspondre � l'expression de la force f ?
R�ponse B f = 6 p R h v.



Radioactivit�.
Le calcium 4720Ca est radioactif b�ta moins. Il donne du scandium avec une p�riode radioactive T1 = 4,54 jours. Cette transformation s'accompagne d'�mission de photons de 1,30 MeV. Le scandium fils est �galement radioactif avec une p�riode T2 = 3,35 jours et cette transformation s'accompagne de l'�mission de photons de 0,16 MeV. L'�l�ment fils est le titane, stable qui a le m�me nombre de masse que le scandium.
12. Quels sont les nombres de masse A et de charge Z du scandium fils ?
4720Ca ---> 4721Sc + 0-1e.
A. Z = 21 ; A = 48 ; B . Z = 20 ; A = 48 ; C. Z = 22 ; A = 47 , D. Z = 21 ; A = 47 Vrai ; E. Z = 20 ; A = 47.

13. Quel est le type de d�sint�gration du scandium, fils du calcium 47 ?
4721Sc ---> 4722Ti + 0-1e.
A - alpha ; B - b�ta moins. Vrai. C - b�ta plus  D - capture �lectronique. E - gamma.

14. Quels sont les nombres de masse A et de charge Z du titane ?
A. Z = 21 ; A = 48 ; B . Z = 20 ; A = 48 ; C. Z = 22 ; A = 47 Vrai, D. Z = 21 ; A = 47  ; E. Z = 20 ; A = 47.
.
15 Quelle affirmation est vraie ?:
A - Ces trois �l�ments ( calcium, scandium, titane ) diff�rent par leurs masses.
B - Ces trois �l�ments diff�rent par leur nombre de nucl�ons.
C - Ces trois �l�ments diff�rent par leur nombre de protons. Vrai.
D - Ces trois �l�ments ne diff�rent que par leur nombre de neutrons
E - Aucune des propositions ci-dessus.

16. Quelle est approximativement en s-1 la valeur de la constante de d�sint�gration du calcium 47 ?
l =ln2 / (4,54 x24 x3600) ~1,77 10-6 s-1. R�ponse B

17 - On dispose � t =0 d'une source de 350 MBq de calcium 47. A quel nombre d'atomes correspond cette activit� ?
N = A / l = 350 106 /(1,77 10-6) ~2 1014. R�ponse A

 18. A quelle masse ( en g ) correspond cette activit� ?
2 1014 / (6 1023 )~3,3 10-10 mol.
3,3 10-10 x 47 ~1,54 10-8 g. R�ponse E

19 - Quelle sera l'activit� du calcium 47 au bout de 9 jours ?
A = 350 exp(-9 ln (2) / 4,54) =88,6 MBq
ou bien 9 jours ~ 2 T1 ; 350 / 22 ~87,5 MBq. R�ponse C.
.
.


Initialement la source ne contenanit que du calcium 47 mais en se d�sint�grant, il y a formation de scandium radioactif. Celui-ci est cr�� progressivement et se d�sint�gre en partie. On mesure le rapport activit� de scandium / activit� du calcium sur 20 jours.


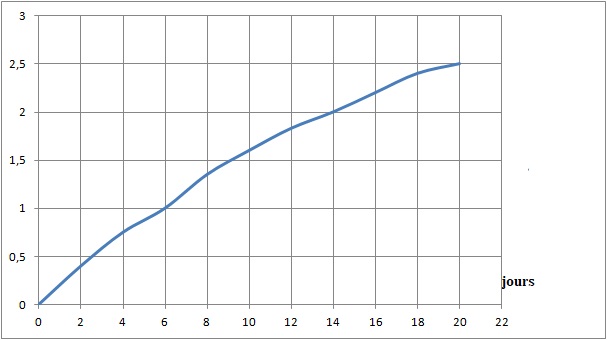
20. Qelle est approximativement, en MBq, l'activit� du scandium � t = 9 jours ?
Activit� du scandium / activit� du calcium =ASc / ACa = 1,5.
ACa = 350 exp (-ln(2) x9 / 4,54) =88,57 MBq.
ASc = 1,5 x88,57 ~133 MBq. R�ponse B.

21 - Au bout de combien de jours, les activit�s de calcium 47 et de son fils sont-lles �gales ?
ASc / ACa = 1 ; le graphe indique t ~ 6 jours. R�ponse B.

 22- Quelle est l'activit� totale mesur�e 100 heures apr�s le moment initial ?
100 h = 100 / 24 = 4,2 jours.
Activit� du scandium / activit� du calcium =ASc / ACa = 0,8.
ACa = 350 exp (-ln(2) x4,2 / 4,54) =184 MBq.
ASc = 0,8 x184 ~147 MBq.
Activit� totale : 184 +147 ~331 MBq.  R�ponse B.



23. Afin de rechercher une �ventuelle asymptote, les mesures sont poursuivie sur une dur�e de 100 jours.

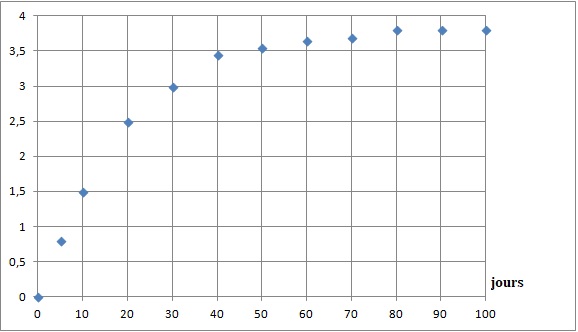
Quelle �quation semble mieux tenir compte des �v�nements constat�s ? ( " a" est une valeur num�rique)
Activit� du scandium / activit� du calcium 47 = 3,82(1-e-at). R�ponse C

24 - A quelle formule peut correspondre la valeur 3,82 mesur�e sur la courbe ?
T1 / (T1-T2) = 4,54/(4,54 -3,35)~3,82.  R�ponse E.

25 - Quelle est l'affirmation exacte ?
A - L'activit� du scandium va toujours augmenter au cours du temps.
B. Il faut plus d'une semaine pour que l'activit� du scandium d�passe celle du calcium. Vrai.
C. L'activy� du tiyane, va augmenter puis d�cro�tre au cours du temps. Faux ( le titane n'est pas radioactif ).
D - Apr�s un certain temps, l'activit� du scandium va �tre en �quilibre avec celle du calcium, c'est � dire en rapport constant. Vrai..
E - L'activit� gmobale des �l�ments issus du calcium ne va jamais devenir n�gligeable. Faux.

26. Quelle affirmation est inexacte ?
A. Il pourra y avoir � un moment donn� autant d'atomes de calcium que de scandium.
B. Il pourra y avoir � un moment donn� autant d'atomes de calcium que de titane.
C. Il pourra y avoir � un moment donn� autant d'atomes de scandium que de titane.
D. Il y aura � un moment donn� autant d'atomes de scandium qu'il y avait initialement d'atomes de calcium. Faux.
E. Il y aura � un moment donn� autant d'atomes de titane qu'il y avait initialement d'atomes de calcium.

L'�quation obtenue est modifi�e afin de permettre le calcul de a. On obtient la courbe suivante y = e-at.


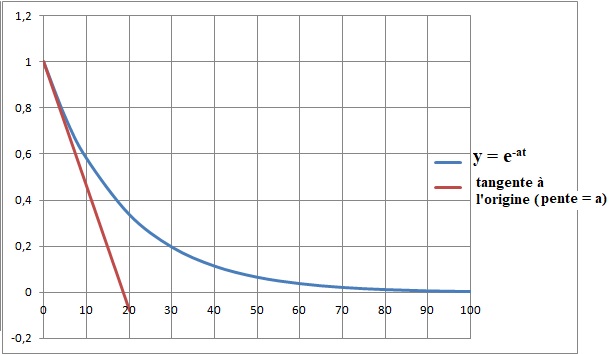
27 - Quelle est la valeur de a en j-1 ?
a = 0,054 j-1. R�ponse D.


28. Ces activit�s ont �t� mesur�es avec un appareil d�tectant les photons. Quelle est en �J, l'�nergie d�tect�e par l'appareil en une minute, s'il re�oit par seconde 106 photons �mis lors de la d�sint�gration du calcium 47 et n'en d�tecte que 5 % ?
Nombre de photons re�us par l'appareil en une minute 6 107.
Nombre de photons d�tect�s : 0,05 x 6 107 =3 106.
Energie : 3 106 x1,30 106 =3,9 1012 eV ou 3,9 1012 x1,6 10-19 =6,24 10-7 J = 0,624 �J. R�ponse C.

29 - Quelle est en nanom�tre la longueur d'onde des photons �mis lors de la d�sint�gration du scandium ?
E = h c / l avec E = 0,16 x1,6 10-13 =2,56 10-14 J.
l = 6,63 10-34 x 3 108 /(2,56 10-14) =7,77 10-12 m =7,77 10-3 nm. R�ponse D.

Optique.
Soient deux fentes fines parall�les distantes de a = 2,0 mm, dans l'exp�rience des fentes d'Young. On �claire ces fentes par une fente lumineuse parall�le aux pr�c�dentes et � �gales distance de chacune d'elles. On travaille dans l'air et on utilise une lumi�re monochromatique de longueur d'onde l. On observe des franges d'interf�rences sur un �cran P, parall�le au plan des fentes et situ� � D = 1 m du plan des fentes. La largeur de 14 interfranges cons�cutifs  est de 4,0 mm.

30. Quel ph�nom�ne intervient dans l'exp�rience des fentes d'Young ?
Diffusion ; att�nuation ; diffraction ; r�fraction ; r�flexion.

31. Quelle est en nm la longueur d'onde de la lumi�re utilis�e ?
i = lD /a avec i = 4,0 10-3 / 14 =2,857 10-4 m.
l = 2,857 10-4 x 2,0 10-3 / 1 =5,71 10-7 m = 571 nm. R�ponse A.

32. Sachant que la vitesse de la lumi�re dans un milieu est inversement proportionnel � l'indice de r�fraction de ce milieu, quelle affirmation serait fausse, si tout le dispositif �tait plong� dans un milieu d'indice diff�rent de celui de l'air ?
A. La vitesse de propagation du rayonnement lumineux serait diff�rente.
B. La longueur d'onde du rayonnement lumineux serait diff�rente.
C. La fr�quence du rayonnement lumineux serait diff�rente. Faux.
D. La distance entre deux interfranges serait diff�rente.
E. Le temps mis par le rayonnement lumineux pour se propager des fentes au plan serait diff�rent.

33. La source �met maintenant dans l'air deux radiations de longueurs d'onde �gales � 550 nm et 600 nm. On observe simultan�ment les deux syst�mes de franges. Quelle est en mm, par rapport � la position de la frange centrale, la plus petite distance o� les milieux des franges brillantes correspondant aux deux radiations co�ncident ?
i1 = 550 10-9 x1 / (2,0 10-3) =2,75 10-4 m = 0,275 mm = 275 �m
i2 = 600 10-9 x1 / (2,0 10-3) =3,0 10-4 m = 0,30 mm = 300 �m.
Plus petit multiple commun � 275 et 300 : 25 x11 x12 = 3300.
275 x12 = 3300 �m = 3,3 mm. R�ponse D.

34. A quelle nombre d'interfranges du rayonnement de 600 nm de longueur d'onde correspond cette superposition des deux franges ?
11. R�ponse D.



Dipole RLC.
On r�alise le montage suivant :


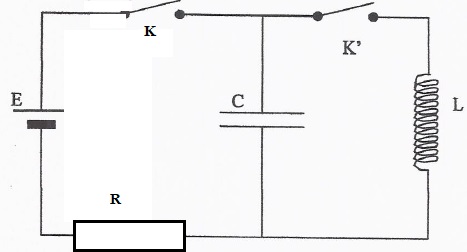
L = 10 mH ; C = 100 nF ; R = 100 ohms ; E =10 V. La r�sistance de la bobine est n�gligeable.
35. K est ferm� ; K' est ouvert. Le r�gime permanent est �tabli. Quelle est en A l'intensit� du courant qui travers la r�sistance R.
Le condensateur charg� se comporte comme un interrupteur ouvert : I = 0. R�ponse A.

36. Quelle est alors en �C la charge du condensateur ?
Q = C E = 10-7 x10 = 10-6 C =  1 �C. R�ponse B.

37. Quel est en ms la valeur de la constante de charge t du condensateur ?
t = RC = 10-7 x100 = 10-5 s =  0,01 ms.. R�ponse B.

38 -Le condensateur �tant d�charg�, on ferme K et K'. Le r�gime permanent �tant �tabli, quelle est en A l'intensit� du courant qui traverse la bobine ?
La bobine emmagasine de l'�nergie puis se comporte, en r�gime permanent,  comme un interrupteur ferm�.
La tension aux bornes de la bobine est nulle.
I = E / R = 10 /  100 = 0,1 A. R�ponse C.

39. Quelle est alors en �C la charge du condensateur ?
La tension aux bornes de la bobine �tant nulle en r�gime permanent, la tesnion aux bornes du condensateur est nulle.
Q = 0 �C. R�ponse A.

  40. Quelle est alors en �J l'�nergie emmagasin�e par la bobine ?
�L I2 =0,5 x 0,01 x 0,12 = 5 10-5 J = 50 �J. R�ponse C.

41 Que se passe t-il � l'ouverture de K ?
A - Rien. 
B - D�charge du condensateur.
C - Charge du condensateur.
D - Passage d'un courant suppl�mentaire dans le circuit contenant la r�sistance R.
E - apparition d'oscillations libres dans le circuit constitu� par la bobine et le condensateur. Vrai.

Niveau d'�nergie de l'atome de sodium.
E0 = -5,14 eV ; E2 = -1,94 eV ; E3 = -1,52 eV ; E5 = -0,85 eV.
42. Lors du passage de l'�tat excit� d'�nergie E4 � l'�tat fondamental il y a �mission d'un photon de longueur d'onde 330 nm.
 A quel domaine spectral appartient ce photon ?
UV. R�ponse D.

43. Quel est en eV, la valeur de l'�nergie du niveau E4 ?
DE = E4-E0 = h c / l = 6,63 10-34 x3 108 / (330 10-9) =6,03 10-19 J ou 3,77 eV.
E4 = -5,14 +3,77= -1,37 eV. R�ponse E.

44- Lors du passage de l'�tat excit� d'�nergie E2 � l'�tat excit� E1, il ya �mmission d'un photon de longueur d'onde 1138 nm. Quel est en eV la valeur du niveau d'�nergie E1 ?
DE = E2-E1 = h c / l = 6,63 10-34 x3 108 / (1138 10-9) =1,75 10-19 J ou 1,09 eV.
E1 = -1,94 -1,09= -3,03 eV. R�ponse B.
.
45 -  L'atome de sodium pris dans son �tat fondamental absorbe un photon de longueur d'onde 589,3 nm. Quel est alors le niveau d'�nergie de l'atome de sodium ?
h c / l = 6,63 10-34 x 3 108 /(589,3 10-9) =3,375 10-19 J ou 2,11 eV.
-5,14 +2,11 = -3,03 eV ( niveau excit� E1 ). R�ponse  A.


  

menu