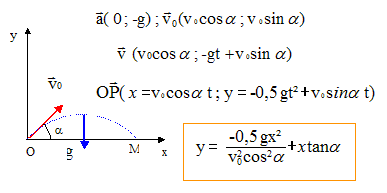Distance
terre lune, rotation d'une fronde,
Concours audioprothésiste Paris 2019.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
......
.....
|
|
|
Détermination approchée de la distance terre-lune.
I. On suppose que la terre de centre O, de masse MT a une distribution de masse à symétrie sphérique. On considère la lune comme un point matériel de masse ML.
Dans le référentiel géocentrique, la lune n'est soumise, en première
approximation, qu'à la force de gravitation terrestre et décrit une
trajectoire circulaire de centre O. Soit d la distance de la terre au
centre de la lune.
1. Montrer que le mouvement circulaire de la lune est uniforme.
La
lune est soumise uniquement à la force de gravitation de la terre,
force centripète, perpendiculaire à chaque instant à la vitesse.
Par conséquent cette force ne travaille pas et ne modifie pas l'énergie cinétique de la lune.
La valeur de la vitesse de la lune est donc constante : le mouvement est uniforme..
2. Exprimer la vitesse v de la lune en gonction de G, MT et d.
F = G ML MT / d2 = ML a =ML v2 / d.
v2 =G MT / d ; v = [G MT / d]½.
3. En déduire la période TL de révolution de la lune en fonction de G, MT et d.
La lune décrit la circonférence 2 p d à la vitesse v en TL seconde.
2 p d = v TL ; 4 p2 d2 = v2 TL2.
4 p2 d2 = G MT / d TL2.
4 p2 d3 = G MT TL2.
TL = [4 p2 d3 /( G MT)]½.
4. Enoncer la troisième loi de Kepler et montrer qu'elle est vérifiée.
Le carré de la période de révolution est proportionnelle au cube du rayon de l'orbite.
TL2= 4 p2 / (GMT) d3 .
5. Exprimer la constante présente dans cette loi en fonction des grandeurs données.
4 p2 / (GMT) = constante.
6. Calculer la valeur numérique de cette constante.
4 x3,142 / (6,67 10-11 x6,0 1024) =9,86 10-14 s2 m-3.
7. Schant que TL = 27 j 7 h 30 min, en déduire une valeur approchée de la distance du centre de la terre au centre de la lune.
TL = 27 x24 x3600 +7 x3600 +30 x60 =2 359 800 s.
d3 =2 359 8002 / 9,86 10-14 =5,65 1025.
d=3,8 108 m = 3,8 105 km.
II. On se propose de déterminer la distance terre au centre de la lune à l'aide d'un laser.
Un rayon laser émis depuis la terre se propage jusqu'à la lune, pour y
être rfléchi par un miroir vers la station émettrice terrestre.
1. Sachant que la durée qui s'écoule entre l'émission et la réception du faisceau est Dt = 2,563 s, en déduire une valeur approchée de la distance du centre de la terre au centre de la lune.
Distance terre lune = 3,0 108 x 2,563 / 2 = 3,84 108 m = 3,84 105 km.
Distance des centres des deux astres :
3,84 105 + Rterre + Rlune = 3,84 105 +6380+1378=3,9 105 km.
2. Ce résultat est-il en accord avec celui de la question 7 ?
Ecart relatif : ( 3,9 -3,8 )/3,8 = 2,6 10-2 ( 2,6 %).
Les résultats sont en accord.
|
|
|
III La télémétrie laser plus en détail.
On utilise un laser de longueur d'onde l =
476 nm qui délivre des impulsions de 15 kJ de durée 50 ns. Un
réflecteur de diamètre 2,0 m est situé sur la lune et on le considèrera
perpendiculaire au faisceau laser. :
1. Evaluer l'ordre de grandeur du nombre de photons émis lors de chaque impulsion.
Energie du faisceau : 15 103 J.
Energie d'un photon : h c / l =6,63 10-34 x 3,0 108 / (476 10-9) =4,18 10-19 J.
Nombre de photons émis : 15 103 / (4,18 10-19) ~3,6 1022.
2. Calculer la puissance instantanée du faisceau.
15 000 / (50 10-9) =3,0 1011 W.
3.
La divergence du faisceau crée un cône de demi angle q = l /a où a est le diamètre de sortie du faisceau ( a = 3,0 mm). Déterminer le diamètre de la tache au niveau du miroir.
q = 476 10-9 / (3,0 10-3) =1,59 10-4 radian.
Diamètre de la tache sur la lune : 1,59 10-4 x 3,84 108 =6,1 104 m.
4. En déduire la puissance réémise par le réflecteur, en supposant que le réflecteur est parfaitement réfléchissant.
Surface du réflecteur : pR2 = 3,14 m2.
Surface de la tache sur la lune : 3,14 x (6,1 104)2 / 4 =2,9 109 m2.
Puissance réémise : 3,0 1011 x3,14 / (2,9 109) =3,2 102 W.
5.
La lumière réfléchie est recueillie par un télescope de diamètre
2,0 m. Le faisceau réfléchi fait un cône de demi-angle au sommet a = 4,0 10-7 rad.
Déterminer la puissance reçue par le télescope.
Rayon de la tache sur la terre : 4 10-7 x3,84 108 =153,6 m.
Surface de cette tache : 3,14 x153,62 =7,4 104 m2.
Surface du télescope : 3,14 x22 /4=3,14 m2.
Puissance recue par le télescope : 3,2 102 x3,14 / (7,4 104) =1,36 10-2 W.
6. Evaluer l'ordre
de grandeur du nombre de photons reçus par impulsion par le télescope.
Ciomparer au nombre de photons de départ.
Energie reçue : 1,36 10-2 x50 10-9 =6,8 10-10 J.
Nombre de photons reçus : 6,8 10-10 /(4,18 10-19) =1,6 109.
1,6 109 / (3,6 1022) ~4,5 10-14.
7. Quelles propriétés du laser ont été mises à profit ?
Faisceau très directif ; puissance élevée par unité de surface.
|
|
|
...
|
|
.
|
....
|
Rotation d'une fronde.
Un caillou de masse m = 250 g, supposé ponctuel, est accroché à
l'extrémité d'une fronde de longueur L = 1,00 m. On lui fait décrire un
cercle de centre O, immobile, à une vitesse constante de 4 tours
par seconde. La position du caillou est repérée par l'angle q que fait le fil avec l'horizontale ( q(t=0) = 0).
1. Calculer la vitesse angulaire de la fronde.
4 tours par seconde soit w =4 x2 x3,14 = 25,1 rad /s.
2. Calculer la vitesse du caillou.
v = w L = 25,1 m /s.
3.
Déterminer les caractéristiques du vecteur vitesse du caillou par
rapport à la terre à un instant t en coordonnées cartésiennes et dans
le repère de Frenet.
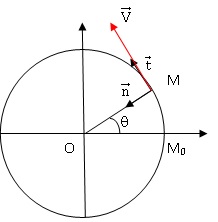
Coordonnées du point M : cos q ; sin q avec q = wt.
Coordonnées cartésiennes du vecteur vitesse :
Dérivée du vecteur position par rapport au temps : -w sin q ; w cos q.
Dans la base de Frenet, coordonnées du vecteur vitesse :
Le vecteur vitesse est à chaque instant tangent à la trajectoire ; suivant l'axe t : V ; suivant l'axe n : 0.
4. Déterminer dans les mêmes systèmes de coordonnées, les caractéristiques du vecteur accélération du caillou.
Dériver le vecteur vitesse par rapport au temps :
en coordonnées cartésiennes : -w2 cos q ; - w2 sin q.
Dans la base de Frenet, accélération centripète :
suivant l'axe n : an=V2 / OM = V2 ; suivant l'axe t : 0.
5. En déduire l'intensité de la force exercée par la fronde sur le caillou.
F =m an =mV2 =0,25 x25,12 =157,5 ~1,6 102 N.
On néglireant le poids du caillou, la poussée d'Archimède et les frottements.
Le caillou est alors lancé avec une vitesse de valeur v0. Le vecteur vitesse fait un angle a
avec l'horizontale. On néglige les frottements et la poussée
d'Archimède. Le point O de départ se situe au niveau du sol horizontal.
L'origine des temps est l'instant de départ du caillou.
6. Après avoir établi les équations horaires du mouvement, déterminer la distance maximale atteinte par le caillou en fonction de a.
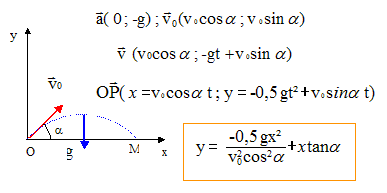
Au sol y = 0.
-0,5 g x /( v02 cos a) + sin a = 0.
x = 2 v02 cos a sin a / g = v02 sin (2a) / g.
7. Montrer qu'il
existe un angle de tir pour lequel cette distance est maximale, et
déterminer la valeur de cet angle. Calculer la distance maximale
atteinte.
La distance est maximale lorsque sin ( 2a) = 1 soit a = 45°.
xmax = v02 / g = 25,12 / 9,81 =64,2 m.
8. Pour cette valeur particulière de a, quelle est l'altitude maximale atteinte ?
A cette altitude la composante verticale de la vitesse est nulle.
t = v0 sin 45 / g =25,1 sin 45 / 9,81 =1,81 s.
ymax = -0,5 x9,81 x1,812 +25,1 sin 45 x1,81 ~ 16,1 m.
9. Quelle sera alors la vitesse du caillou ?
v0 cos 45 =25,1 cos 45 ~17,7 m /s.
10. Avec cette valeur particulière de a, le caillou atteindra-t-il le front d'un adversaire de grande taille ( entre 2,0 et 2,20 m) se trouvant à 62 m du lanceur ?
x = v0 cos a t ; t = 62 / (25,1 cos 45) =3,493 s.
y = -0,5 x9,81 x3,4932 +25,1 x sin 45 x3,493 = -59,86 +62,0 ~2,14 m.
Le front est atteint.
|
|