QCM
Physique, concours orthoptie Bordeaux 2019.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
Mécanique.
Question 21
Sur le chemin en terre du jardin, la tortue
Josie, à l'arrêt sur le porche de sa maison, observe les
alentours et aperçoit au loin sa copine tortue Lucette. Elle démarre en
trombe juste à la sortie de sa maison avec une accélération a = 200 µm
/s2 ; 4,00 m plus loin, elle arrive au niveau de Lucette à 12 h 50 min 04 s.
A quelle heuure Josie est-elle sortie de sa maison ?
x = ½at2 ; t = (2x / a)½ = (2 x4,00 / (200 10-6))½ ~119=200 s= 3 min 20 s
Heure de départ : 12 h 46 min 44 s
Réponse D.
Question 22. (suite)
A l'instant où Josie arrive au niveau de Lucette, quelle est sa vitesse ?
v = at = 200 10-6 x200 = 0,04 m /s = 40 mm / s.
Réponse B.
Question 23.( suite).
Arrivée
au niveau de Lucette, Josir se rend compte qu'elle a oublié son
rendez-vous avec Jack le crapaud à 13 h. Elle poursuit donc sa route à
vitesse constante sans changer de direction. Lucette, vexée que Josie
ne s'arrête pas, démarre aussitôt que Josie la dépasse et maintient une
accélération de 250 µm / s2. Au bout de combien de temps ( à partir de l'instant du dépassement ) Lucette rattrapera t-elle Josie ?
Josie : x = vt = 0,04 t.
Lucette : x = ½at2 = 1,25 10-4 t2.
1,25 10-4 t2 = 0,04 t ; t = 0 ( départ) ; t = 320 s.
Réponse E.
Question 24. suite
A l'instant où Lucette ratrappe Josie, quelle est la vitesse de Lucette ?
v = at = 2,5 10-4 x320 =0,08 m /s = 80 mm / s.
Réponse A.
Question 25 ( suite)
A quelle distance de la maison de Josie, Lucette rattrape -t-elle Josie ?
Distance parcourue par Lucette : 1,25 10-4 x3202 =12,8 m.
ou 320 x0,04=12,8 m.
Distance parcourue par Josie : 1,0 10-4 x2002 =4 m.
Total 12,8 +4 = 16,8 m.
Réponse C.
|
|
|
Acoustique.
Question 26
Lorsque deux sons différents nous parviennent en
même temps aux oreilles, ce sont les intensités sonores qui s'ajoutent.
Un ensemble vocal dispose de 5 chanteurs. Si on souhaite augmenter le
niveau sonore de 13 dB, combien de chanteurs devront nous à peu
près rajouter ?
Intensité sonore d'un chanteur : I ; nombre de chanteur ajouté : n.
Itotal =(n+5) I = I0 100,1 L +1,3 ; I initial = 5 I = I0 100,1 L ;
(n+5) /5 =101,3~ 20 ; n =95.
Réponse D.
Question 27
L'intensité sonore en champ libre décroît en 1 / r2
( où r désigne la distance par rapport à la source ). Un chanteurr seul
produit un niveau sonore de 82 dB à 10 m. Combien de chanteurs de même
puissance sonore que le chanteur précédent faut-il pour produire le
même niveau sonore de 82 dB à 48 m ?
Chanteur seul à 10 m : intensité sonore I /102 = k avec k une constante.
n chanteurs à 48 m : intensité sonore n I / 482 = k = I / 100 ; n = 482 /100.
n = 23.
Réponse B.
.
Question 28.
Une
chorale composée de 12 chanteurs de même puissance produit un niveau
sonore de 81 dB à 15 m. A quelle distance devrions nous nous placer
pour obtenir le même niveau sonore dans le cas de 3 chanteurs (
toujours de même puissance ) ?
12 chanteurs à 15 m : intensité 12 I /152 = k avec k une constante.
3 chanteurs à la distance d : intensité sonore 3 I / d2 = k =1220 I /152 ; d = (3 / 12)½ x15 ~7,5 m.
Réponse D.
|
|
|
|
Divers.
Question 29
Considérons une vitesse v, une masse M et une longueur L. Les unités va Mb Lg sont celles d'une pression pour :
Pression = force / surface = masse fois accélération / longueur2 soit M L T -2 / L2 = M L2 T -2 / L3 = M v2 L-3.
a = 2 ; b = 1 ; g = -3.
Réponse C.
.Question 30.
En électronique, la pente des courbes est exprimée enn dB /
décade où une décade représente une multiplication par 10 de la
fréquennce.
En acoustique, la pente des courbes est exprimée en dB / octave
où une octave représente une multiplication par 2 de la fréquence.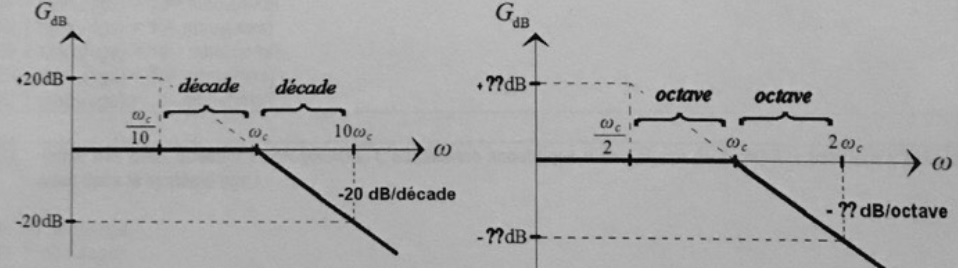
Une pente de -20 dB/décade est équivalente à une pente de :
-20 x log 10 = -20 dB / décade ; -20 x log2 = -6 dB / octave.
Réponse B.
|
|
|