QCM Mathématiques concours Audioprothésiste Bordeaux 2019.

QCM Mathématiques, concours Audioprothésiste Bordeaux 2019.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

.
.

Exercice 1. Question 1
n désigne un entier natuerl et x un réel non nul.
xⁿ⁺⁵ / (xⁿ)⁵ est égal à :
A - 1.
xⁿ⁺⁵ / x⁵ⁿ =x⁵ / x⁴ⁿ.
B - 1 / x⁴ⁿ.
C . x⁵ / x⁴ⁿ. Vrai.
D - x⁴ⁿ⁺⁵.
E - aucune des réponses proposées.
Question 2
x⁵ x²ⁿ / (x⁵ⁿ x²) est égal à :
A. 1 /x³.
x^5+2n-5n-2=x^3-3n.
B . 1/ x³ⁿ.
C . 1.
D . x^3-3n. Vrai.
E . aucune des solutions proposées..
Question 3
(2⁸ +8^-4)^½ / (2²+8^-6)^½ est égal à :
A . (2⁴ +8^-2) / (2 +8^-3) .
(2⁸ +1/2¹²)^½ / (2²+1/2¹⁸)^½ ; réduire au même dénominateur et simplifier.(2¹⁸ / 2¹²)^½ =2³=8.
B 10³ / 10².
C .(2⁶ +8²)^½.
D . 8. Vrai
E . aucune des solutions proposées. ..

Question 4
Pour x >0, l'expression e^-ln(x) est égale à :
A -e^x.
1/e^ln(x) = 1 / x.
B . 1/e^x.
C -x
D . e^-x.
E . 1/x. Vrai.
Question 5
Pour x >0, l'expression e^2+ln(x) est égale à :
A.e^2x..
e² * e^lnx = x e².
B . x e². Vrai.
C . x².
D .2e^x.
E 1/e^x.
Question 6
(e^x+1) / (e^-x+1) est égale à ::
A.1
(e^x+1) / (1/e^x+1) =(e^x+1) / [ (e^x+1) / e^x] =e^x.
B . e^x. Vrai.
C . e^2x+1.
D .1/e^x.
E aucune des solutions proposées.

Exercice 2. x est un réel.
Question 7
La dérivée de (e^x+2) /(e^x+3) est égale à ::
A. 0.
On pose u = e^x+2 et v = e^x+3 ; u' = v' = e^x.
(u'v - v'u / v² = e^x /(e^x+3)².
B . 2/3..
C . e^x /(e^x+3)². Vrai.
D .1 /(e^x+3)².
E (2e^2x +5e^x) /(e^x+3)².

Exercice 3 . x est un réel strictement positif.
Question 8
La dérivée de ln(1/x) est égale à :
A. -1 /x. Vrai.
On pose u = 1 /x ; u' = -1/x². u' / u = -1 /x.
B . 1/x³.
C . 1/x.
D .ln(x) / x..
E aucune des solutions proposées.
.Question 9
La dérivée de 1/x^½ est égale à :
A. 1 /(2x^3/2)
(x-½)' = -0,5 x^-3/2.
B . -x / x^½.
C . 2x^½.
D . -1 /(2x^3/2). Vrai.
E 1 /(2x^½).
Question 10
La dérivée de (ln(x) )² est égale à :
A. 2 ln(x) / x. Vrai.
On pose u = ln(x) ; u' =1/x : 2uu' = 2ln(x) / x.
B . 2x ln(x)
C . 1/x.2x (ln(x))².
D .2 ln(x).
E ln(x).

Exercice 4. x est un réel strictement positif.
Question 11
une primitive de ln(x) / x est égale à :
A . 1 /(2x)
On pose u = ln(x) ; u' = 1 /x.Une primitive de u u' est 0,5 u² soit 0,5( ln(x))²..
B 1 /x².
C ( ln(x))².
D . 0,5( ln(x))². Vrai.
E .aucune des solutions proposées.
Question 12
Une primitive de x⁴+7 est égale à :
A 4x³+7x
x⁵ / 5 +7x + constante.
B x⁵/5 +7x +4. Vrai.
C x⁴/4 +7x.
D x⁵ +7x.
E . aucune des réponses proposées..
.
Exercice 5.
Question 13
La valeur de l'intégrale suivante est égale à :

Réponse E.

Question 14
La valeur de l'intégrale suivante est égale à :

Réponse E.

Question 15
La valeur de l'intégrale suivante est égale à :

Réponse A.
Question 16.
Une primitive de la fonction (2x+3)² est :
A . (2x+3)³ / 6. Vrai.
On pose u = 2x+3 ; u' = 2 ; primitive de u² : u³ / (3u') =(2x+3)³ / 6.
B -   (2x+3)³ / 3.
C   (2x+3)³ .
Question 16.
Une primitive de la fonction (2x+3)² est :
A . (2x+3)³ / 6. Vrai.
On pose u = 2x+3 ; u' = 2 ; primitive de u² : u³ / (3u') =(2x+3)³ / 6.
B -   (2x+3)³ / 3.
C   (2x+3)³ .
D 2(2x+3)³ .
E 6(2x+3)³ .

Exercice 6.
Soit la fonction f(x) = (5x³ -4x² -5x +5) / (x²-1).

Question 17.
L'ensemble de définition de f est :
A . ([1 ; + oo[.
Le dénominateur ne doit pas être nul, donc x différent de -1 et de 1.
B . ]-oo ; 1 [ union ]1 ; 1 [ union ]1 ; +oo[. Vrai.
C   ]-oo ; -1 [ union ]1 ; +oo[
D ]1 ; +oo[.
E aucune des réponses proposées.

Question 18.
La limite de f(x) en plus l'infini est égale à ::
A . plus l'infini. Vrai.
B    moins l'infini.
C 5
D -5
E zéro
Question 19.
La limite de f(x) en moins l'infini est égale à ::
A . plus l'infini.
B    moins l'infini. Vrai.
C 5
D -5
E zéro
Question 20.
La limite de f(x) en zéro est égale à :
A . plus l'infini.
B    moins l'infini.
C 5
D -5. Vrai.
E zéro
Question 21.
La limite de f(x) en -1⁺ est égale à ::
A . plus l'infini. Vrai.
B    moins l'infini.
C 5
D -5
E zéro
Question 22.
La limite de f(x) en -1^- est égale à ::
A . plus l'infini.
B    moins l'infini. Vrai.
C 5
D -5
E zéro
Question 23.
La limite de f(x) en 1⁺ est égale à ::
A . plus l'infini. Vrai.
B    moins l'infini.
C 5
D -5
E zéro
Question 24.
La limite de f(x) en 1^- est égale à ::
A . plus l'infini.
B    moins l'infini. Vrai.
C 5
D -5
E zéro

Question 25
La fonction f(x) :
A . admet une asymptote horizontale d'équation x =1.
B . admet une asymptote verticale d'équation y = 1.
C . admet une asymptote verticale d'équation x = 1. Vrai
D . admet une asymptote horizontale d'équation y = 1.
E . aucune des solutions proposées.

Question 26
La fonction f(x) :
A . admet une asymptote oblique d'équation y = 5x-4. Vrai.
B . admet une asymptote oblique d'équation y = 4-5x.
C . admet une asymptote oblique d'équation y = x- 1.
D . admet une asymptote oblique d'équation y = x+1.
E . n'admet pas d'asymptote oblique.

Exercice 7.
Soit la fonction g(x) = ln(e^x/x) = ln(e^x) - ln(x) = x-ln(x).

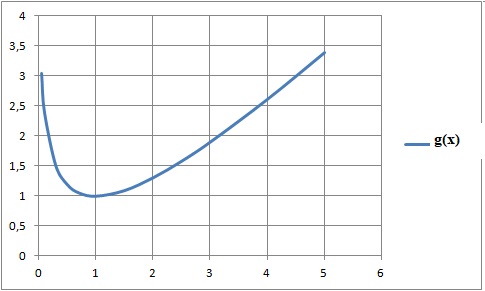
Question 27.
L'ensemble de définition de g est :
A [0 ; +oo[
L'ensemble de définition est ]0 ; + oo[
B ]-oo ; 0 [ union ]0 ; +oo[
C [1 ; +oo[
D ]1 ; +oo[
E aucune des solutions proposées.Vrai.

Question 28
La limite en O⁺ de g est égale à :
.A . plus l'infini. Vrai.
B.moins l'infini.
C. zéro.
D. 1
E. e.

Question 29
La limite en plus l'infini de g est égale à :
.A . plus l'infini. Vrai.
B.moins l'infini.
C. zéro.
D. 1
E. aucune des solutions proposées.

Question 30.
Sur son ensemble de définition la fonction g est :
A. strictement croissante.
g '(x) = 1-1 /x ; g '(x) est positive si x >1 et négative si x < 1.
sur ]0 ; 1 [ la fonction est décroissante puis croissante.
B. strictement décroissante.
C. monotone.
D. constante.
E. aucune des solutions proposées. Vrai.

Question 31.
Sur [1 ; +oo[ la fonction g est :
A. strictement croissante. Vrai.
B. strictement décroissante.
C. monotone.
D. constante.
E. aucune des solutions proposées.

Question 32.
Sur ]0 ; 1]la fonction g est :
A. strictement croissante
B. strictement décroissante. Vrai.
C. monotone.
D. constante.
E. aucune des solutions proposées.

Question 33.
Sur son ensemble de définition, l'équation g(x) =0 admet exactement :
A. aucune solution. Vrai.
B. une solution
C exactement deux solutions distinctes.
D. exactement 3 solutions distinctes.
E. aucune des solutions proposées.

Question 34.
Sur son ensemble de définition, l'équation g(x) =1 admet exactement :
A. aucune solution.
B. une solution Vrai.
C exactement deux solutions distinctes.
D. exactement 3 solutions distinctes.
E. aucune des solutions proposées.

Exercice 8.
Dans le plan complexe, on considère les points : A d'affixe z_A = 3+i 3^½ ; B d'affixe z_B = 2+2i ; C d'affixe z_C = 1-i ; D d'affixe z_D = -1+i 3^½. E d'affixe z_E = -3 -3i.
Question 35
Le module du nombre complexe z_A vaut :
A. 3*3^½.
(3² +3)^½ =2 *3^½.
B. 3^½.
C. 3
D .2*3^½. Vrai.
E. 12.

Question 36
Une valeur de l'argument du nombre complex z_A est :
A. p /3.
z_A / |z_A| = 3^½ / 2+0,5 i = cos ( p/6) + i sin (p/6).
B . p/4
C . p/6. Vrai.
D. -p/3.
E -p/6.

Question 37
L'angle (OC,OA) vaut :
A. p /12.
Un argument de z_C est -p /4.
L'angle cherché vaut donc : p /4 + p /6 = 5p/12.
B . 5p /12.. Vrai.
C .-p /12..
D . -5p /12.
E. p /2..

Question 38
L'angle (OB,OC) vaut :
A. p /2.
Un argument de z_B est +p /4.
L'angle cherché vaut donc : -p /4 - p /4 =- p/2.
B . -p /4..
C .0.
D . p /4.
E. -p /2.Vrai.

Question 39
Le nombre complexe z_D / z_A est :
A. un imaginaire pur de la forme ib avec b srtictement positif..Vrai.
(-1+i 3^½) / (3 +i 3^½) = (-1+i 3^½) (3 -i 3^½) /12 = i 3^½/3.
B. un imaginaire pur de la forme ib avec strictement négatif..
C. Un nombre réel strictement po bsitif.
D. un nombre réel strictement négatif..
E. de la forme a +ib avec a et b réels tous deux non nuls.

.Question 40
Le nombre complexe z_B / z_E est :
(2+2i) / (-3-3i) = -(2+2i) (3-3i) / 18 = -2/3.
A. un imaginaire pur de la forme ib avec b srtictement positif..
B. un imaginaire pur de la forme ib avec strictement négatif..
C. Un nombre réel strictement positif.
D. un nombre réel strictement négatif. Vrai..
E. de la forme a +ib avec a et b réels tous deux non nuls.



menu