QCM
acoustique, concours Audioprothésiste Bordeaux 2019.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
Acoustique.
Question 1
Un
ensemble vocal dispose de trois chanteurs. Si on souhaite augmenter le
niveau sonore de 9 dB, combien de chanteurs devrions nous à peu près
rajouter ?
A - 12.
Les intensités sonores s'ajoutent.
Avec N chanteurs : L = 10 log(NI / I0)=10 log N + 10 log (I
/ I0) ;
avec N' chanteurs : L+9 = 10 log (N'I
/ I0)=10 log N' + 10 log ( I / I0)= L-10 log N+10
log N'.
9=10 log (N' / N) ; N' /N= 100,9 ~8.
N'=8N ; N'-N = 7 N avec N = 3 ; N' = 21.
B - 20.
C - 24
D - 21. Vrai.
E - 9.
Question 2
Vous
écoutez un concert en plein air à 100 m de la scène. Derrière vous se
trouve une paroi rocheuse. Sachant que si l'écho nous parvient au bout
de moins de 50 ms, nous ne sommes pas capables de le dissocier du son
direct, quelle doit être la distance maximale de la paroi par rapport à
vous pour ne pas être géné par l'écho ?
A. 8,5 m. Vrai.
Le son doit parourir l'aller + retour en moins de 0,05 s à la
célérité de 340 m /s ;
2 x < 340x0,05 ; x < 8,5 m..
B . 17 m
C . 12,5 m.
D . 85 m .
E . 170 m..
Question 3
L'intensité sonore en champ libre décroît en 1 / r2
( où r désigne la distance par rapport à la source ). Un chanteur
produit un niveau sonore de 88 dB à 12 m. Combien de chanteurs de même
puissance sonore faut-il pour produire le même niveau à 48 m.
A . 12 .
La distance est multipliée par 4 ; l'intensité sonore est donc divisée
par 16 ( pour un chanteur ).
Pour retrouver le même niveau sonore à 48 m, il faut 16 chanteurs.
B . 16. Vrai.
C .32.
D . 36.
E . 120.
Question 4
Une
chorale composée de 16 chanteurs de même puissance produit un niveau
sonore de 86 dB à 16 m. A quelle distance devrions-nous nous placer
pour obtenir le même niveau sonore dans le cas d'un chanteur seul ?
A . 6,4 m.
L'intensité sonore sera divisée par 16 ; la distance doit être divisée
par 4 soit 4 m
B . 2,0 m
C 4,0 m. Vrai.
D . 14 m
E . 5,2 m
Question 5
On
enregistre la note La3 ( 440 Hz) sur la piste d'une pellicule de
cinéma. Une copie vidéo de ce film est ensuite réalisée. Or la vitesse
de défilement est de 24 images par seconde pour le cinéma et de 25
images par seconde pour la vidéo, ce qui fait que lors de la diffusion,
la fréquence perçue ne sera pas la même, selon qu'on assiste à une
projection cinéma ou vidéo. Calculez la fréquence entendue lors d'une
projection vidéo.
A.439 Hz.
440 / 24 ~18,3 battements de la note La par image.
440 / 24 x 25 = 458,3 battements pour 25 images.
B . 415 Hz.
C . 422,4 Hz.
D .440 Hz.
E 458,3 Hz. Vrai.
|
|
|
Question 6
Pour
sonoriser un terrain de jeu, on dispose de 3 enceintes acoustique,
délivrant chacune une puissance acoustique de 100 mW. Lorsque ces
enceintes ne fonctionnent pas, on relève un bruit ambiant de 65 dB.
Quel niveau sonore prévoyez-vous pour une personne situé à 2 m de la
première enceinte, à 5 m de la seconde et à 10 m de la troisième ? :
A . 89,9 dB.
Intensité sonore due au bruit ambiant : 10-12 x106,5
=10-5,5 = 3,16 10-6 W m-2.
Intensité sonore due à la première enceinte : 0,100 / (4 x3,14 x22)=1,98
10-3 W m-2.
Pour la seconde : 0,100 / (4 x3,14 x52 )=3,18 10-4
W m-2 ; pour la troisième : 0,100 / (4 x3,14 x102
)= 7,96 10-5 W m-2.
Intensité sonore totale : 2,38 10-3 W m-2 ; L =
10 log(2,38 10-3 / 10-12) =93,7 dB.
B
90,2 dB
C 93,8 dB. Vrai.
D . 92,0 dB
E .87,7 dB
Question 7
Johny
et Sylvie chantent un duo et l'on mesure un niveau sonore de 92,0 dB.
sylvie s'arrète de chanter et l'on mesure un niveau de 90,0 dB.
Pouvez-vous en déduire le niveau sonore si Sylvie chantait seule ?
A 90,2 dB.
Intensité sonore due à Johny : I = 10-12 x 109 =
10-3 W m-2.
Intensité sonore due au deux chanteurs : 10-12 x 109,2
= 1,58510-3 W m-2.
Intensité sonore due à Sylvie : 5,8510-4
W m-2. Niveau sonore correspondant : 87,7 dB.
B 92,0 dB
C
87,7 dB. Vrai.
D 92,0 dB.
E . 89,9 dB.
.
Question 8
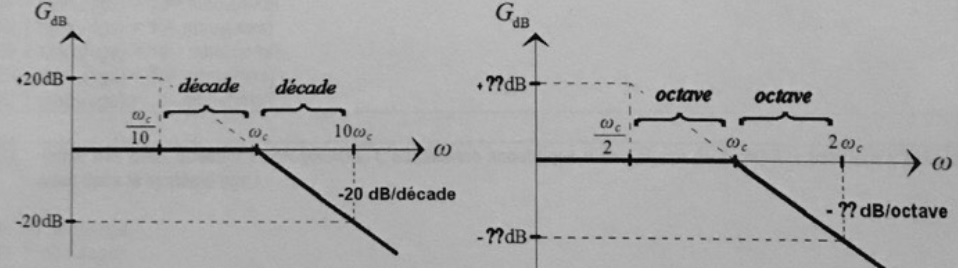
Une pente de -20 dB/décade est équivalente à une pente de :
-20 x log 10 = -20 dB / décade ; -20 x log2 = -6 dB / octave.
A -2 dB / octave.
B
- 6 dB / octave. Vrai.
C
-2,5 dB /octave
D - 4 dB/octave.
E - 10 dB / octave.
Question
9
L'admittance acoustique est donnée par Y = Vw /(rc2). V :
volume en m3 ; r
= 1,2 kg m-3, masse volumique de
l'air ; c = 340 m /s ; w
= 2 pf (rad /s) et f : fréquence en hertz.
Calculer Y pour f = 226 Hz et V = 1 mL.
A . 10-4
mho.
Y = 10-6 x226 x2x3,14 / (1,2 x3402)
=1,0 10-8 mho.
B . 1 µmho.
C . 10-8
mho. Vrai.
D . 1 mmho.
E . 10 cmmho.
Question 10
Concernant
l'admittance acoustique Y, les praticiens ont l'habitude de raisonner
dans le système cgs ( cm g s). Trouver l'équivalence entre les deux
systèmes.
A . 1 mho ( cgs) =
10-5 mho ( MKS).
Y(cgs) = 1 x2 x3,14 x226 /(1,2 10-3 x340002)=1,0
10-3 mho ( cgs).
B - 1
mho ( cgs) = 105 mho ( MKS). Vrai.
C 1
mho ( cgs) = 10-3 mho ( MKS).
D 1 mho ( cgs) = 103
mho ( MKS).
E 1 mho ( cgs) = 1 mho (
MKS).
|
|
|
|
Question 11
L'admittance acoustique d'un volume de 1 mL à la fréquence 226 Hz vaut
dans le système cgs :
A . 10 mho(cgs)
B . 1 mho (cgs).
C . 1 kmho(cgs).
D . 10 kmho( cgs).
E . 1 mmho (cgs). Vrai.
Question 12
Mesure du niveau sonore par bande d'octave. Concernant la répartition
par bande d'octave suivante, Lglobal est égal à :
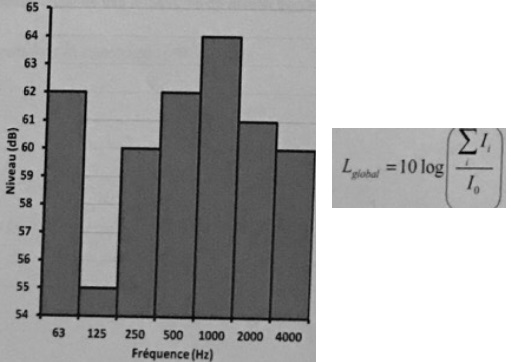
Itotal / I0
= 106,2 +105,5+106+106,2+106,4+106,1+106
=(1,585 +0,316+1+1,585+2,512+1,26 +1) 106=9,258 106.
L = 10 log(9,258 106) =69,7 dB.
A . 64,2 dB
B . 67,7 dB.
C . 65,8 dB.
D . 65,8 dB.
E 69,7 dB. Vrai.
Question 13
Calculer le niveau global en dB(A) du son de la question précédente.
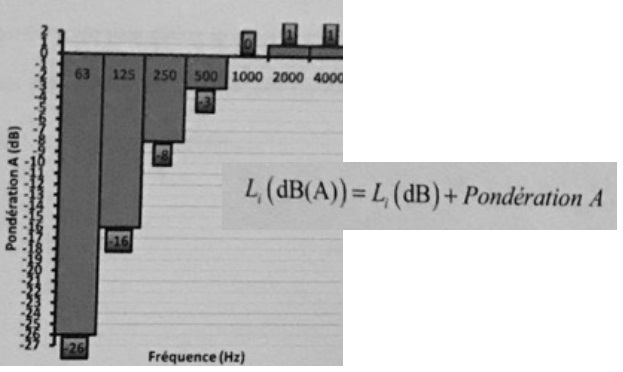
Itotal / I0
= 106,2-2,6 +105,5-1,6+106-0,8+106,2-0,3+106,4+106,1+0,1+106+0,1
=(3,98 10-3 +7,94 10-3+0,158+0,794+2,512+1,58
+1,26) 106=6,31 106.
L = 10 log(6,31 106) =68,0 dB.
A 73,2 dB(A)
B
69,3 dB(A)
C 68,0 dB(A). Vrai.
D 60,8 dB(A).
E 62,1 dB(A).
Question
14
Concernant la campagne de mesure ci-dessous, Léq est égal à :
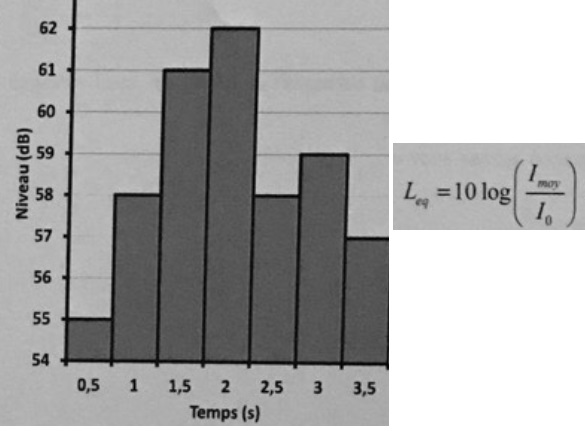
N
= 7 mesures.
Imoy
/ I0 = (105,5 +105,8+106,1+106,2+105,8+105,9+105,7
) / 7=(0,316 +0,63+1,26+1,58+0,63+0,794 +0,50) 106 / 7=0,816
106.
L = 10 log(0,816 106) =59,1 dB.
A
. 67,6 dB.
B.56,5 dB.
C. 54,4 dB
D. 59,1 dB. Vrai.
E.
55,1 dB
Question
15
Si l'on tient compte de la durée d'intégration t utilisée pour effectuer chacune
des N mesures de niveau sonore, le niveau équivalent de la campagne de
mesures de durée Nt
: Léq = 10 log ( Imoy / I0), peut
aussi s'écrire :
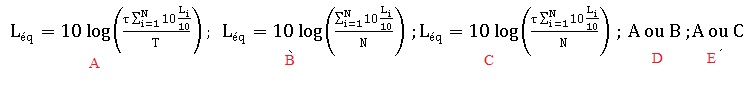
Réponse D.
Question
16. ( suite de la question précédente ).
On peut définir le niveau équivalent sur une période T et le
niveau d'exposition sonore ( SEL) ramené sur 1 s.
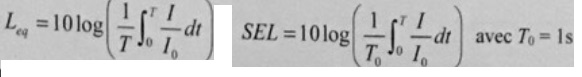
A. Le sel quantifie
la dose d'énergie sonore reçue pendant la période T. Faux..
B.
Le sel quantifie la dose d'énergie sonore reçue pendant 1 s.
C. Le sel quantifie
la moyenne du niveau sonore pendant 1 s.
D. A et C.
E. B et C. Vrai.
|
|
Question 17. Suite de la question précédente.
On
souhaite quantifier la dose de bruit subie par un musicien d'orchestre.
On mesure le niveau équivalent pour chacune des différentes périodes de
la journée.
4 h de répétition tutti ( Léq = 89,3 dB(A) ; 2 h de
répétition par pupitre ( 87,4 dB(A)) ; 1,5 h de concert ( 90,2 dB(A)) ;
1 h de pause ( 63,9 dB(A).
Quelle formule vous semble correcte pour déduire le SEL de la journée ?
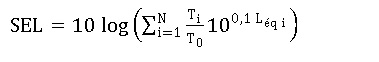 Réponse
B. Réponse
B.
Question 18
Calculer le SEL de l'ensemble de la journée du musicien.
A. 112,4 dB(A)
4 x108,93 +2 x108,74 + 1,5 109,02 +106,39
=(3,40+1,1 +1,57+0,0024) 109=6,07 109.
6,07 109 x3600 = 2,18 1013.
SEL =10 log (2,18 1013 ) =133,4 dB(A).
B.
133,4 dB(A). Vrai.
C.
88,8 dB(A).
D .134,2 dB(A)
E. 89,6 dB(A).
Question 19
Les textes de loi font référence au niveau Lex, 8h qui
ramène la dose de bruit journalière sur une durée de 8 h. Quelle
formule vous semble correcte pour déduire Lex, 8h à partir
du SEL de la journée ?
Léq 8H =SEL-
10 log(8x3600) = SEL-44,6.
A. SEL
/ 8.
B . SEL -9,0.
C . SEL / 28800.
D. SEL-12,3.
E SEL-44,6. Vrai.
Question 20
Calculer Lex, 8h de cette journée.
133,4 -44,6 =88.8 dB(A).
A. 112,4 dB(A)
B . 133,4 dB(A)
C .88,8 dB(A). Vrai.
D . 134,2 dB(A)
E. 89,6 dB(A)
Question 21
Résumé du texte de loi : Léq 8h
<80 dB(A) : aucun danger ; 80 < Léq 8h
<80 dB(A) < 85 dB(A) : mise à disposition de protection.
Léq 8h >87 dB(A) : port de protection obligatoire. Ce
dernier seuil doit tenir compte de l'atténuation apporté par les
protections auditives.
Qu'en déduisez-vous concernant ce professeur ?
A.Le port de protection est
obligatoire. Le seuil de 87 dB(A) ne devrait pas être atteint. Vrai.
B. Le port de
protection est obligatoire. Le seuil de 87 dB(A) pourrait cependant
être atteint.
C.Une
mise à disposition de protections doit être mise en place par l'école
de musique.
D. aucun souci
pareiculier.
E. Léq 8H ne
peut pas être calculé dans ce cas. le texte de loi ne peut pas
s'appliquer.. |
|