Mathématiques, Concours Geipi Polytech 2019

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

Exercice 1.
I-1- QCM
Quel est l’ensemble E des réels x vérifiant 1 − ln 𝑥 ≥ 0 ?
1 > ln x ; e¹ < x. x appartient à ]0 ; e ].
A) E= [1 ;+∞[ ; B) E = [e ;+∞[ ; C) E = ]−∞ ; e] ; D) E = ]0 ; e]. Vrai.
Le plan P est rapporté à un repère orthonormé direct.
On considère les fonctions f et g définies par :
pour tout réel x > 0 , f(x) = exp[(ln(x) / x ] et g(x) = ln(x) / x.
On note C_fla courbe représentative de f dans le plan P.
I-2- Déterminer la limite de f quand x tend vers plus l'infini. Justifier.
Quand x tend vers plus l'infini ln(x) / x tend vers zéro. Par conséquent f(x) tend vers 1 quand x tend vers plus l'infini.
I-3- On en déduit que C_f admet une asymptote Δ. Donner une équation de Δ.
y = 1.
I-4- Déterminer la limite de f(x) quand x tend vers 0⁺. Justifier la réponse.
ln(x) / x tend vers moins l'infini quand x tend vers 0⁺. Par conséquent f(x) tend vers 0 quand x tend vers 0⁺.
I-5- g' désigne la dérivée de g. Calculer, pour tout x > 0, g′(x). Détailler le calcul.
u = ln(x) ; v = x ; u' = 1 / x et v' =1.
g' =(u'v -v'u) / v² = (1 -ln(x) ) / x².
I-6- f ′ désigne la dérivée de f. Pour tout x > 0, on peut écrire f '(x) sous la forme : f '(x) = (1 − ln x) h(x)
Donner l’expression de h(x) en fonction de x. Quel est le signe de h(x) ?
On pose X = ln(x) / x ; u = ln(x) ; v = x ; u' = 1 / x et v' =1.
X' =(u'v -v'u) / v² = (1 -ln(x) ) / x².
f '(x) = X ' e ^X = (1 -ln(x) ) / x² exp(ln(x) / x)). h(x) = exp (ln(x) / x) / x² >0.
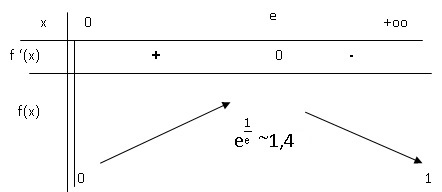
I-7- Dresser le tableau des variations de f sur ]0 ;+∞[ .
I-8 Soit A le point de C_f d’abscisse x_A = e et d’ordonnée y_A .
Donner la valeur exacte de y_𝐴 , puis une valeur approchée de y_𝐴 à 10⁻¹ près.

I-9- QCM
Soit B le point de C_fd’abscisse x_B= 1. T_B désigne la tangente à C_f au point B.
Parmi les affirmations suivantes, lesquelles sont vraies ?
A) T_Ba pour équation y = x-e ; B) T_B a pour équation y = ex
C) T_B a pour équation y = x ; D) T_B passe par le point O.
Coefficient directeur de T_B : f '(1) = 1 ;
T_B passe par le point B( 1 ; 1) ; 1 =1 +b soit b = 0.
I-10- QCM
Soit C le point de C_f d’abscisse x_C= 0,5 et d’ordonnée y_C . Que vaut y_C ?
f(0,5) = exp (2 ln(0,5) =exp(ln(0,5²))= 0,5² = 0,25.
A) y_C = 1/4 ; B) y_C = exp 0,5 ln(0,5)). Faux.
C) y_C = exp (ln(2) / 2). Faux. D) y_C = exp(-2 ln(2)).
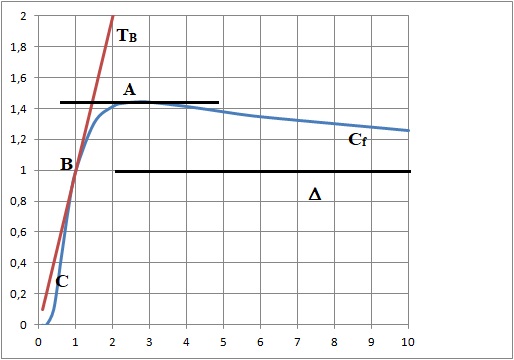
I-11- Placer, sur la figure, les points A, B et C.
Tracer la droite Δ, la tangente T_B , la tangente à C_f au point A. Puis tracer la courbe C_f.

I-12- VRAI-FAUX
Soit m un réel. On s’intéresse au nombre de réels x > 0 vérifiant l’équation :
f(x) = m
Pour chacune des trois assertions suivantes, indiquer si elle est vraie ou fausse.
Aucune justification n’est demandée. Une réponse incorrecte sera pénalisée, une absence de réponse ne sera pas pénalisée.
A) Si m appartient à ]1 ; y_A[ , l’équation a exactement deux solutions. Vrai.
B) Si m < 0 ou m ≥ y_A , l’équation n’admet aucune solution. Faux.
C) Si m = 1, l’équation a exactement deux solutions. Faux.

Exercice 2.
Les deux parties sont indépendantes.
Première partie - QCM
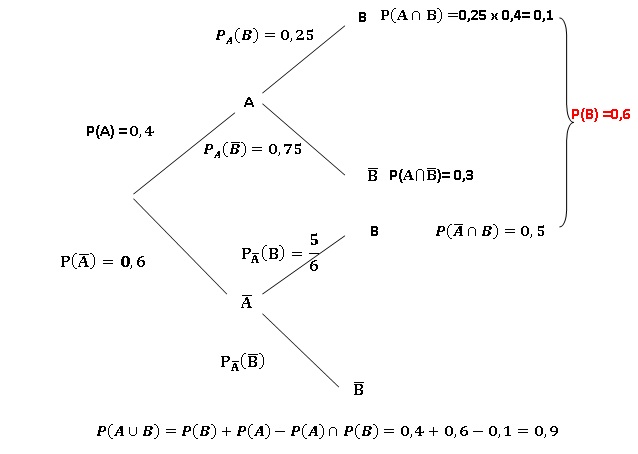
II -1- Lors d’une même expérience aléatoire, deux événements A et B vérifient :
P(A) = 0,4 ; P(B) = 0,6 ; P(A∩ non B)= 0,3.
Parmi les assertions suivantes, lesquelles sont vraies ?
A) P(A ∩ B) = 0,1 ; B) P(A ∩ B) = 0,24
C) P(A∪ B) = 1 ; D) P(A ∪ B) = 0,9.

II -2- X désigne une variable aléatoire suivant la loi uniforme sur l’intervalle [3 ; 18].
Soit P₁ la probabilité que X soit compris entre 5 et 10 sachant que X est strictement supérieur à 4. Que vaut P₁ ?
A) P₁ = 4 / 15 ; B) P₁ = 5 /13 ; C) P₁ = 5 /14; D) P₁ = 1/3.
II -3- Soit l > 0. X désigne une variable aléatoire suivant la loi exponentielle de paramètre l.
Soit P₂ la probabilité que X soit compris entre 2 et 5. Que vaut P₂ ?
P(X < 2)=1-e^-2l ; P(X < 5)=1-e^-5l ; P(2 < X < 5)= e^-2l -e^-5l . Réponse C.
𝐈𝐈𝐈𝐈 -4- Soit l > 0. X désigne une variable aléatoire suivant la loi exponentielle de paramètre l.
Soit P₃ la probabilité que X soit supérieure à son espérance E(X). Que vaut P₃ ?
E = 1 / l ; P₃ = P(X > E) = exp(-l / l) = e^-1. Réponse A.

Deuxième partie.
Soit n un entier naturel non nul. Pour un jeu de dé, qui se joue en n parties, on utilise un seul dé non pipé à six faces. On suppose que les résultats des parties successives sont indépendants. Lors d’une partie, le joueur lance le dé.
• S’il obtient un chiffre pair, alors il reçoit autant d’euros que le nombre apparu sur le dé.
• S’il obtient un chiffre impair, alors il perd m euros, m désignant un réel positif.
On note G_n la variable aléatoire correspondant au gain du joueur lors de la n-ième partie. Ce gain est donc positif ou négatif.
On suppose que le joueur décide de faire une seule partie.
II -5- Compléter le tableau donnant la loi de G₁.

x	2	4	6	-m
P(G₁ = x)	1/6	1 / 6	1 / 6	0,5

II -6- Donner la probabilité P₁ que le joueur ait un gain positif. P₁ = 0,5.
II -7- Donner, en fonction de m, la valeur de l’espérance E(G₁). Détailler le calcul.
E(G₁) = 2 x1 /6 +4 x1 / 6 +6 x 1 /6 -m / 2= 2- 0,5 m.
II -8- Pour quelles valeurs de m a-t-on E(G₁) ≥ 0 ?
2-0,5 m > 0 ; m < 4.
Dans la question suivante, on suppose que le joueur joue successivement deux parties et que m = 4.
II -9- On note G_T = G₁ + G₂ la variable aléatoire correspondant au gain total du joueur à l’issue des deux parties. Calculer la probabilité P₂ que le joueur ait un gain total nul. Détailler le calcul.
P₂ =P(G_T=0) = P(G₁=4) n P(G₂ = -4) + P(G₁= -4) n P(G₂ = 4)=P(G₁=4) x P(G₂ = -4) + P(G₁= -4) x P(G₂ = 4)=0,5 x 1/6 +0,5 x1 /6 = 1 /6.
Dans la suite, n est quelconque.
II-10- Soit X la variable aléatoire égale au nombre de parties où le joueur a un gain positif.
Donner la loi de X. Préciser ses paramètres.
X suit la loi binomiale de paramètre n et 0,5.
II-11- Notons q_n la probabilité que le joueur ait un gain positif à au moins une des n parties.
Donner l’expression de q_n en fonction de n.
q_n = 1-0,5ⁿ.
II-12- Déterminer le nombre minimal n₀ de parties que le joueur doit faire pour que la probabilité précédente soit strictement supérieure à 0,99. Détailler les calculs.
q_n > 0,99 ; 1-0,5ⁿ > 0,99 ; 0,5 ⁿ < 0,01 ; n log (0,5) < log (0,01) ; -0,301 n < 2 ; n > 2 / 0,301 ; n₀ = 7.

Exercice 3.
La première question est indépendante.
III-1- VRAI-FAUX
On considère, dans l’espace, deux droites D et D' et deux plans P et P′.
Pour chacune des assertions suivantes, indiquer si elle est vraie ou fausse. Aucune justification n’est demandée. Une réponse incorrecte sera pénalisée, une absence de réponse ne sera pas pénalisée.
A) Si D et D′ ne sont pas parallèles, alors elles sont sécantes. Faux.
B) Si D et D′ sont sécantes, alors elles sont coplanaires. Vrai.
C) Si D est orthogonale à P, alors elle est orthogonale à toute droite contenue dans P. Vrai.
D) Si P et P′ sont parallèles, alors toute droite de P est parallèle à toute droite de P′. Faux.
Dans l’espace rapporté à un repère orthonormé, on considère :
• les points A, B et C de coordonnées respectives :
A (1 ; 1 ; 1) ; B( 1 ; 1 ; 1,5) ; C(2 ; 1 ; 1)
• le plan P d’équation cartésienne : x − y + 2 z − 3 = 0.
III-2- Parmi les points A, B et C, lesquels appartiennent au plan P ?
x_A -y_A +2 z_A -3 =1-1+2-3 = -1, différent de zéro, A n'appartient pas au plan P.
x_B -y_B +2 z_B -3 =1-1+2x1,5-3 =0, B appartient au plan P.
x_C -y_C +2 z_C -3 =2-1+2-3 = 0, C appartient au plan P.
III-3- QCM
Parmi les vecteurs suivants, lesquels sont normaux au plan P ?
Coordonnées d'un vecteur normal au plan P : (1 ; -1 ; 2).

III-4- Soit D la droite passant par le point A et orthogonale au plan P.
Donner un système d’équations paramétriques de la droite D.
Coordonnées d'un vecteur directeur de la droite D : (1 ; -1 ; 2).
La droite passe par le point A (1 ; 1 ; 1).
Par suite x = t+1 ; y = -t+1 ; z = 2t +1 avec t réel.
III-5- Soit K le projeté orthogonal du point A sur le plan P.
Déterminer les coordonnées (x_K ; y_K ; z_K) du point K. Justifier la réponse.
Le vecteur AK et le vecteur de coordonnées (1 , -1 ; 2) sont colinéaires.
Par suite x_K-1 = k' ; y_K-1 = -k' ; z_K -1 = 2k'.
x_K = k' +1; y_K = -k' +1 ; z_K = 2k'+1.
K appartient au plan P : k' +1+k'-1+2(2k'+1)-3=0 ; k' = 1 / 6.
K( 7 /6 ; 5 / 6 ; 4 /3).
III-6- Donner les coordonnées du vecteur BC.
(x_C-x_B ; y_C-y_B ; z_C-_zB) soit (1 ; 0 ; -0,5).
III-7- Soit P₁ le plan passant par le point A et orthogonal à la droite (BC).
Donner une équation cartésienne du plan P₁.
Coordonnées d'un vecteur orthogonal à P₁ ( 1 ; 0 ; -0,5) : x +0 y -0,5 z +d = 0 ; x -0,5z +d = 0.
A appartient à ce plan : x_A -0,5Z_A +d = 0 ; 1-0,5 +d = 0 ; d = -0,5.
x -0,5z -0,5 = 0.
III-8- QCM
Parmi les systèmes paramétriques suivants, lesquels représentent la droite (BC) ?
Coordonnées d'un vecteur directeur de la droite (BC) : (1 ; 0 ; -0,5) ou encore (2 ; 0 ; -1).
La droite passe par B(1 ; 1 ; 1,5) : x=2t +1 ; y =1 ; z = -t +1,5 avec t réel.
La droite passe par C(2 ; 1 ; 1) : x =2 t'+2 ; y = 1 ; z = - t' +1 avec t' réel.

III-9- Soit H le projeté orthogonal du point A sur la droite (BC).
Donner les coordonnées (x_H, y_H, z_H) du point H.
Le vecteur AH ( x_H-1 ; y_H-1 ; z_H-1) et le vecteur BC (1 ; 0 ; -0,5) sont orthogonaux.
x_H-1 -0,5(z_H-1) = 0 soit x_H-0,5 z_H-0,5 = 0.
H appartient à la droite (BC) : x_H=2t +1 ; y_H =1 ; z_H= -t +1,5.
2t +1 -0,5(-t+1,5) -0,5 =0 ; 2,5 t =0,25 ; t = 0,1.
x_H=0,2 +1=6 /5 ; y_H =1 ; z_H= -0,1 +1,5 = 7 / 5.

III-10- Déterminer une équation du plan P₂ passant par le point A et parallèle à P. Justifier la réponse.
Plans parallèles : équation de P : x − y + 2 z − 3 = 0
équation de P₂ : x − y + 2 z +d = 0
A appartient à P₂ : x_A -y_A +2z_A +d = 0 ; 1-1+2+d=0 ; d=-2.
x − y + 2 z -2 = 0
III-11- Calculer la distance d entre les plans P et P₂. Détailler le calcul.
A(1 ; 1 ; 1) ; K( 7 /6 ; 5 / 6 ; 4 /3).
AK² =(7 / 6 -1)² +(5 / 6 -1)² +(4 / 3-1)² = 1 /6 ; AK = 1 / 6^½.
III-12- VRAI-FAUX
Pour chacune des assertions suivantes concernant les positions relatives des droites (BC) et (HK), indiquer si elle est vraie ou fausse. Aucune justification n’est demandée. Une réponse incorrecte sera pénalisée, une absence de réponse ne sera pas pénalisée.
A) Elles sont sécantes Vrai ; B) Elles sont parallèles
C) Elles sont orthogonales vrai ; D) Elles sont coplanaires Vrai.
K( 7 /6 ; 5 / 6 ; 4 /3).

Exercice 4.
Les trois parties sont indépendantes.
Dans tout l’exercice, a désigne un nombre réel strictement supérieur à 1.
Le plan complexe est rapporté à un repère orthonormé direct.
Soient A et B les points d’affixes respectives :
z_𝐴 = 2 + 2 i (a² − 1)^½ et z_𝐵= 4
On définit les points C, D, H par :
• C est le symétrique de A par rapport à l’axe des abscisses.
• D est le symétrique de A par rapport au point O ;
• H est le projeté orthogonal de B sur la droite (AD).
On note z_𝐶, z_𝐷 et z_𝐻 les affixes respectives des points C, D et H.
Première partie.
Dans cette partie, on suppose que a = 2.
IV-1- Écrire la forme algébrique de z_𝐴 . Donner son module |z_𝐴|.
Puis écrire la forme exponentielle de z_𝐴 .
z_𝐴 = 2 + 2 i 3^½ ; |z_𝐴| = (2² +(2 *3^½)²)^½=(4 +12)½ ; |z_𝐴| = 4.
z_A / |z_A| = 0,5 + i 3^½/ 2 = cos (p/3 + i sin (p /3). z_A = 4 exp (ip/3).
IV-2- Donner la valeur de z_𝐶 sous forme algébrique et exponentielle.
z_C = 2 - 2 i 3^½ ; z_C = 4 exp(-ip/3).
IV-3- QCM
Parmi les expressions suivantes, laquelle correspond à la forme exponentielle de z_D ?
z_C = 4 exp (i 4p/3) = 4 exp (- i 2p/3) Réponse C.
IV-4- Sur la figure, placer les points A, B, C et D..
Faire apparaître la construction qui vous permet de placer les points correctement.

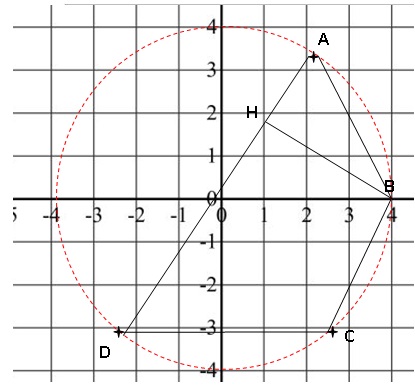
IV-5- Donner la nature précise du triangle OAB et du quadrilatère ABCD.
Le triangle OAB est équilatéral.
ABCD est un trapèze.
IV-6- Justifier géométriquement que z_H = 0,5 z_A. En déduire la forme algébrique de z_H. Placer le point H sur la figure
HB est la hauteur d'un triangle équilatéral, c'est donc la médiatrice du segment [OA].
OH = HB =0,5 OA. z_H = 1 + i 3^½ ;
IV-7- QCM
Soit A l’aire, en unités d’aire, du quadrilatère ABCD. Quelle est la valeur exacte de A ?
(BC + AD x HB / 2 avec BC = AB = AO = 4 ; AD = 8 et BH = 2 x 3^½.
A = 12 x3^½. Réponse C.

Dans la suite, a est quelconque
Deuxième partie.
IV-8- Notons ℓ₁ et ℓ₂ les longueurs respectives des diagonales [OB] et [AC] du losange OABC .
Donner la valeur exacte de ℓ₁. Donner une expression de ℓ₂ en fonction de a.
OB =4 ;
OA = [( 2² + 4 (a² − 1)]^½ =2a.
AC = 2 (OA² - (0,5 OB²)^½ =2(4a²-4)^½ = 4(a²-1)^½.
IV-9- Pour quelle(s) valeur(s) de a le quadrilatère OABC est-il un carré ? Justifier la réponse.
Les diagonales d'un carré sont égales : 4 = 4(a²-1)^½.
16 = 16(a²-1) ; 16a² =32 ; a = ±2^½ ; or a >0 ; a = 2^½.
Troisième partie.
Soient (E) et (E′) les équations d’inconnue complexe z :
(E) ∶ z²– 4 z + 4 a² = 0 (E′) ∶ z³ – 4 𝑧² + 4 a² z = 0
IV-10- Justifier que l’équation (E) admet deux racines complexes non réelles.
Discriminant D = 16-16a² = 16 (1-a²) avec a > 1.
Le discriminant étant négatif, l'équation (E) admet deux racines complexes.
IV-11- On note z₁ et z₂ les deux solutions de l’équation (E).
Donner les expressions de z₁ et z₂ en fonction de a.
z₁ =( 4+4i(1-a²)^½ ) / 2 = 2+2i(1-a²)^½ et z₂ = 2-2i(1-a²)^½.
IV-12- En déduire l’ensemble ℰ′ des solutions de l’équation (E'′).
z³ – 4 𝑧² + 4 a² z =z( z²– 4 z + 4 a² )=0.
Solutions : 0 ; 2+2i(1-a²)^½ et z₂ = 2-2i(1-a²)^½.