Fibre
optique, chute, manège, acide oxalique, Concours Geipi Polytech 2019
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
|
Fibre
optique.
Les fibres optiques constituent un élément
essentiel de la révolution des télécommunications. Cette technologie
augmente considérablement le débit des connexions Internet
de 20 mégabits par seconde, à 100 mégabits par seconde. C’est par ce
moyen que circulent plus de 80%
des informations du trafic mondial longue distance. Les parties 1, 2 et
3 sont indépendantes.
Données :
Vitesse de la lumière dans le vide c = 3,00×108 m.s-1.
Vitesse de la lumière dans un milieu d’indice v = c / n.
Indice de l’air n0 = 1,000
Constante de Planck h = 6,63×10-34 m2.kg.s-1.
1 eV = 1,6×10-19 J
1re
partie : Parcours du rayon dans une fibre optique cylindrique
La fibre utilisée est constituée :
• d’un coeur d’indice n2 = 1,510,
• d’une gaine d’indice n1 = 1,495.

Un rayon incident se propage dans l’air dans un plan axial à la fibre
et arrive en A sous un angle d’incidence i0. La réfraction
est définie par la relation de Descartes : n0 sin(i0)
= n2 sin (r0).
On note i1 l’angle que fait le rayon avec la normale
séparant la gaine
du coeur en B.
Afin que la totalité du rayon lumineux soit réfléchit, l’angle i1
doit
être supérieur à 81.92 °.
I-1- Dans ce cas
limite, calculer l’angle réfracté r0(limite) en A et
l’angle incident i0(limite) en A.
Dans le triangle rectangle AOB : r0 + i1 = 90° ; r0
limite =90-81,92 = 8,08°.
sin i0 limite = n2 sin r0 limite =
1,510 sin 8,08 =0,2122 ; i0 limite = 12,25°.
I-2- Comment régler
i0 pour que la totalité du rayon lumineux soit
réfléchie en B ?
i0 doit etre compris entre 0° et 12,25°.
I-3- Calculer le
temps de parcours de la lumière pour parcourir une
fibre de Lf =100 km lorsque i0=0°.
t = Lf n2 / c = 1,00 105
x1,510 / (3,00 108) =5,03 10-4 s.
I-4- Exprimer puis
calculer le rapport tABC / tAOC en fonction de r0(limite)
entre le temps tABC de parcours de
lalumière lors du chemin ABC et le temps tAOC du parcours du
chemin AOC.
tAOC = AC / v = 2AO / v ; tABC = 2AB / v ; tABC / tAOC =
AB / AO = 1 / cos r0 limite = 1 / cos 8,08 =1,010.
I-5-
En déduire le temps de parcours lorsque i0 = i0(limite).
tABC = 1,01 x 5,03 10-4 = 5,080 10-4 s.
I-6- Une variation
de i0 engendre donc une incertitude sur le temps de
parcours de la forme t0 ± Δt0.
Calculer t0 et Δt0.
t0 = (503 +508) / 2 = 505,5 µs.
Δt0 = (5,08 -5,03) 10-4
= 2,5 10-6 s = 2,5 µs.
2e partie : Etude de l’atténuation de transmission
L'atténuation de puissance subie par le signal lors du parcours d’une
distance L suit la relation :
aL =
-10 log ( Puissance sortante / Puissance entrante).
Le tableau ci-dessous donne les extrémums de la courbe a = f(l) pour notre fibre.
Longueur
d'onde (nm)
|
Atténuation
a
( dB / km)
|
850
|
3,0
|
1310
|
0,4
|
1400
|
2,0
|
1550
|
0,2
|
I-7- Quelle est la
longueur d’onde la mieux adaptée à la transmission
de l’information dans cette fibre optique ?
La longueur d'onde la plus adaptée correspond à la plus faible
atténuation ( 1500 nm).
I-8- Donner le
domaine de l’onde électromagnétique correspondant à
cette longueur d’onde.
1550 nm appartient au proche infrarouge.
I-9- On doit
amplifier à nouveau le signal dès que la puissance devient
inférieure à 1% de sa puissance incidente. Quel est le nombre minimal
d'amplificateurs
nécessaires pour une liaison Brest- Strasbourg d’environ 1000 km ?
log ( puissance sortante / puissance incidente) = log( 0,01) = -2.
L = 10 x 2 / 0,2 =100 km.
Le nombre minimal d'amplificateurs estégal à 10.
3e
partie : Etude de la source Laser
I-10- Donner 2
caractéristiques principales du laser qui explique son
utilisation pour générer le faisceau lumineux se propageant dans la
fibre.
Monochromatique et très directif.
I-11- Quelle est la
relation liant l’énergie Ephoton du photon à sa
longueur d’onde. Calculer cette énergie en eV pour une onde
électromagnétique de longueur d’onde 1550 nm.
E = hc / l
=6,63 10-34 x3,00 108 / (1550 10-9)
=1,283 10-19 J soit 1,283 10-19 / (1,6 10-19)
=0,80 eV.
|
|
Exercice
4.
Deux
étudiants, Sarah et Gaspard, cherchent à déterminer la profondeur du
puits d’accès d’une mine. Celui-ci est vertical et suffisamment profond
pour que le fond à la profondeur H soit invisible. Gaspard propose de
lâcher une pierre dans le puits et de déduire du temps de chute la
profondeur du puits.
Il analyse l’expérience en ne tenant compte de la seule pesanteur. Soit
t le temps écoulé à partir du moment où la pierre est lâchée à vitesse
nulle au-dessus du puits, z(t) la position de la pierre à l’instant t
et v(t) sa vitesse.
Données :
Accélération de pesanteur g = 9,81 m.s-2. Vitesse du son c =
343 m.s-1.
Masse de la pierre m = 100 grammes. z=H fond du puits ; z=0 surface.
IV-1- En faisant
l’hypothèse que seule la force de pesanteur agit sur la pierre et en
appliquant la 2ème loi de Newton, exprimer l’accélération
verticale a.
On choisit un axe vertical orienté vers le bas, origine : partie haute
du puits. a = g = 9,81 m s-2.
IV-2- En déduire
les expressions de la vitesse v(t) et la position z(t) au cours de la
chute.
La vitesse est une primitive de l'accélération et la vitesse initiale
est nulle : v(t) = 9,81 t.
La position est une primitive de la vitesse et position initiale est
nulle : z(t) = 4,905 t2.
Soit t1 le temps de chute mis par la pierre pour atteindre
la profondeur H. On peut exprimer t1 de la sorte
t1 = a H½ avec a=0.452 SI.
IV-3- Donner
l’expression littérale de a.
H = ½gt12 ; t1 = (2 H / g)½
; a =(2 / g)½.
On mesure la durée tmes= 19,17 s entre le moment du lâché et
le moment où le son de choc est perçue à la surface.
IV-4- Exprimer ce
temps en fonction de t1 et du temps t2 mis pour
que le choc soit perçu, puis exprimer ce temps en fonction de H.
tmes = t1 +t2 = a H½ + H/ c.
IV-5-
On peut reformuler l’équation précédente sous la forme H + ß H½
+g = 0 = 0 avec ß
= 155 SI et g =
−6575 SI. Donner les expressions littérales de β et g ainsi que leurs unités.
a H½ + H/ c +tmin
= 0 ; H +a c H½ + c tmin
= 0.
ß = a c ( m½); g
= c tmes (mètre).
IV-6-
Calculer la profondeur H du puits en résolvant numériquement l’équation
en H.
H +155 H½ -6575 =0.
On pose X2 = H ; X2 +155 X -6575 = 0 ; D =1552 + 4 x6575
=50325 ; D½
=224,33.
On retient la valeur positive X = (-155 +224,33) / 2 = 34,67 ; H = 34,672
~1200 m.
Sarah
estime qu’il faudrait prendre en compte, en plus de la pesanteur, une
force de frottement f. En appliquant ses cours de mécaniques des
fluides, elle modélise cette force de la manière suivante :
- sa direction est celle du mouvement, - son sens est opposé au
mouvement, - sa norme a pour expression f = kv2 avec k =
1,190 10−3 SI.
IV-7- En appliquant
la 2e loi de Newton, exprimer l’accélération verticale a′ .
mg -kv2 = m dv/dt = m a' ; a' = g-k / m v2..
La vitesse limite vlim est atteinte par la pierre lorsque
l’accélération devient nulle.
IV-8- Exprimer puis
calculer vlim .
mg -kvlim2 =0 ; vlim
= (m g / k)½ =(0,100 x9,81 / (1,190 10-3)½=28,7
m / s.
Sarah considère que le mouvement est en
fait constitué de deux phases :
- une première de l’instant t= 0 à l’instant T = vlim / g où
la force f ne s’exerce pas,
- une seconde phase pour t supérieur à T où la vitesse est constante et
égale à vlim.
IV-9- Définir le
mouvement de la pierre lors la première phase puis lors la seconde
phase.
Première phase : mouvement rectiligne uniformément accéléré.
Seconde phase : mouvement rectiligne uniforme.
IV-10- La
profondeur atteinte z(t) après une durée de chute t > T est telle
que :
z(t) = A T2 +B (t-T) avec A = 4.90 SI et B = 28.72 SI.
Donner les expressions des coefficients A et B ainsi que leurs unités.
z(t) = ½g T2 + vlim(t-T).
A = 0,5 g ( m s-2) ; B = vlim ( m / s).
IV-11- Exprimer
l’estimation H'de la profondeur du puits en fonction de la durée
mesurée tmes entre le lâché de la pierre et le bruit de son
arrivée. Calculer H'.
t = tmes-H'/c.
H' = AT2 + B(tmes-H'
/ c-T) ; H' ( 1+B / c)= AT2+B(tmes-T) / (1
+B/ c).
H' = [4,90 x(28,7 /9,81)2+ 28,72 (19,17 -28,7 / 9,81)] / (1
+28,72 / 343) =(41,94+466,54) / 1,084 =469
m.
|
|
Exercice 2.
L’acide oxalique est un
diacide carboxylique de formule semi développée HOOC-COOH.
Présent à l’état naturel
dans de nombreux végétaux, il est très bien toléré par l’organisme dans
les aliments courants. Toutefois,
consommé en trop grande quantité ou par des sujets sensibles, il peut
conduire à certaines pathologies,
voire être mortel à forte dose.
Données :
M(H) = 1 g.mol-1 ; M(C) =
12 g.mol-1 ; M(O) = 16 g.mol-1 ; M(K) = 39 g.mol-1 ; M(Mn) = 55 g.mol-1
;
pKA1 (acide oxalique) =
1,25 ; pKA2 (acide oxalique) = 4,25
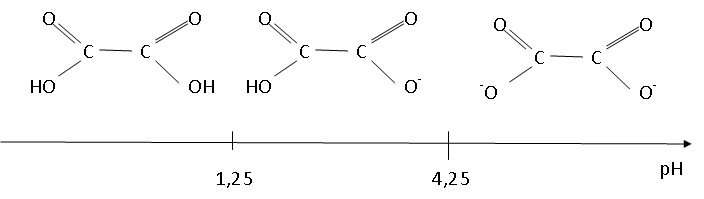
II-1- Donner la formule
développée de la molécule d’acide oxalique.
II-2- Préciser sur le
diagramme de prédominance la nature des espèces prépondérantes.
On se propose de doser
une solution aqueuse d’acide oxalique par une solution titrée de
permanganate de potassium (KMnO4) à 1,00
×10-3 mol.L-1.
II-3- Calculer la masse
de permanganate de potassium à dissoudre dans 100,0 mL d’eau pure pour
obtenir une concentration de 1,00
×10-3 mol.L-1 = 1000 μmol.L-1.
M(KMnO4) =39 +55 +4 x16 = 158 g / mol ; 158 x1,00 10-4 = 0,0158 g.
Cette solution est
colorée par l’ion permanganate, ce qui permet d’en suivre la
concentration par spectrophotométrie à
l’aide de la courbe d’étalonnage A = f(C) ci-dessous.
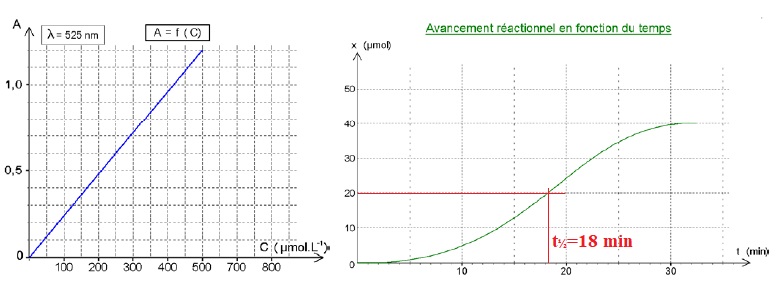
Dans un réacteur thermostaté, on introduit 100,0 mL de la solution de permanganate de potassium de concentration 1,00 ×10-3 mol.L-1,
à 100,0 mL d’une solution d’acide oxalique de concentration inconnue.
La réaction commence alors entre l’acide oxalique et l’ion permanganate
; cette réaction est totale :
5 H2C2O4 + 2 MnO4- + 6 H+ = 10 CO2 + 2 Mn2+ + 8 H2O
II-4- Préciser les deux couples oxydoréducteurs intervenant dans cette réaction.
MnO4- / Mn2+ et CO2 / H2C2O4.
On déclenche un
chronomètre et on suit l’absorbance de la solution à λ = 525 nm en
fonction du temps. On en déduit l’évolution de l’avancement en fonction
du temps de réaction (courbe ci-dessus).
II-5- Donner la valeur du temps de demi-réaction :18 min.
II-6- Déterminer la vitesse de réaction à t = 20 minutes.
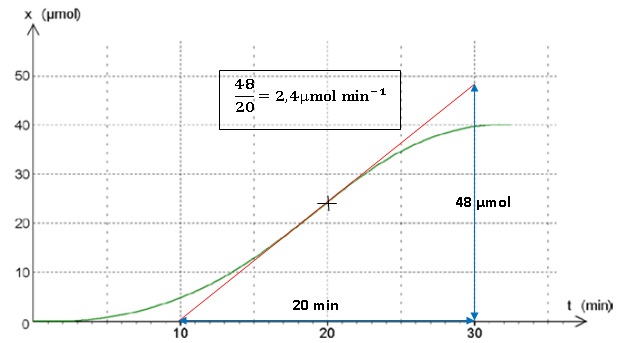
II-7- Compléter le tableau d’avancement.
t
|
x
|
H2C2O4 |
MnO4- |
H+ |
CO2 |
Mn2+ |
H2O
|
0.
|
0
|
200
|
100
|
excès
|
0
|
0
|
escès
|
t ---> oo
|
40
|
200 -5 x40 = 0
|
100-2x40 = 20
|
excès
|
10x40 =400
|
2 x40 = 80
|
excès
|
II-8- Donner la valeur de l’absorbance mesurée à t = 0 puis pour t → ∞ .
Concentration initiale de l'ion permanganate : 1,00 10-3 x 100 / 200 = 5 10-4 mol/L = 500 µmol / L.
Concentration finale de l'ion permanganate : 100 µmol / L
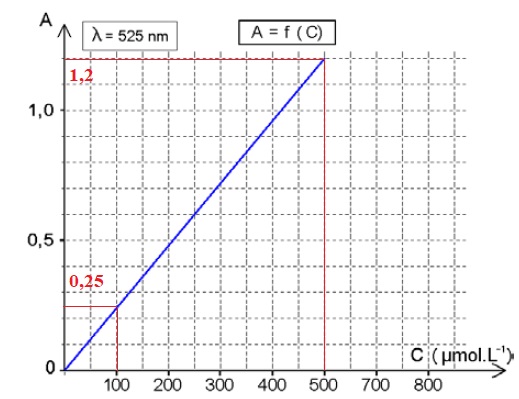
A (t=0) = 1,2 ; A ( t --> oo) =0,25.
II-9- Désigner l’allure de la courbe expérimentale A = f(t).

La solution finale contient encore des ions permanganate ( en excès).
L'absorbance n'est pas nulle. Les courbes 1, 2 et 5 ne sont pas
retenues.
L'absorbance décroît comme la concentration en ion permanagante. La courbe 3 ne convient pas.
L'avancement n'est pas une fonction linéaire du temps : la courbe 6 ne convient pas.
Donc courbe 4.
II-10- Déterminer la concentration de la solution d’acide oxalique de départ.
Quantité d'ion parmanganate ayant réagit : 80 µmol.
Quantité de matière d'acide oxalique : 80 x2,5 = 200 µmol contenue dans 100 mL
Concentration initiale de l'acide oxalique ; 2,00 10-4 / 0,100 =2,00 10-3 mol / L.
|
|
Exercice 3.
Le petit
Auguste est emmené par ses parents faire un tour de manège. Il veut
monter sur un cheval de bois.
Le manège est représenté par un disque de centre O tournant dans le
plan horizontal 0xy autour de l’axe Oz à la vitesse angulaire constante
ω.
Le repère Oxyz est donc le repère de référence fixe. Le sens de
rotation du manège est la senestre, soit le sens trigonométrique. Le
référentiel est supposé galiléen. On note T la période du mouvement : T
= 2π /ω.
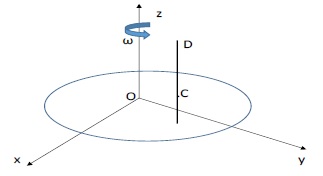
Le cheval de bois, noté C, est situé à la distance R de l’axe de
rotation. On assimilera C à un point matériel. Les équations horaires
de ses coordonnées x et y en fonction du temps t sont : x = R cos(ωt) ;
y = R sin(ωt)
C est de plus animé d’un mouvement vertical oscillant le long d’un axe
D d’amplitude A.
L’équation horaire de sa coordonnée z en fonction du temps t est : z =
A sin(ωt) + A
Ainsi, à t = 0, on a z = A, etc…
On suppose, de plus, qu’à t = 0, le manège a été démarré et tourne en
régime établi.
III-1- Exprimer, en
fonction de la période T, le temps t1 où le maximum de
hauteur zmax est atteint.
sin ( wt1)
= 1 soit wt1= ½p ; t1 = p / (2w) = T / 4.
III-2-
Exprimer, en fonction de la période T, le temps t2 où le
minimum de hauteur zmin est atteint.
sin ( wt2) = -1 soit wt2=
1,5p ; t2
= 3p / (2w) = 3T / 4.
III-3-
Calculer T, t1 et t2 lorsque ω = π/10 rad.s-1.
T = 20 s ; t1 = 5 s ; t2 = 15 s.
III-4- Sur quelle
forme peut-on dessiner la trajectoire de C ?
cercle ;
cône, cylindre ; disque ; sphère.
Auguste veut attraper le pompon, une petite poupée accrochée au plafond
du manège. Le pompon est repéré par sa position (xp , yp
,3A). Il ne peut le faire que si le cheval se situe à sa hauteur
maximale.
III-5- A quel
endroit, le propriétaire du manège doit-il accrocher le pompon ? Donner
pour cela les coordonnées xp et yp du pompon.
xp = R cos ( p
/ 2) = 0 ; yp = R sin ( p
/ 2) = R.
III-6-
Exprimer les coordonnées Vx, Vy et Vz
du vecteur vitesse V du cheval de bois C.
Vx = dx /dt = -Rw sin(ωt)
; Vy
= dy /dt = Rw cos(ωt)
; Vz
= dz /dt = Aw cos(ωt).
On décompose V en une somme de deux vecteurs, sa
composante dans le plan Oxy et sa composante suivant Oz.
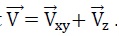
III-7- Donner
l’expression de la norme Vxy. Montrer qu’elle est
indépendante du temps.
Vxy = ( R2 w2 sin2(wt )+R2 w2 cos2(wt )) = Rw.
III-8-
Exprimer les coordonnées ax, ay et az
du vecteur accélération a du cheval C.
ax
= dVx /dt = -Rw2 cos(ωt)
; ay
= dVy /dt = -Rw2 sin(ωt)
; az
= dVz /dt = -Aw2 sin(ωt).
On pose de même 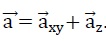
III-9- Dessiner les
vecteurs 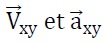 au point Q(-R, 0, A). (choix des
échelles libre). au point Q(-R, 0, A). (choix des
échelles libre).
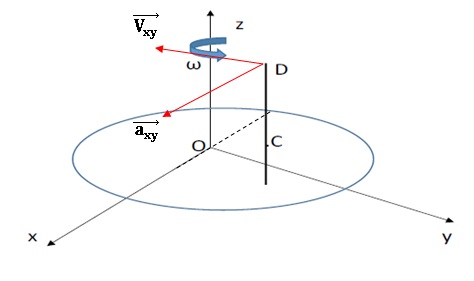
III-10- Comment
qualifie-t-on la composante axy de l’accélération pour un
tel mouvement ?
Radiale, centripète ; radiale centrifuge
; tangentielle ; de direction constante ;
de norme constante.
|
|