Mathématiques,
suites, nombres complexes, fonctions, Concours Avenir 2019
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
|
Réponse exacte : 3 points ; réponse fausse
: -1.
Répondre à 45 questions sur les 60 proposées.
Durée 1 H 30 min.
Suites numériques.
1. Soit (un)
une suite arithmétique telle que u10 = 12 et u15
= 8.
Que vaut la raison r de (un) ?
a. r = 0,6 ; b. r = −0,6 ; c. r = −0,8 vrai ; d. r = −1,2.
u10 = u0 +10r ; u15 = u0 +15r ; u15 - u10 =5r ; r
=(8-12) / 5 = -0,8.
2. Soit (un) une suite
arithmétique telle que :
u2018 = 12 et (u2018 +u2020 ) /2 =12,5.
Que vaut la raison r de (un) ?
a. r = 0,5 vrai ; b. r = 1; c. r = −1; d. r = −0,5.
u2018 =
u0 +2018 r =12; u2020
= u2018 +2 r ; u2018
+ u2020 =24 +2r = 25 ; r =0,5.
3. Soit (un) la suite
arithmétique de premier terme u0 = −10 et de raison 2 ; soit
(vn) la suite géométrique de premier terme v0 = 1
et de raison 2 ; soit enfin (wn) la suite définie sur N par
: wn =(un +vn) / 2..
La somme u9 +v9 +w9 est égale à :
a. 260 ; b. 520 ; c. 780 vrai ; d. 1 560.
u9 = -10 +2 x9 = 8 ; v9 = 1 x29 =512 ;
w9 =(8+512) / 2 = 260 ; u9 + v9 + w9 =8+512+260=780.
4. Soit (un)
une suite géométrique de raison 2 et (vn) la suite définie
par vn = 2un .
On peut alors affirmer que :
a. (vn)
est une suite géométrique de raison 2. Vrai.
b. (vn)
est une suite géométrique de raison 4.
c. (vn)
est une suite arithmétique de raison 2.
d. (vn)
est une suite arithmétique de raison 4.
un = u0 x 2n ; vn = 2u0 x 2n
= v0 x2n.
5. Soit (un) une suite
géométrique de raison q non nulle et (vn) la suite définie
par vn = un+1 −un.
On peut alors affirmer que :
a. (vn)
est une suite géométrique de raison q. Vrai.
b. (vn)
est une suite géométrique de raison q −1.
c. (vn)
est une suite géométrique de raison q(q −1).
d. (vn)
est une suite arithmétique de raison q.
un = u0 x qn. un+1 = u0 x qn+1.
vn = u0
( qn+1-qn)
= u0 ( q-1) qn=
v0 qn.
6. Soit (un) la suite à
valeurs strictement positives définies sur N par u0 = 2 et
pour tout n ∈N : ...............
Il doit manquer une
information.
On définit également la suite (vn) par pour tout n ∈ N :
vn =un −1/ un.
La suite (vn) est :
a. géométrique de
raison 2 ;
vn = v0 2n =un −1/ un ; un =un
−1 / (v0 2n
)=[un −1 / (2v0 )] 1/2 n-1.
u1 =[u0
/ (2v0
)] =1/v0 .................
b. géométrique de raison ½ ;
vn = v0
(1 / 2)n =un −1/ un ; un =un
−1 / v0 2n
.
u1 =u0 / v0 2 = 1 / v0 ;
c. arithmétique de raison −1;
vn = v0
+(-1)n =un −1/ un ; un =un
−1 / ( v0 +(-1)n)
u1 =u0 /
( v0 -1) = 2 /(v0-1) ;
.....................
d.
arithmétique de raison 2.
vn = v0
+2n =un −1/ un ; un =un
−1 / ( v0 +2n).
u1
=u0 / ( v0 +2) = 2 /(v0+2) ;
.................
7. Soit (vn)n>0 la suite
définie par u0 = −1 et pour tout n ∈N :
un+1 = 2un +n +4.
On définit également sur N la suite (vn) par vn =
un +n+a. Pour quelle valeur de a la suite (vn)
est-elle géométrique?
a. 2 ; b. -2 ; c. 2,5 ; d. 5
; vrai.
vn+1 = 2un
+n +4 +n+1+a =2un
+2n +5 +a = 2(un+n+(a+5)2)).
(a+5) / 2 = a ; a+5 = 2a ; a = 5.
vn+1 = 2(un+n+a) = 2 vn.
8. Soit (un)
définie sur N telle que, pour tout n entier naturel non nul : un+1
= un / (2n) +2n +2. On a alors :
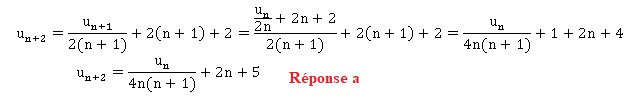
|
|
.
.
|
|
Géométrie
plane et nombre complexes.
Pour les questions 9, 10 et 11, on considère l’algorithme suivant :
Variables
x, y, z : nombres réels
Début algorithme
Saisir x, y, z
Si (x −2)2 +(y +5)2 = z2 alors :
Afficher « Vrai »
Sinon :
Afficher « Faux »
Fin algorithme
9. Que permet de
faire cet algorithme?
a. Tester si un
point appartient à une droite.
b. Tester si un
point est sur un côté d’un triangle.
c. Tester si un
triangle est rectangle.
Il faudrait pour cela que x >2 ; y > -5 et z >x-2 ; z >y+5.
d. Tester si un
point appartient à un cercle. Vrai.
Cercle de centre (2 ; -5) et de rayon |z|.
10. Si
l’utilisateur de cet algorithme entre une valeur négative pour z, alors
:
a. On obtient
toujours « Vrai », quelles que soient les valeurs de x et de y.
b. On obtient un
message d’erreur car l’algorithme ne fonctionne pas.
c. On obtient
toujours « Faux », quelles que soient les valeurs de x et de y.
d. L’affichage
dépend des valeurs de x et de y. Vrai.
11. Dans quel cas
obtient-on « Vrai » ?
a. x = 3, y = 4, z
= 5 ;
(3-2)2 +(4+5)2 =82 diffère de 52 = 25.
b. x = 1, y = 1, z = 2 ;
(1-2)2 +(1+5)2 =37
diffère de 22 = 4.
c.
x = 2, y = −5, z = −3 ;
(2-2)2 +(-5+5)2 =0
diffère de (-3)2 = 9.
d.
x = 5, y = −1, z = 5. Vrai.
(5-2)2 +(-1+5)2 =25
égal à 52 =25.
12.
Un carré a une aire égale à 48 cm2. La longueur de l’une de
ses diagonales est égale à :
a. 4x6½
cm ; Vrai.
côté du carré : 48½ = 4 x3½
; diagonale : 4 x3½ x2½ = 4 x6½.
b. 8x3½ cm ;
c. 8x6½ cm ; d. 4x3½ cm.
13. On note j un
nombre complexe, solution de l’équation 1+z +z2 = 0.
On peut affirmer que (j+j2 +j3)3 est
égal à :
a. 0 vrai ; b. 1; c. j ; d. j2.
j3(1+j +j2)3
avec 1+j +j2 = 0.
14.
La partie réelle du nombre complexe 2i(1+icos p/3 +i sinp/3) est égale à :
a. 3 ; b. −2−3½ ; c. 1,5 ; d. 1+3½/2.
2i +2i2cos p/3 +2i2 sinp/3= 2i- 2cos p/3 - 2sinp/3 ;
partie réelle : -2 cos p/3 - 2sin p/3 =-1-3½.
15.
On note Re(z) la partie réelle et Im(z) la partie imaginaire d’un
nombre complexe z.
Si z1 et z2 désignent deux nombres complexes non
nuls, alors Re ((z1 +iz2) (1+i)) est égale à :
a. Re (z1
−z2)−Im(z1 +z2) ; vrai.
b. Re (z1)−Im(z2)
;
c. Re (z1
−z2) ;
d. Im(z1)−Re
(z2).
a, b, c et d réels ; z1 = a+ib ; z2 = c+id ; iz2
= -d +ic ; z1 +iz2 =(a-d)
+i(b+c) ;
(z1 +iz2) (1+i) =(a-d) +i(b+c) +i[(a-d) +i(b+c)]=a-d -b-c +i(b+c+a-d).
Partie réelle : a-c-(b+d) = Re(z1 −z2) -Im(z1 +z2).
16. Si z = cos p/8
+ i sni p/8 ,
alors z8 est égal à :
a. 1 ; b. i ; c. −1
vrai ; d. −i.
z = exp(ip/8)
; z8 =exp(i 8p/8)=exp(ip) =cos p + i sin p = -1
17.
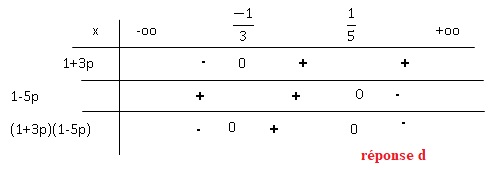
Soit p un nombre réel et (E) l’équation suivante :
2pz2 +(1−p)z +2p = 0.
À quel ensemble doit appartenir p pour que (E) ait deux racines
complexes conjuguées distinctes ?
Le discriminant doit être négatif :(1-p)2 -16p2
< 0.
(1-p+4p)(1-p-4p) < 0 ; (1+3p)(1-5p) < 0.
18. Soient z1
et z2 deux nombres complexes d’arguments respectifs :
arg (z1)=5p
/8 et arg (z2) =5p
/6 dans ]−p ; p]..
On peut alors affirmer que la valeur dans ]−p ; p] de arg(z1 ×z32)
est :
arg(z1 ×z32)
=5p
/8 +15p
/6 =5p
/8 +5p
/ 2 =5p
/8 +20p
/ 8 =25p
/ 8 =4 p-7p/8. Réponse b.
19. Dans le plan
complexe, on appelle A le point d’affixe (−2+3i) et I le point d’affixe
(5+6i).
Le symétrique A' de A par rapport à I a pour affixe :
a. −9−2i ;
I milieu de AA' ; 5 =(-2 +xA') / 2 ; xA' =12 ; 6 =(3 +yA') / 2 ; yA' =9.
b.
−3+ 5,5 i
c. −9+13i ;
d. 12+9i. Vrai.
20. Dans le plan
complexe, on considère trois points distincts A, B, C d’affixes
respectives zA, zB, zC avec :
AB= 8 cm et( zC −zA) / (zB −zA
)=0,75 i.
La longueur du segment [BC] est égale à :
a. 6 cm ; b. 8 cm ; c. 9 cm ; d. 10
cm. Vrai.
zC-zB =zC-zA +zA-zB
=0,75 i(zB −zA ) +zA-zB =(zB −zA )(-1+0,75 i)
Module de -1 +0,75i = (1+9 /16)½ =5 / 4.
BC = 5 /4 AB =5 / 4 x8 = 10 cm.
|
|
Fonctions.
21. Dans le plan muni d’un repère
orthonormé, on note D
la droite d’équation y = x.
Par ailleurs, pour n ∈N, on note (Cn) la courbe
représentative de la fonction définie par : f(x) =x2 +nx +1
Combien existe-t-il d’entier(s) naturel(s) n pour le(s)quel(s) (Cn)
et D n’ont aucun point en commun ?
a. 1 ; b. 2 ; c. 3 ; d. une
infinité. Vrai.
x2 +nx
+1 doit être différent de x soit x2 +(n-1)x +1 non nul.
x2
+(n-1)x +1=0 ; discriminant : (n-1)2-4 =0 ; n-1 =± 2 ; n =3
et n = -1 ( exclu).
n doit être différent de 3.
22. La limite, lorsque x tend vers 2
de (x2-x-2) / (x2-3x-2) est égale à :
a. 0 vrai ; b. +oo ; c. 2 ; d. 3.
Le dénominateur tend vers -4 et le numérateur tend vers zéro.
23. Le domaine de
définition de la fonction f, définie par :
f (x) = lnx / [(ln(x-3½) +ln(x+3½)].
x >0 et x-3½ > 0 soit x > 3½
et x+3½ > 0
soit x > -3½ .
x doit être
supérieur à 3½.
Le dénominateur ne doit pas être nul :
(ln(x-3½)
+ln(x+3½) = ln[x-3½)(x+3½)] =ln(x2-3)
différent de zéro soit x2-3 différent de 1 ; x différent de
±2
]3½ ; 2 [ union ]2 ; +oo[. Réponse
d.
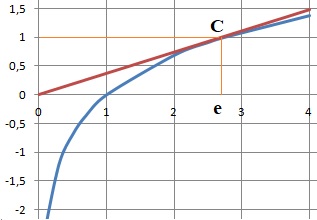
24. Dans le plan
muni d’un repère orthonormé, on note C la courbe représentative de la
fonction définie par f(x)= ln(x). L’ordonnée du point de C en lequel la
tangente à C passe par l’origine du repère est égale à :
a. 0 ; b. 1 vrai ; c. e ; d. −1.
Dérivée f '(x) = 1 /x. Coefficient directeur de la tangente à la courbe
au point C : 1 /xC.
Equation de la tangente à la courbe au point C passant par l'origine y = xC /
/xC =1.
25. Le domaine de
définition de la fonction f , définie par :
f (x) = ln(3x +2xex −xe2x ) est :
a. ]ln3 ; +∞[ ; b. ]−∞; 0[∪] ln3 ; +∞[ ; c. ]0 ; +∞[ ; d. ]0 ; ln3[ vrai.
3x +2xex
−xe2x > 0 ; x(3 +2ex-e2x) > 0 ;
Etude du signe
de 3 +2ex-e2x
en pose X = ex
positif ; 3 +2X-X2 =0.
Discriminant : 4 +12 = 16 ; solutions X1 =(-2 +4) / (-2) =
-1 (exclu) et X2 = +3 ;
x =ln(3) ; 3 +2X-X2
est positif sur ]0 ; 3[ ; 3
+2ex-e2x est positif sur ]0 ; ln(3) [.
26. Soit f la
fonction définie par f (x) = ln(ln(x½)). En notant f ′ la
fonction dérivée de f , on peut affirmer que l’expression de f ′(x) est
:
a. 1 /(x ln(x)) vrai ; b. 1 / ln(x½) ; c. 1/(x ln(x½)) ; d. 1
/(x ln(ln(x))).
On pose u = ln(x½) =0,5 ln(x) ; u' = 0,5 / x ; f '(x) = u' /
u = 0,5 / (x ln(x½)) = 0,5 /(0,5x ln(x)) = 1 /(x ln(x)).
27. Soit f la
fonction définie par f (x) = ln(x2 −9x −22). La limite de f
(x), lorsque x tend vers 11 par valeurs supérieures, est égale à :
a. 0+ ;
b. 0− ; c. −∞ vrai ; d. +∞.
Quand x tend vers
11+ : x2 −9x −22 tend vers 0+ ; ln(x2 −9x −22) tend vers moins
l'infini.
28. Dans
l’ensemble des nombres réels, l’équation e2x −1 = 6e−2x
admet :
a. aucune solution ;
b. une solution
strictement supérieure à ln(2½) ; vrai
c. une solution
strictement inférieure à ln(2½)
;
d. deux solutions
de signes contraires.
On pose X = e2x positif ; X-1 = 6 /X ; X2 -X-6=0
; discriminant : 25 ; solution retenue X =3 soit ln(3) = 2x ; x = 0,5 ln(3)~0,55.
Or ln(2½) ~0,35.
29. Soit f la
fonction définie sur R par f (x) = e2x +ex .
Dans le plan muni d’un repère orthonormé, on note (C ) la courbe
représentative de f et D
la droite d’équation y = x.
Combien (C ) possède-t-elle de tangente(s) parallèle(s) à D ?
a. 0 ; b. 1 vrai ; c. 2 ; d. 4.
Coefficient directeur des tangentes à la courbe C : f '(x) = 2e2x+ex.
Ces tangentes sont parallèles à la droite d'équation y = x.
2e2x+ex=
1 ; 2e2x+ex
-1 = 0.
On pose X = ex positif ; 2X2 +X-1 = 0 ;
discriminant : 9 ; solution retenue : X =0,5 ; x = ln(0,5).
30. Soit f la fonction définie sur R
par f (x) =(e2x-3) / (ex+1).
Dans le plan muni d’un repère orthonormé, combien la courbe
représentative de f possède-telle de tangente(s) parallèle(s) à l’axe
des abscisses ?
a. 0 vrai ; b. 1 ; c. 2 ; d. 3.
Calcul de f '(x) en posant u = e2x-3 et v = ex+1
; u' = 2e2x ; v' = ex ; f '(x) =[ 2e2x(ex+1) -ex(e2x-3)] / (ex+1)2.
f '(x) =(e3x+2e2x+3ex)
/ (ex+1)2
= ex(e2x+2ex +3) /
(ex+1)2 .
Coefficient directeur d'une tangente parallèle à l'axe des
abscisses : zéro.
e2x+2ex
+3 = 0 ; on pose X = ex ; X2 +2X+3=0 ;
discriminant négatif, aucune solution réelle.
31. Dans le plan
muni d’un repère orthonormé, on note (C ) la courbe représentative de f
, définie sur R, par f (x) = exp(x2+x+1).
Combien (C ) possède-t-elle de tangente(s) passant par l’origine ?
a. 0 ; b. 1 ; c. 2 vrai ; d. 4.
Calcul de la dérivée en posant X =x2+x+1 ; X' = 2x+1 ; f
'(x) = (2x+1)exp (x2+x+1).
Equation d'une tangente à la courbe passant par l'origine : y = f '(x) x .
Au point de tangence : exp(x2+x+1)
=(2x+1)exp (x2+x+1) x.
(2x+1)x =1 ; 2x2 +x-1 = 0 ; solutions -1 et +0,5.
32. Soit u une
fonction définie et dérivable sur R et à valeurs non nulles.
On définit f la fonction inverse de u par f =1 /u
Sachant que l’équation de la tangente à la courbe représentative
de u au point d’abscisse x = −2 est y = 2x + 3, on peut affirmer que f
′(−2) est égal à :
a. −2 vrai ; b. −1 ; c. 1 ; d. 2.
u'(-2) = 2 ; f ' = -u'/u2 ; f '(-2) = -u'(-2) / u(-2)2
= -2 /u(-2)2 avec u(-2) = 2(-2)+3) =-1.
|
|
33.
Soit f une fonction définie et dérivable sur R, on note f ′ sa fonction
dérivée. Dans le plan muni d’un repère orthonormé, la courbe
représentative de f est symétrique par rapport à l’origine.
Sachant que la limite en plus l'infini de f '(x) est égale à 2019 , on
peut affirmer que :
a. la limite en
moins l'infini de f '(x) est égale à 2019 ,
b. la limite en
moins l'infini de f '(x) est égale à -2019 , vrai
c. la limite en
moins l'infini de f '(x) est égale à zéro ,
d. la limite en
moins l'infini de f '(x) est égale à 1.
34. Quelle est la
valeur du nombre réel a tel
que :
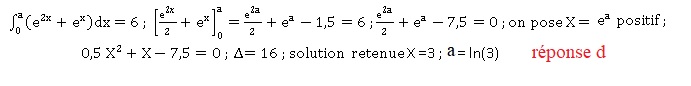
Pour les questions 36 à 50, on considère une fonction u définie et
dérivable sur R, dont la représentation graphique dans le plan muni
d’un repère orthonormé est donnée ci-après :
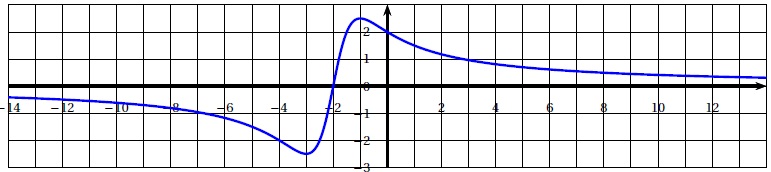
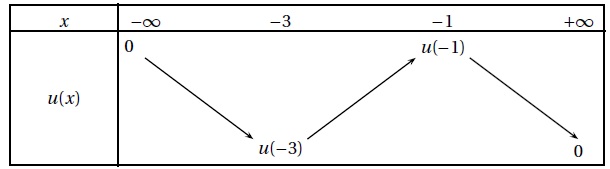
On donne de plus le tableau de variation de u :
36. On peut
affirmer que l’image de 8 par la fonction u est :
a. strictement
supérieure à 5;
b. strictement
inférieure à 5; vrai
c. égale à 5;
d. aucune des trois
affirmations précédentes n’est correcte.
37. La limite,
lorsque x tend vers +∞, de u(x) est égale à :
a. +∞ ; b. −∞ ; c. 0 vrai ; d. 1.
38. Combien la
valeur 0 a-t-elle d’antécédent(s) par la fonction u ?
a. 0 ; b. 1 vrai ; c. 2 ; d. une infinité.
u(-2) =0.
39. Parmi les
tableaux de signes suivants, lequel correspond à la fonction u ?

40. Parmi les
tableaux de signe suivants, lequel correspond à la fonction u′ ?

Pour les questions 41 à 45, on suppose que u est la fonction dérivée
d’une fonction f définie et dérivable sur R.
Par ailleurs, on suppose le plan muni d’un repère orthonormé et on note
(C ) la courbe représentative de f .
41. Sachant que f
(10) = 12, on peut affirmer que :
a. f (11) = 12 ; b. f (11) > 12 vrai ; c. f (11) < 12 ; d. on ne peut rien affirmer
concernant f (11).
Pour x > 10, u est positive ; f(x) est donc croissante.
42. Combien (C )
possède-t-elle de tangente(s) horizontale(s) ?
a. 0 ; b. 1 vrai ; c. 2 ; d. une infinité.
La tangente à la courbe C est horizontale lorsque f '(x) = u(x) = 0.
43. Que vaut f(2)
sachant que :
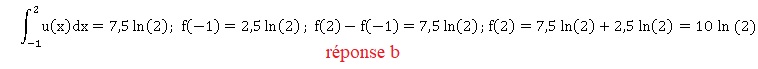
44. Parmi les
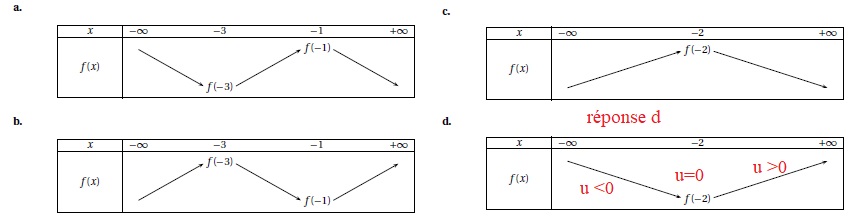
tableaux de variation suivants, lequel correspond à la fonction f ?
45. On dit qu’une
fonction dérivable h est convexe (respectivement concave) sur un
intervalle I si h′ est croissante (respectivement décroissante) sur I.
Si h est convexe sur [a ; b] et concave sur [b ; c] (avec a < b <
c) ou si h est concave sur [a ; b] et convexe sur [b ; c], alors le
point de la courbe représentative de h d’abscisse b est qualifié de
point d’inflexion.
Combien la courbe représentative de f possède-t-elle de points
d’inflexion?
a. 0 ; b. 1 ; c. 2 vrai ; d. 3.
u décroît sur ]-oo ; -3[ ; f est concave sur cet intervale.
u croît sur ]-3 ; -1 [ , f est convexe sur cet intervalle.
u décroît sur ]-1 ; +oo[ ; f est concave
sur cet intervale.
La concavité change aux points d'abscisses -3 et -1.
Pour les questions 46 à 50, on note g la fonction dérivée de u.
46. Sachant que g
(0) = −0,6, on peut affirmer que :
a. g (1) = −0,6 ; b. g (1)> −0,6 ; c. g (1) < −0,6 ; d. on ne peut rien affirmer
concernant g (1). vrai.
u décroît sur ]-oo ; -3[ ; g est négative
sur cet intervale.
u croît sur ]-3 ; -1 [ , g est positive sur cet intervalle.
u décroît sur ]-1 ; +oo[ ; g est négatve
sur cet intervale ; de plus g(0) = -0,6.
47. Parmi les
tableaux de signe suivants, lequel correspond à la fonction g ?
Erreur d'énoncé, les 4
tableaux proposés sont indentiques et faux.
48. On peut
affirmer que :
a. g (x) n’admet
pas de limite lorsque x tend vers +∞;
b. g (x) tend vers
+∞lorsque x tend vers +∞; faux,
g(x) < 0 sur ]-1 ; +oo[
c.
g (x) tend vers −∞lorsque x tend vers +∞;
d. g (x) admet une
limite finie lorsque x tend vers +∞. vrai.
u tend vers zéro lorsque x tend vers plus l'infini.
En plus l'infini, le coefficient directeur de la tangente à la courbe
tend vers zéro.
49. L'intégrale
suivante est égale à :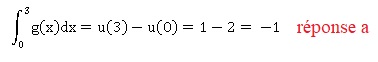
50. Soit G la
primitive de g sur R définie sur R par :G(x) =(5x+10) / (x2+4x+5)
+2019. On a alors :
a. u(x) =5(x+2) / (x2+4x+5)
+2019.
b.
u(x) =5(x+2) / (x2+4x+5).
c.
u(x) =[5(x2+4x+5)-(5x+10)(2x+4)]
/ (x2+4x+5)2. Vrai.
d. aucune des
affirmations précédentes n’est correcte.
On dérive G en posant u = 5x+10 et v = x2+4x+5
; u' = 5 ; v' = 2x+4.
(u'v -v'u) / v2 = u(x) =[5(x2+4x+5)-(5x+10)(2x+4)]
/ (x2+4x+5)2.
Trigonométrie.
51. Dans le plan
muni d’un repère orthonormé, on considère les points du cercle
trigonométrique A et B de coordonnées respectives :
cos(2p/3) ; sin(2p/3) et cos(11p/6) ; sin(11p/6).
Les coordonnées du milieu du segment [AB]
sont :
a. nulles ; b. opposées ; c. égales vrai ; d. inverses l’une de l’autre.
½[cos(2p/3) +cos(11p/6)]=cos[½ (2p/3 + 11p/6)] cos[ ½(2p/3 - 11p/6)]=cos(5p/4)cos(-7p/12).
½[sin(2p/3) +sin(11p/6)]=sin[½ (2p/3 + 11p/6)] cos[ ½(2p/3 - 11p/6)]=sin(5p/4)cos(-7p/12).
Avec cos(5p/4) = sin(5p/4).
52.
Parmi les formules suivantes une seule est correcte. Laquelle ?
a. cos(cos(2a))=
cos((cosa)2)sin((sina)2)+sin((cosa)2)cos((sina)2);
b. cos(cos(2a))=
cos((cosa)2)sin((sina)2)sin((cosa)2)cos
((sina)2);
c. cos(cos(2a)) =
cos((cosa)2)cos ((sina)2)+sin((cosa)2(sin((sina)2);
vrai
d. cos(cos(2a)) =
cos ((cosa)2)cos((sina)2)−sin((cosa)2)sin((sina)2).
cos(2a) =cos2a-sin2a.
cos(cosa) = cos[cos2a-sin2a] =cos (A-B)
avec A = cos2a et B =sin2a.
cos (A-B) =cos A cos B +sinA sin B.
53.
Combien de solutions appartenant à l’intervalle ]-p/2 ; p/2[ l’équation
2(sinx)2 +3cos x = 3 possède-t-elle?
a. 0 ; b. 1 ; c. 2 ; d. 3. Vrai.
sin2x = 1-cos2x ; 2-2cos2x+3cos x = 3 ; 2cos2x-3cos x +1=0.
On pose X = cos x avec -1 <
X< 1 ; 2X2
-3X +1 = 0 ; discriminant :1 ; solutions retenues : 0,5 et 1 ;
cos x = 1 ; x = 0 ; cos x = 0,5 ; x =±p/3.
Probabilités.
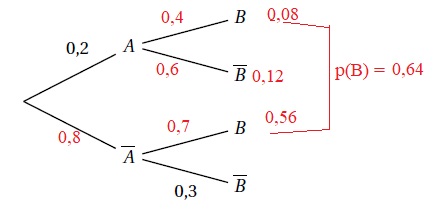
54 On considère l’arbre de
probabilité suivant :
Sachant
que P(B) = 0,64, que vaut P(A∩ non B)?
a. 0,12 vrai ; b. 0,08 ; c. 0,16 ; d. 0,42.
55. Une première
urne U1 contient k boules rouges et 2k +1 boules bleues,
avec k entier naturel non nul.
Une deuxième urne U2 contient 4 boules rouges et 5 boules
bleues. Le jeu consiste à tirer aléatoirement une boule dans U1
puis de la verser dans U2 avant d’effectuer un deuxième
tirage aléatoire d’une boule dans U2.
On appelle R l’évènement « obtenir une boule rouge à l’issue du
deuxième tirage ».
Sachant que p(R) = 0,43, quelle est l’affirmation exacte parmi les
quatre suivantes ?
a. k divise k2
−2 ; b. k divise 12 vrai ; c. k divise 10 ; d. k divise k2 −4.
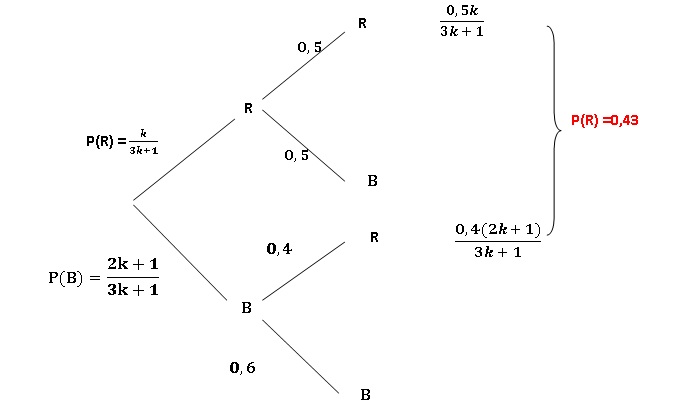
0,5 k +0,8k +0,4 = 0,43(3k+1) ; 0,01 k = 0,03 ; k = 3.
56. Soient A et B
deux évènements indépendants tels que :P(A∩B) = 0,32 et P(B) = 2P(A).
La probabilité de l’évènement B est égale à :
a. 0,04 ; b. 0,08 ; c. 0,16 ; d. 0,8 vrai.
P(A) x P(B) =0,32 ; P(A) x2 P(A) = 0,32 ; P(A)2 = 0,16 ;
P(A) =0,4 ; p(B) = 0,8.
57. Soit X une
variable aléatoire suivant la loi binomiale de paramètres 2 et p.
Sachant que p < 0,5 et que V (X) = 128 (où V (X) désigne la variance
de X), on peut affirmer que :
a. p = 0,05 ; b. p = 0,1 ; c. p = 0,2 ; d. p = 0,25.
erreur dans le texte n =
2 , si on prend n = 800 :
V = n p(1-p) =2p(1-p) =128 ; p(1-p) = 0,16 ; p2-p+0,16 = 0.
Discriminant : 0,36 ; solution retenue p =0,2.
58. Soit X une
variable aléatoire suivant la loi binomiale de paramètres 2 et p, où p
∈ [0 ; 1]. Sachant que p(X = 1) =0,5, on peut affirmer que le réel p
est égal à : a. 0 ; b. 0,25 ; c. 0,5 vrai ; d .
1.
p(X) = 2 p(1-p)=0,5 ; p(1-p) = 0,25 ; -p2 +p=0,25 ; p2-p+0,25=0
; p = 0,5.
Géométrie dans l'espace.
59. On suppose
l’espace muni d’un repère orthonormé. Soit (P) le plan dont une
équation paramétrique est :
x = 2+t +t ′
y = −2t +3t ′
z = −2+t −5t ′
avect ∈ R et t ′ ∈ R
Parmi les points suivants, lequel n’appartient pas à (P) ?
a. A(2 ; −5 ; 0) vrai ; b. B(4 ; 1 ; −6) ; c. C(2 ; 0 ; −2) ; d. D(3 ; −7 ; 5).
Si A appartient à (P) : 2 = 2 +t +t' soit t' = -t.
-5 = -2t +3t' = -5t ; t = 1 ; t' = -1.
0 diffère de -2 +t-5t' =4 ; A n'appartient pas au plan.
Si B appartient à
(P) : 4 = 2 +t +t' soit t+t' = 2 ou t' = 2-t.
1 = -2t +3t' = -2t +6-3t ; t = 1 ; t' = 1.
-6 = -2 +t-5t' ; B appartient au plan.
Si C appartient au plan : 2 =
2 +t +t' soit t+t' = 0 ou t' = -t.
0 = -2t +3t' = -2t -3t ; t = 0 ; t' = 0.
-2 = -2 +0+0 ; C appartient au plan.
Si D appartient à (P) : 3 = 2 +t +t' soit
t+t' = 1 ou t' = 1-t.
-7 = -2t +3t' = -2t +3-3t ; t = 2 ; t' = -1.
5= -2 +t-5t' =-2+2+5 ; D appartient au plan.
60. On suppose
l’espace muni d’un repère orthonormé. Soient A(1; 2; 3) et B(3; 2; 1).
L’ensemble des points de l’espace équidistants de A et de B est :
a. uniquement
constitué du point 1 (2; 2; 2) ;
b. une droite
passant par le point 1(2; 2; 2) ;
c. le cercle de
centre (2; 2; 2) et de diamètre 0,5 AB;
d. un
plan passant par le point I(2; 2; 2). Vrai.
|
|