Physique chimie,
Concours interne TSPEI 2018.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
|
Préparation du titane.
Le titane est obtenu en faisant réagir le dioxyde de titane TiO2 avec du chlorure de calium CaCl2
en fusion dans un creuset en carbone avec une électrode en carbone. Par
application d'une tension, le chlorure de calcium se transforme en
calcium qui réagit avec le dioxyde de titane pour former le titane et
l'oxyde de calcium CaO.
1.
Donner la structure électronique du titane et de l'oxygènz. Z(Ti) = 22
; Z(O) = 8. Quels sont les ions susceptibles de former le titane et
l'oxygène ?.
Ti : 1s2 2s2 2p6 3s2 3p6 4s2 3d2.
O : 1s2 2s2 2p4 .
Le titane peut donner des ions Ti2+ et Ti4+ ; l'oxygène donne l'ion O2-.
2.
Les électronégativités du titane et de l'oxygène sont respectivement de
1,5 et 3,5. Caractériser la liaison interatomique dans l'oxyde.
La liaison est polarisée, l'oxygène portant une charge partielle négative et le titane une charge partielle positive.
3. Ecrire l'équation de la réaction entre le calcium et l'oxyde de titane.
2Ca + TiO2 ---> 2 CaO + Ti.
4. Montrer en utilisant les nombre d'oxydation que cette réaction est une réduction.
Le nombre d'oxydation du titane passe de +IV dans TiO2 à zéro dans Ti.
Le nombre d'oxydation du calcium passe de zéro dans Ca à +II dans CaO.
TiO2 est réduit par le calcium.
5. Quelle masse de dioxyde de titane m(TiO2) doit-on utiliser pour préparer 1,00 kg de titane ?
M(Ti) = 47,9 g / mol ; M(Ca) = 40,1 g/mol.
Quantité de matière de titane : n = 1,00 103 47,9 =20,877 mol.
Quantité de matière de dioxyde de titane : n = 20,877 mol.
M(TiO2) = 47,9 +2 x16 = 79,9 g / mol.
m(TiO2) =79,9 x20,877 ~ 1,67 103 g = 1,67 kg.
6. Quelle masse de cclcium m(Ca) doit-on produire dans le creuset pour préparer le titane ?
Quantité de matière de calcium : 2 n = 2 x20,877 = 41,754 mol.
m'Ca) = 40,1 x41,754 ~1,67 103 g = 1,67 kg.
Accumulateur Ni-Cd.
1. Ecrire les deux
demi-équations électroniques correspondant aux deux couples
oxydants-réducteurs intervenant dans l'accumulateur.
Couple Cd(OH)2 / Cd : E°2 = -0,81 V.
Cd + 2HO- =Cd(OH)2 +2e-. Oxydation.
NiO (OH) / Ni(OH)2 : E°1 =+0,49 V.
NiO(OH) +e- +H2O = Ni(OH)2+ HO-. réduction.
2. Quel est l'oxydant le plus fort ? Le réducteur le plus fort ?
Le réducteur le plus fort est Cd ; l'oxydant le plus fort est NiO(OH).
3. Donner la polarité de l'accumulateur.
Cd + 2HO- =Cd(OH)2 +2e-. Oxydation.
Le cadmium est la borne négative de l'accumulateur.
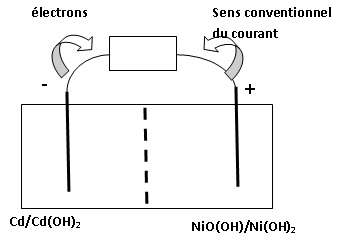
4. Faire le schéma
électrique de l'accumulateur associé à un conducteur ohmique en
précisant le sens de déplacement des électrons et le sens conventionnel
du courant.
5. Montrer que l'équation de la réaction de fonctionnement s'écrit :
2 NiO(OH) + Cd + 2H2O --> 2Ni(OH)2 +Cd(OH)2.
Cd + 2HO- =Cd(OH)2 +2e-.
2NiO(OH) +2e- +2H2O = 2Ni(OH)2+2 HO-.
Ajouter et simplifier.
2NiO(OH) +2e- +2H2O +Cd + 2HO- ---> 2Ni(OH)2+2 HO-+Cd(OH)2 +2e-.
2 NiO(OH) + Cd + 2H2O --> 2Ni(OH)2 +Cd(OH)2.
Cet accumulateur contient m(Cd) = 500 g de cadmium.
6. Calculer la quantité de matière de cadmium correspondante. m(Cd) = 112,4 g / mol.
n = 500 / 112,4 =4,4484 ~4,45 mol.
7. En déduire la
quantité de matière d'électron circulant lors du fonctionnement ainsi
que la charge Q théorique que l'accumulateur est capable de fournir.
n(e-) = 2 n = 8,897 ~8,90 mol.
Q = n(e-) F = 8,897 x9,65 104 = 8,59 105 C.
|
|
|
Extraction d'huiles végétales.
L'huile de soja est extraite à partir de graines par solvant. On fait couler en continu de l'hexane C6H14
sur le produit à extraire, l'hexane se charge en huile. 1,5 L d'hexane
permet d'extraire 1,0 kg d'huile. Le mélange hexane huile est séparé
par distillation à 70 °C. Les vapeurs sont condensées et le liquide
récupéré est décanté pour séparer l'eau de l'hexane.
1. Donner la formule développée, la formule semi-développée ainsi que l'écriture topologique de la molécule d'hexane.
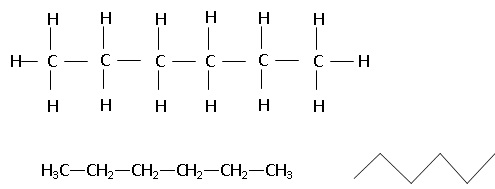
2. Justifier que la molécule d'hexane soit apolaire et le choix d'un solvant apolaire pour l'extraction.
C et H ont des électronégativités proches. Du fait de sa symétrie, la molécule d'hexane est apolaire.
L'hexane et l'huile de soja apolaire ont des affinités.
3. La masse
molaire de l'hexane est M = 86,0 g / mol et sa densité d = 0,66.
Calculer la masse m puis la quantité de matière n d'hexane dans un
volume V = 1,5 L d'hexane.
Masse d'hexane : m = 1,5 x 0,66 = 0,99 kg.
n = 990 / 86,0 = 11,511 ~11,5 mol.
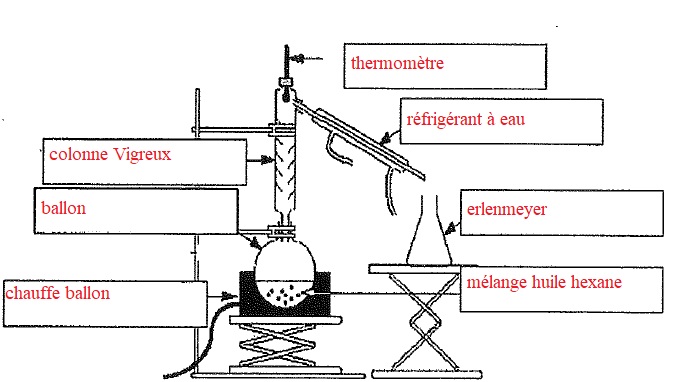
4. La distillation fractionnée s'effectue à l'aide du dispositif suivant. Annoter ce schéma.
5. La décantation
s'effectue dans une ampoule à décanter. La représenter et y faire
apparaître, en justifiant brièvement, les deux phases.
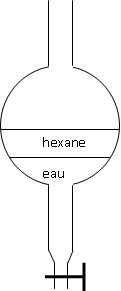
Dans l'ampoule à décanter, le solvant le plus dense ( l'eau ) occupe la partie inférieure.
|
|
|
|
Surveillance par drone.
L'appareil photographique embarqué sur le drone est modélisé par :
un objectif constitué d'une lentille mince L de distance focale f ' = 40 mm ;
un diaphragme circulaire de diamère D ;
un capteur photosensible CCD 6,17 x 4,62 mm sur lequel se forme l'image..
1. La lentille est-elle convergente ou divergente ? Justifier.
Une lentille convergente possède une distance focale positive.
2. Faire un schéma de l'appareil photographique modélisé.
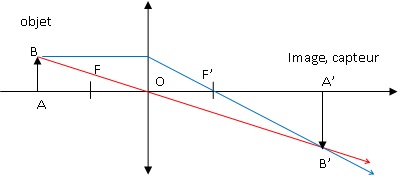
3. A quoi correspondent les indications 6,17 x 4,62 mm du capteur.
Ce sont les dimensions du capteur.
Le drone est immobile à une altitude de 150 m. L'appareil photo est
positionné sous le drone. On supposera que son plan reste parallèle à
la surface du sol et que l'altitude est grande devant les hauteurs des
bâtiments situés sur la parcelle de terrain photographié.
4. Rappeler les formules de conjugaison et de grandissement de Descartes.
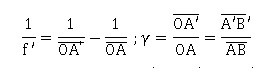
5. A quelle
distance de l'objectif se forme l'image de la parcelle ? L'objet est
considéré à l'infini ; l'image se forme dans le plan focale image de la
lentille . OA' = f ' = 40 mm.
6. Faire un schéma , sans souci d'échelle, faisant apparaître la parcelle, la lentille L, son centre optique O et le capteur CCD.
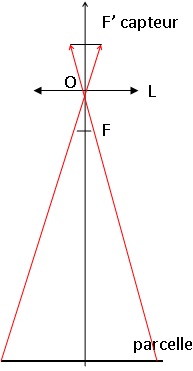
7. Quelle est la taille de la parcelle qui peut être photographiée ?
|1 / g| =150 / 0,04 =3750.
3750 x 6,17 10-3 ~23,3 m ; 3750 x 4,12 10-3 ~15,5 m.
Plate forme pétrolière.
On s'intéresse au remorquage d'une plate forme flottante. La plate
forme est assimilée à un parallélépipède de hauteur h, de largeur l, de longueur L et de masse volumique r. la plate forme est immobile à la surface de l'eau de masse volumique re. On appelle a la hauteur à l'air libre.
1. Faire le bilan des forces s'exerçant sur la plate forme.
La plate forme est soumise à son poids, verticale vers le bas, P = mg
et à la poussée d'Archimède, verticale vers le haut , valuer = poids du
volume d'eau déplacé.
2. Exprimer ces forces en fonction des données.
Volume de la plate forme : V = L l h.
Masse correspondante m = r V = r L l h.
Poids P = r L l h g.
Volume immergé V' = L l (h - a).
Masse d'eau déplacé : re L l (h-a).
Poussée : P = re L l (h-a).g.
3. Exprimer le rapport a / h en fonction de r et re.
A l'équilibre P = F ; r L l h g = re L l (h-a) g.
r h = re (h-a) ; (h-a) / h = r / re ; 1-a / h = r / re ; a / h =1- r / re .
Le remorqueur déplace la plate forme de masse m à la vitesse v selon
une trajjectoire rectiligne sous l'action d'une force de traction F On
fait l'hypothèse que les forces de frottements sont modélisées par une
expression du type f =av avec a positif.
4. Faire le bilan des forces s'exerçant sur la plate forme.
Poids, poussée d'Archimède opposée au poids, force motrice et frottements.
5. Etablir l'équation différentielle du mouvement.
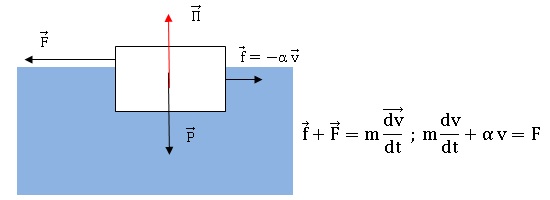
6. Résoudre cette équation et montrer que la solution peut se mettre sous la forme :
v(t) = vL (1-e-t / t).
dv /dt +a / m v = F / m. (E). On pose t = m / a. Constante de temps.
Solution générale de dv/dt + v / t = 0 : v(t) = A e-t / t avec A une constante.
Solution particulière de (E) : vL = F / a, vitesse limite.
Solution générale de (E) : v(t) = A e-t / t + vL.
La vitesse initiale est nulle : 0 = A + vL ; A = -vL.
Par suite : v(t) = vL (1-e-t / t).
|
|
|
|
Capteur d'humidité.
Un capteur d'humidité a pour résistance R = A e-Bh où h est l'humidité relative ( h = 0,5 pour une humidité de 50 %), A = 6,92 1012 et B = 21 des constantes. Il est branché en dérivation avec une résistance R' = 1 MW.
1. Quelle est l'unité de A dans le systàme internationnal ?
e-Bh est sans unité, donc A a la dimension d'une résistance ( ohm).
2. Donner l'expression de la résistance R1 correspondant à l'association des deux résistances R et R'.
R1 = R R' / (R+R').
3. Calculer les valeurs de R et R1 pour h = 0;5.
R = 6,92 1012 exp(-21 x0,5) = 1,9055 108 ohm = 190,55 MW~191 MW.
R1 = 190,55 /191,55 =0,995 MW.
La résistance R1 est placée dans un pont de Wheastone. R3 = R4 = 10 kW.
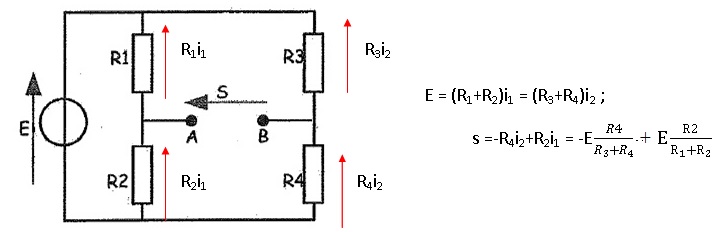
4. Montrer que la tension s =uAB peut se mettre sous la forme : s = E[R2 / (R1+R2) - R4 / (R3+R4) ].
5. Le pont est à l'équilibre si s = 0. En déduire la valeur de R2.
R2 / (R1+R2) = R4 / (R3+R4) = 0,5 car R3 = R4 .
R2 = 0,5 (R1+R2) ; R1=R2 =0,995 MW.
|
|