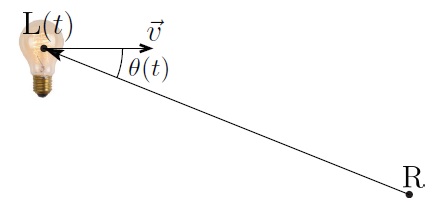Applications
de l'effet Doppler, Expérience de
Ives-Stilwell,
Concours général physique 2019.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
......
.....
|
|
I. A.
Explication théorique de l'effet Doppler.
1. Une lampe se déplace
horizontalement à la vitesse v, en émettant des flashs. La périodicité
des flash est notée Tl.
La vitesse de la lampe se détermine en étudiant le déplacement du
centre des surfaces d'onde.
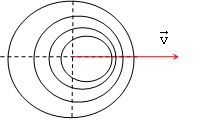
2. La
distance initiale entre l'émetteur ( la lampe ) et le récepteur est
notée RL(0). La lumière se déplace dans l'air à la célérité c.
Le premier flash est perçu par le récepteur à la date t1 =
RL(0) / c.
3. A la date
t=Tl le second flash est émis.
La distance entre émetteur et récepteur est TL(Tl).
Le second flash parvient au récepteur à la date t2 = Tl
+TL(Tl) / c.
4. L'émetteur
( lampe) se déplaçant à la vitesse v en direction du récepteur fixe :
TL(Tl)= TL(0) - v Tl.
5. La durée
séparant la réception de deux flashs successifs est TR = t2-t1.
TR = Tl +TL(Tl) / c -RL(0)
/ c.
TR = Tl -v / c Tl= Tl ( 1-v / c).
Or la vitesse de la lampe est inférieure à la célérité de la
lumière dans l'air.
v < c, TR < TL.
6. Lorsque la
lampe s'éloigne du récepteur TR = Tl ( 1+v / c).
TR > TL.
7.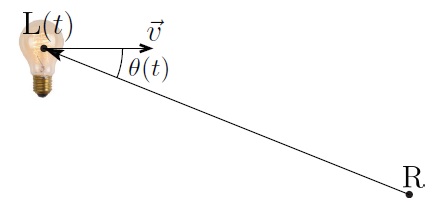
Dans ce
cas TR = Tl ( 1-v / c cos q).
Pour la question 5, q
= 0 et TR = Tl ( 1-v / c).
Pour la
question 6, q = p et TR = Tl ( 1+v / c).
8. Expression
de la longueur d'onde mesurée au niveau du récepteur l = c TR.
Longueur d'onde émise : l
l= c Tl.
La lampe se rapproche du récepteur : Dl- = l-ll = c [Tl ( 1-v / c)- Tl ]= -v Tl
= - v / c ll.
La lampe
s'éloigne du récepteur : Dl+ =
l-ll = c [Tl ( 1+v / c)- Tl ]= v Tl
= v / c ll.
Application à
l'étude du satellite LO-19.
Les figures a et b représentent les fréquences des ondes provenant de
LO-19, en fonction du temps, lors de deux passages successifs le 22
août 1991.
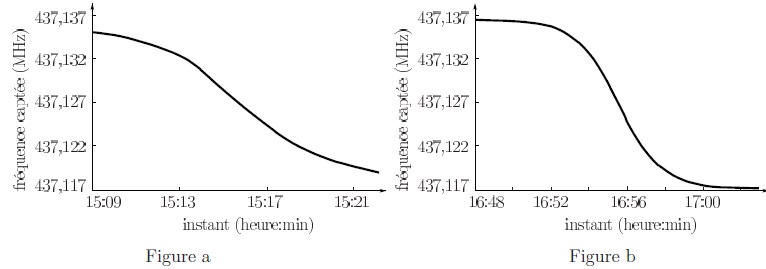
9. Expliquer
qualitativement la variation de la courbe sur la figure b entre 16h48
et (environ) 16h52 d’une part, puis entre (environ) 17h00 et 17h03
d’autre part.
L'orbite
du satellite est circulaire, sa vitesse est donc constante.
De plus les fréquences captées sont constantes.
Dans l'hypothèse où le satellite est à basse altitude, l'angle q est constant.
Pour la courbe entre 16h 48 et 16 h 52, on se trouve dans le cas où q = 0 ( question 5).
Pour la courbe
entre 17h 00 et 17 h 03, on se trouve dans le cas où q = p ( question 6).
10. Au contraire, comment interpréter la variation de la courbe entre 16h54 et 16h57 ?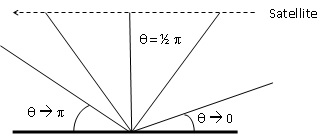
Approche du satellite entre 16 h 54 et 16 h 57 :
q
varie de zéro à 90°.
TR croît et la fréquence reçue = 1 / TR, diminue
pour atteindre la fréquence d'émission ( satellite à la verticale de la
balise terrestre ).
Lors de
l'éloignement du satellite : q
varie de 90° à 180°.
TR croît et la fréquence reçue = 1 / TR, diminue.
11. Estimer le plus précisément possible la fréquence à laquelle les ondes sont émises par LO-19.
Du fait
de la symétrie du mouvement, la vitesse d'approche est identique à la
vitesse d'éloignement.
La fréquence d'émission est égale à : ( fréquence d'approche +
fréquence d'éloignement ) / 2 = (437,137 +437,117) / 2 = 437,127 MHz.
12. Estimer la période du satellite sur son orbite. On détaillera la méthode, ainsi que les hypothèses formulées.
La
période du satellite est égale à la durée séparant deux réceptions
successives à la même fréquence.
Le récepteur reçoit la fréquence de 437,127 MHz à 15 h 15 et à 16 h 55.
Période orbitale du satellite : 16 h 55 -15 h 15 = 1 h 40 min ou 100
min ou 6,0 103 s.
13. Déduire de la question précédente le rayon de l’orbite de LO-19.
La
troisième loi de Kepler permet de calculer le rayon orbital du
satellite.
T2 / R3 = 4 p2 /(GMterre).
R3
= T2 GMterre / (4 p2 )= (6,0 103)2 x 6,67 10-11
x 5,97 1024/(4 x3,142 )= 3,6 1020 ;
R =7,1 106 m = 7,1 103 km.
Altitude du satellite :7,1 103 -6,4 103 ~700 km.
L'hypothèse d'une orbite basse est valide.
Vitesse d'un
avion supersonique.
14. Estimer la vitesse de l’avion par rapport à l’air.
La figure
ci-dessous décrit quant à elle les ondes émises par un avion ayant une
vitesse v > vson. Les surfaces d’ondes s’alignent alors
suivant un cône.
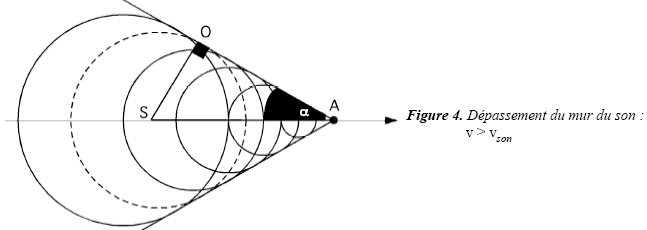
OA : déplacement de
l'onde soit c Dt.
AS : déplacement de l'avion soit v Dt.
cos a = OA / AS =
c / v.
v = c / cos a
avec a = 25° et c
= 340 m/s, célérité du son dans l'air.
Vitesse de l'avion par rapport à l'air : v = 340 / cos 25 ~375 m /s.
375 x3,6 = 1,35 103 km /h.
|
|
|
II. Expérience
de Ives-Stilwell
II.A Raies d'émission atomique.
15. Expression de la force de Coulomb s'exerçant entre deux charges q1 et q2 distantes de d.
F = k q1 q2 / d2 avec k une constante.
Expression de la force donnée dans l'énoncé ( foce attractive entre un proton et un électron ) : F = e2/ (4pe0 ra ).
On en déduit : a = 2.
16. Cas de l'atome d'hydrogène.
Force gravitationnelle entre proton et électron : FG = Gmp me / r2.
Force de Coulomb entre proton et électron : Fe = e2/ (4pe0 r2 ).
Fe / FG = e2/ (4pe0 Gmp me ) =(1,6 10-19)2 /(4 x3,14 x8,85 10-12 x6,67 10-11 x1,67 10-27 x9,1 10-31)~1039.
La force de gravitation est négligeable devant la force de Coulomb.
17. Expression de l'énergie potentielle de l'électron : Ep = - e2/ (4pe0 r ).
L'électron n'est soumis qu'à la force centrale centripète de Coulomb. De plus son mouvement est circulaire.
Le mouvement de l'électron est uniforme à la vitesse de norme v.
accélération a = Fe / me = e2/ (4pe0 r2 me) = v2 / r.
vitesse : v2 = e2/ (4pe0 r me).
Energie cinétique de l'électron : Ec = 0,5 mev2 = e2/ (8pe0 r ).
L'énergie mécanique est la somme de l'énergie potentielle et de l'énergie cinétique :
E = - e2/ (4pe0 r ) + e2/ (8pe0 r )= -e2/ (8pe0 r ).
18. On donne rn vn = nh / (2pme).
Elever au carré : r2n v2n = n2h2 / (2pme)2.
Remplacer v2 par e2/ (4pe0 r me) :
r2n e2/ (4pe0 rn me) = n2h2 / (2pme)2 ; rn e2/ e0 = n2h2 / (pme) ;
rn=n2h2 e0 /( pme e2).
r1=h2 e0 /( pme e2) soit rn = n2 r1.
r1 ~0,1 nm = 10-10 m est le rayon de l'atome d'hydrogène pris dans son état fondamental.
19. Expression de la constante de Plank :
r1=h2 e0 /( pme e2) ; h =[ r1pme e2/ e0]½= e [ r1pme / e0]½.
h = 1,6 10-19 [10-10 x3,14 x9,1 10-31 / (8,85 10-12)]½ ~9,1 10-34 J s.
20. Expression de l'énergie mécanique :
En = -e2/ (8pe0 rn ) = -e2/ (8pe0 r1n2 ).
On pose e = e2/ (8pe0 r1) ; En = -e / n2.
21. Lorsqu'un électron passe du niveau d'énergie Ep au niveau d'énergie En avec p > n, il y a émission d'un photon d'énergie :
Ep-En = -e / p2+ e / n2= e ( 1 / n2-1 /p2).
Longueur d'onde de ce photon : l = h c / [e ( 1 / n2-1 /p2)].
22. Dans le vide 656 nm correspond à une lumière rouge et 486 nm à une lumière bleue.
23. L'électron se désexcite d'un niveau p au niveau n = 2.
On donne 4 longueurs d'onde situées dans le visible :656,3 nm ; 486,1 nm ; 434,0 nm et 410,2 nm.
Dans le visible, il n'y a aucune radiations autres que celles proposées : donc les niveaux excités recherchés se suivent.
A la plus petite longueur d'onde correspond le niveau d'énergie le plus élevé.
A p = 6 correspond 410,2 nm ; à p = 5 correspond 434,0 nm ; à p = 4 correspond 486,1 nm ; à p = 3 correspond 656,3 nm.
24. l = h c / [e ( 1 / n2-1 /p2)]= hc / e [n2p2 / (p2-n2)].
e = e2/ (8pe0 r1)~ (1,6 10-19)2 /(8 x3,14 x8,85 10-12 x10-10) ~1,15 10-18 J.
l(nm)
|
410,2
|
434,0
|
486,1
|
656,3
|
| c / e [n2p2 / (p2-n2)] |
1,17 1027
|
1,24 1027
|
1,39 1027
|
1,87 1027
|
h
|
410,2 10-10 /(1,17 1027)=3,5 10-34
|
3,5 10-34 |
3,5 10-34 |
3,5 10-34 |
.
|
...
|
|
.
|
....
|
Description de l'expérience de Ives-Stilwell.
Dans leur expérience, Ives et Stilwell ont généré un faisceau d’ions
ayant une vitesse de norme v, grâce à un arc électrique et un filament
chaud.

Extrait traduit et adapté de Modern Physics, de K.S. Krane, éd. Wiley.
25. Quel est l'intérêt du miroir ?
Le miroir permet la réflexion des photons émis vers la gauche ( vers le spectrophotomètre ).
26. Dl1 = ± l0 v / c.
Dans cette expression l0 correspond à ll(question 8).
Les grilles accélératrices sont symbolisées par les lignes tiretées à
gauche et à droite de la zone d’accélération. On note U = 30 kV la
différence de potentiel entre ces deux grilles.
27. Les deux plaques sont soumises à une tension de 30 kV. Un champ électrique règne entre les deux plaques.
Ce dernier permet d'accélérer les ions.
28. Les ions possèdent une vitesse négligeable à l'entrée de la zone d'accélération.
L'énergie potentielle électrique est convertie en énergie cinétique dans cette zone d'accélération.
On note m la masse des ions et q = e, leur charge.
e U = ½mv2.
v = (2eU / m)½.
Or DDl = l0 v / c.
DDl = l0 (2eU / m)½ / c.
En posant a = l0 (2e / m)½ / c, on obtient DDl = a U½.
29. Pour enregistrer les raies d'émision des ions au repos, on annule la tension accélératrice U.
Analyse des résultats.
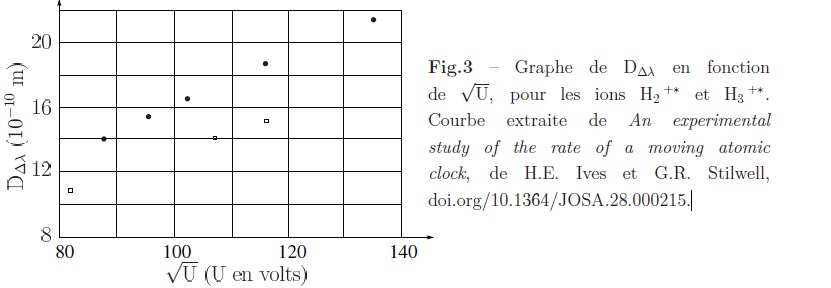
30. Les courbes obtenues semblent-elles en accord avec le modèle théorique ?
La courbe d'équation DDl = a U½ est une droite passant par l'origine et de pente égale à a.
31. Les ions H2+ et H3+ diffèrent par leur masse.
La masse de H2+ est inférieure à celle de H3+ .
La masse intervient au dénominateur dans l'expression de a.
La courbe de pente la plus élevée correspond à H2+ .
32. On note : a2 = l0 (2e / m(H2+))½ / c et a3 = l0 (2e / m(H3+))½ / c.
a2 /a3 =[m(H3+) / m(H2+)]½ =[3mp / (2mp)]½ =1,5½~1,2.
Graphiquement on détermine a2 =0,15 10-10 m V-½ et a3 =0,12 10-10 m V-½ ;
a2 /a3 =0,15 / 0,12 ~1,25, en accord avec la valeur ci-dessus.
33. Soit la grandeur SDl =½ (Dl+ +Dl-)
Dl- = - v / c ll ; Dl+ = v / c ll.
SDl =0 pour un décalage des raies dû uniquement à l'effet Doppler.
Or le graphique indique que SDl croît avec v / c.
Un autre phénomène (effet Doppler relativiste ) intervient donc dans le décalage des raies.
34. La précision du spectrophotomètre est-elle en cause ?
On effectue plusieurs série de mesures et on calcule la moyenne. Cela permet de minimiser l'imprécision de l'appareil.
|
|