Physique,
Concours ESA 2018 ( école de santé des armées).
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
......
.....
|
Exercice 1 ( 5 points)
Traitement d'une tumeur
par échographie.
Le traitement d’une tumeur par échothérapie consiste à y focaliser des
ondes ultrasonores d’énergie élevée de manière à y produire un
réchauffement rapide entraînant la nécrose des tissus tumoraux et ainsi
leur destruction. On utilise ce procédé pour traiter une tumeur de
diamètre 1 cm ; les ultrasons mis en jeu ont une intensité acoustique I
= 108 W.m-2 au niveau du point de focalisation ;
dans les tissus adipeux, la fréquence des ultrasons vaut 3 MHz et leur
vitesse de propagation est de 1500 m.s-1.
Constantes physiques – Aides aux calculs :
Vitesse de propagation du son dans l’air : 340 m.s-1.
Seuil d’audibilité de l’oreille humaine : I0 = 10-12
W.m-2.
Log(2) ~ 0,3 ; Ln(2) ~ 0,7 ; Log(3) ~ 0,5 ; Ln(3) ~ 1,1
1) Les ondes
ultrasonores peuvent-elles se propager dans le vide ? Justifier.
Les ondes ultrasonores sont des ondes mécaniques ; elles ne se
propagent pas dans le vide.
2) Si les ultrasons
utilisés pour l’échothérapie se propagent non plus dans les tissus
adipeux mais dans l’air, la fréquence est-elle inférieure, égale ou
supérieure à 3 MHz ? Justifier.
La fréquence est une caractéristique d'une onde, indépendante du milieu
de propagation. La fréquence reste constante dans l'air et dans les
tissus..
3) Quelle est, en
mètre, la valeur de la longueur d’onde des ultrasons dans les tissus
adipeux ?
l = v
/ f = 1500 / ( 3 106) =5,0 10-4 m= 0,5 mm.
4) Est-il pertinent
de prendre en compte la diffraction des ultrasons par la tumeur ?
Justifier.
Non, le diamètre de la tumeur n'est pas du même ordre de grandeur que
la longueur d'onde des ultrasons.
5) Quelle est, en
décibel, la valeur du niveau d’intensité sonore L des ultrasons
utilisés ?
L = 10 log(I / I0) = 10 log( 108 / 10-12)
=200 dB.
6) Un marteau
piqueur produit un son de 100 dB ; combien de marteaux piqueurs
faudrait-il pour égaler le niveau d’intensité sonore des ultrasons
utilisés lors de cette échothérapie ?
Pour un marteau-piqueur : I = I0 10L / 10 = 10-12
x 1010 = 10-2 W m-2.
Pour n marteaux-piqueurs : 10-2 n = 108 ; n = 1010.
|
...
|
|
Exercice 2. 5 points.
(traitement d’une tumeur
par protonthérapie) (partie 1)
Le traitement d’une tumeur par protonthérapie
consiste à
l’irradier par un faisceau mono énergétique de protons qui perdra la
majeure partie de son énergie dans la tumeur générant ainsi sa
destruction. Les protons utilisés sont au préalable accélérés grâce à
un cyclotron formé d’électrodes semi-circulaires à l’intérieur
desquelles règne un champ magnétique d’intensité B. Sous l’action du
champ magnétique, les protons décrivent une trajectoire circulaire
uniforme de rayon R et de centre C avec une vitesse V.
Dans l’électrode, on suppose que le proton de charge e et de masse m ne
subit que l’action d’une force magnétique F dont l’expression est
donnée.
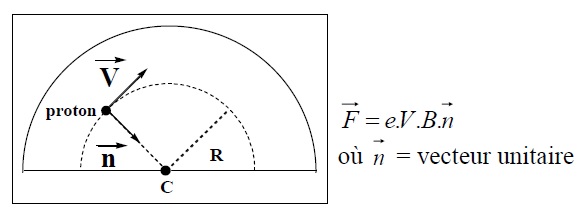
1) En vous aidant
de l’expression de la force magnétique, proposer une unité, dans le
système international, envisageable pour le champ magnétique B.
Force =masse fois accélération ( kg m s-2).
V, vitesse (m s-1) ; e charge électrique ( A s).
B : kg
m s-2 / (A s m
s-1) soit kg A-1 s-2 ou tesla.
2) Dans quel référentiel doit-on se
placer pour étudier le mouvement du proton ?
L'étude est simplifiée en se plaçant dans le référentiel lié au proton.
3) En appliquant la
seconde loi de Newton au proton, établir l’expression de son vecteur
accélération en fonction des grandeurs m, e, V, B et du vecteur
unitaire.
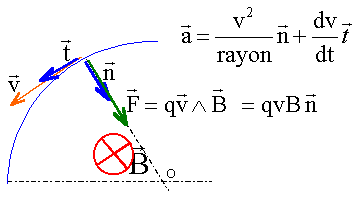
L'accélération est centripète de norme qvB / m = v²
/rayon.
4) Démontrer que le mouvement du
proton dans l’électrode est circulaire uniforme.
Le poids est négligeable devant la force magnétique ; cette force étant
perpendiculaire au vecteur vitesse, ne travaille pas et en conséquence
ne modifie pas l'énergie cinétique du proton. La norme du vecteur
vitesse est constante : le mouvement est uniforme.
5) Etablir
l’expression de la vitesse V du proton en fonction des grandeurs m, e,
R, B.
e V B / m = V2 / R ; e B / m = V / R ; V = e B R / m.
6) Démontrer que
la durée D t nécessaire au
proton pour parcourir la demi-trajectoire circulaire décrite dans
l’électrode admet pour expression : D
t = (p.m) / (e.B).
Le proton décrit la demi-circonférence p R à la vitesse V en Dt seconde.
p R =
V Dt = e B R / m Dt ; D
t = (p.m) / (e.B).
|
....
|
Exercice 3. ( 5 points).
Le traitement d’une tumeur par protonthérapie consiste à l’irradier par
un faisceau mono énergétique de protons qui perdra la majeure partie de
son énergie dans la tumeur générant ainsi sa destruction. On utilise
cette technique pour traiter une tumeur supposée sphérique de centre C
et de rayon R = 1 cm.
Un proton est envoyé en direction de la tumeur ; il arrive à l’entrée E
de la tumeur avec une énergie cinétique ECE = 2.10-11
J et il stoppe son mouvement
au centre C de la tumeur. On suppose qu’entre E et C, le proton est
animé d’un mouvement rectiligne uniformément décéléré durant lequel il
subit une force
de frottement f de norme inconnue. Son poids est négligeable devant f.
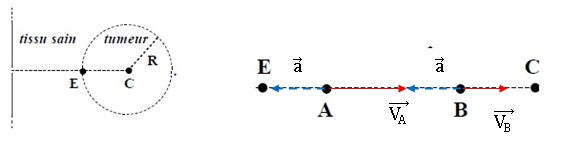
1) On considère
deux points A et B sur la trajectoire EC du proton
a) Représenter par
des flèches en traits pleins les vecteurs vitesses en A et B ;
justifier leurs longueurs relatives.
Le mouvement est décéléré : la vitesse diminue.
b) Représenter par
des flèches en traits pointillés les vecteurs accélérations en A et B ;
justifier leurs longueurs relatives.
Le mouvement est uniformément décéléré : la norme de l'accélération est constante.
2) Etablir
l’expression du travail de la force de frottement entre E et C en
fonction de f et R.
Le travail de f est résistant et vaut : W = -f R.
3) Durant le
mouvement du proton de E vers C, décrire les évolutions de l’énergie
cinétique, de l’énergie potentielle de pesanteur et de l’énergie
mécanique du proton. Justifier vos réponses.
La vitesse diminue, donc l'énergie cinétique décroît.
EC est horizontal : l'énergie potentielle de pesanteur reste constante.
L'énergie mécanique, somme de l'énergie potentielle et de l'énergie cinétique, diminue du travail des frottements.
4) Etablir
l’expression de la norme de la force de frottement f en fonction de ECE
et de R.
En déduire la valeur numérique de la norme de la force de frottement.
Ecrire le théorème de l'énergie cinétique entre E et C ( arrêt ) :
0-½mV2E = - f R ; f = ½mV2E / R = ECE / R =2 10-11 / 10-2 = 2 10-9 N.
Exercice 4 : (5
points) (traitement d’une tumeur par
photothérapie dynamique)
Le traitement d’une tumeur par photothérapie dynamique consiste dans un
premier temps à injecter un médicament photosensible dans la tumeur.
Dans un second temps, ce médicament photosensible est activé en
l’éclairant par une lumière laser qui est guidée jusqu’à la tumeur
grâce à une fibre optique.
Formulaire – Constantes physiques – Aides aux calculs :
Puissance énergétique (W) = Energie (J) / Durée (s)
Nombre d’Avogadro : NA ~ 6,0.1023
particules.mol-1
Célérité de la lumière dans le vide : c = 3,0.108 m.s-1.
Constante de Planck : h ~ 6,0.10-34 J.s
1) On injecte dans
la tumeur 6,0 µg de molécules photosensibles ; sachant que leur masse
molaire moléculaire est de 150 g.mol -1, calculer le nombre
de molécules injectées.
N =m / M NA=6,0 10-6 / 150 x6 1023 = 36 /1,5 1015=2,4 1016.
2) Le laser émet
dans l’air une lumière de longueur d’onde 600 nm à une puissance de 300
mW.
a) Que vaut la
quantité de mouvement d’un photon laser ? Préciser son unité.
p = h / l =6 10-34 / (600 10-9) =1,0 10-27 kg m s-1.
b) Que vaut, en
joule, le quantum énergétique d’un photon laser ?
E = hc / l = 6 10-34 x 3 108 /(600 10-9) =3 10-19 J.
c) Quel est le
nombre de photons émis par le laser en une seconde ?
Puissance ( W) / énergie ( J) = 0,30 / (3 10-19)= 1018.
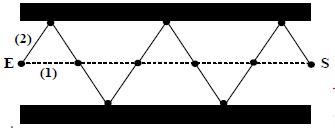
3) Le schéma
ci-dessous est une portion de la fibre optique dans laquelle on a fait
figurer deux rayons lumineux se propageant de E vers S (le rayon (1) en
pointillé se propage en ligne droite ; le rayon (2) en trait plein
subit une suite de réflexions totales au niveau de la gaine de la
fibre).
Pour simplifier l’étude, on suppose que :
- au point E, les deux rayons sont en phase
- la longueur d’onde dans la fibre reste l = 600 nm
- la distance entre deux points consécutifs ( . ) vaut 300 nm
a) Calculer la
différence de parcours des deux rayons (1) et (2) durant leur trajet de
E vers S.
5 x300 = 1500 nm.
b) Déduire de la
question (a) l’état vibratoire (ou état de phase) des deux rayons au
point S.
1500 / 600 =2,5.
La différennce de distance parcourue est égale à un nombre
impaire de demi-longueur d'onde : au point S, les deux rayons sont en
opposition de phase.
c) Déduire de la
question (b) si l’interférence des rayons en S est constructive ou
destructive.
Les interférennces sont destructives en S.
|
|