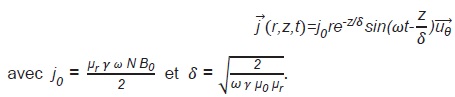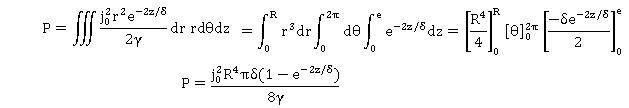La
physique dans la cuisine, choix d'une plaque de cuisson électrique,
Capes physique chimie 2019.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
......
.....
|
Dans
le choix d’une plaque de cuisson interviennent divers critères : la
multiplicité des allures de chauffe, la température à atteindre, mais
également la consommation énergétique.
Les trois types de plaques électriques sur le marché actuellement sont :
- les plaques à foyers en fonte : des résistances électriques chauffent
une plaque en fonte et la chaleur se propage par conduction dans le
récipient à chauffer lorsqu’il est posé sur la plaque en fonte ;
- les plaques vitrocéramique à foyer radiant ou halogène : une source
(résistance électrique ou lampe halogène) transfère l’énergie thermique
au récipient par conduction mais aussi par rayonnement ;
- les plaques à induction (table vitrocéramique à foyer à induction) :
grâce au champ magnétique créé par la bobine plate située dans la
plaque de cuisson, des courants de Foucault apparaissent dans le fond
du récipient à chauffer et produisent de l’énergie
thermique par effet Joule.
Étude énergétique comparée.
Un enseignant de terminale STI2D propose à ses élèves l’activité suivante..
L’un des ménages équipés désire remplacer les foyers en fonte
défectueux et peu adaptés à leurs habitudes culinaires. Il s’interroge
: combien d’années sont nécessaires pour rentabiliser l’achat d’une
plaque à induction à faible consommation en veille par rapport à
celui d’une plaque vitrocéramique sans consommation en veille ?
Données :
- Selon nos mesures, cette famille utilise ses plaques en fonte 400 heures/an.
- Le prix moyen d'une plaque de cuisson à quatre feux : 150 euros pour
une plaque en fonte, 250 euros pour une plaque vitrocéramique, 400
euros pour une table à induction.
- Prix du kWh pour un compteur de 9 kVA résidentiel au tarif bleu au 01/08/2018 : 0,1467 € TTC.
|
Fonte
|
Vitrocéramique
|
Induction
|
Consommation moyenne par heure ( Wh / h)
|
1161
|
999
|
588
|
Puissance de veille (W)
|
0
|
0 à 8
|
8 à 18
|
Durée de la chauffe de 2 kg d'eau de 20°C à 90°C (s)
|
540
|
360
|
267
|
Durée quotidienne d'utilisation ( min / jour)
|
26
|
45
|
58
|
Consommation annuelle d'énergie ( kWh)
|
184
|
281
|
337
|
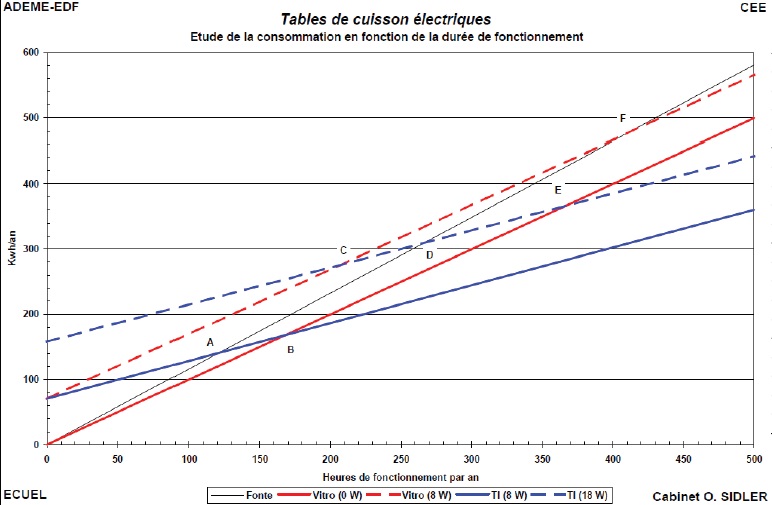
On
peut, grâce aux résultats de l’étude, tracer les caractéristiques de la
consommation en fonction de la durée d’utilisation annuelle des
appareils :
TRAVAIL À EFFECTUER
Q10. Réaliser une correction détaillée des questions 1 à 3 de cette activité.
1. Expliquer les sens de variation opposés des première et dernière lignes du tableau.
Les plaques en fonte possèdent une puissance élevée mais restent peu utilisées. L'énergie annuelle consommée reste donc faible.
Les plaques à induction sont moins puissantes mais sont beaucoup plus utilisées
2. À partir des
données du tableau, établir l’équation qui a permis de tracer la droite
correspondant à une plaque à induction dont la puissance de veille est
maximale. Vérifier la cohérence entre l’équation déterminée et le
graphique.
Energie consommée par an ( kWh / an) = E = Pveille tveille +Putilisation tutilisation.
tveille ~ 1 an = 365 x24 =8760 h.
Plaque à induction : E =0,018 x8760 +0,588 tutilisation ~158 +0,588 tutilisation.
Il s'agit d'une fonction affine.
Coefficient directeur déterminé graphiquement :(440-160) / 500 ~0,56 kWh / h.
E = 0,56 t +160.
3.
À l’aide du graphique, déterminer à partir de quelle durée
d’utilisation annuelle il est préférable d’utiliser une plaque à
induction dont la puissance de veille est maximale par rapport à une
plaque de fonte.
Intersection des droites A et E : t ~260 heures.
Au dela de 260 heures d'utilisation, il faut chosir une plaque à induction.
4. Résolution de problème : répondre à la problématique soulevée par le ménage.
Commenter le résultat obtenu et porter un regard critique sur les hypothèses réalisées lors de la résolution.
Q11. Effectuer la résolution de problème proposée dans la question 4.
Energie consommée par les plaques en fonte : 400 x 1,161 = 464,4 kWh.
Dépense : 464,4 x0,1467~68,1 €.
Energie consommée par les plaques à induction : 400 x 0,588 +0,008 x8760 = 305 kWh.
Dépense : 305 x0,1467~44,8 €.
Gain annuel : 68,1 -44,8 =23,3 €.
Durée : 400 / 23,3 ~17 ans.
Energie consommée par les plaques vitrocéramique : 400 x 0,999 = 399,6 kWh.
Dépense : 399,6 x0,1467~58,6 €.
Gain annuel : 68,1 -58,6 =9,5 €.
Durée : 250 / 9,5 ~26 ans.
Il vaut mieux acheter des plaques à induction, rentabiliser 9 ans plus tôt..
|
...
|
|
.
|
....
|
Réglage de l’énergie thermique produite : exemple d’une plaque de cuisson en fonte
L'unique procédé de transmission de l’énergie thermique utilisé par les
plaques en fonte est la conduction, ce qui limite la rapidité de montée
en température. De plus, leur importante inertie thermique ne favorise
pas la régulation de la température lors d’un changement de
réglages. Ce sont des plaques dites à foyer obscur dans lesquelles une
résistance chauffante en chrome et nickel est encastrée dans
une masse réfractaire, puis recouverte d'une plaque en fonte circulaire.
Les éléments chauffants sont disposés de manière concentrique afin de
favoriser la répartition de l’énergie thermique, le centre n'étant
chauffé que par conduction. L’étude porte sur l’un des foyers en fonte
de la plaque de cuisson électrique à quatre foyers dont les
caractéristiques sont données.
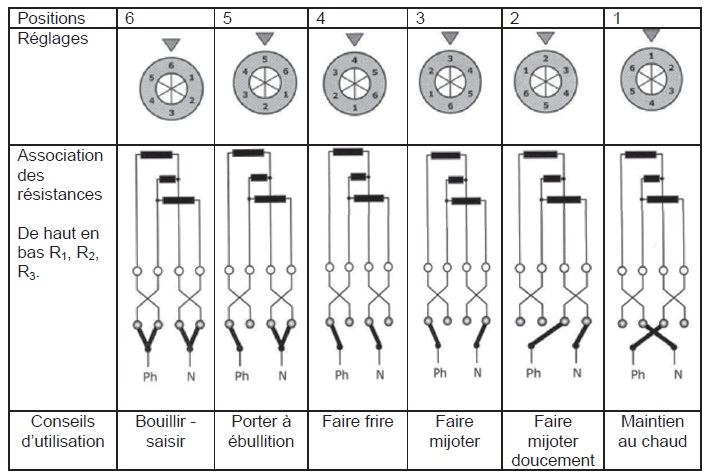
Puissance électrique totale : 2 kW ; tension 230 V.
R1 : 150 ohms / 352 W ; R2 : 80 ohms / 661 W ; R3 : 50 ohms / 1058 W ;
Q12. Pour les
positions de réglage 2, 4 et 6, schématiser l’association des
résistances et calculer la résistance équivalente. En déduire la
puissance « appelée » dans chaque cas puis justifier les conseils
d’utilisation donnés pour chaque réglage en fonction du mode de
cuisson recherché.
Réglage 2 : R3 et R2 en série. Réqui = 50+80=130 ohms.
Puissance appelée : U2 = Réqui =2302/130= 407 W.
Réglage 4 : R3 seule.
Puissance appelée : 1058 W.
Réglage 6 : R1 , R2 et R3 en dérivation.
1 /Réqui = 1/150 +1/80 +1/50 =0,0392 S ; Réqui = 1 / 0,0392 =25,5 ohms.
Puissance appelée : 2302 / 25,5 =2072 W.
Q13. Sur quelle position de réglage faut-il se placer pour vérifier qu’aucune des résistances n’est endommagée ?
Sur la position 1, les trois résistances sont en série.
|
Choix du métal du récipient pour une utilisation avec un chauffage par induction.
Le chauffage par induction repose sur le principe suivant : un
inducteur, bobinage enroulé en spirale et alimenté en courant
sinusoïdal de fréquence f = 25 kHz crée un champ magnétique variable.
Le fond métallique d’une casserole constitue alors l’induit où se
développent des courants de Foucault. L’effet Joule produit par
ces courants chauffe rapidement le fond de la casserole.
On modélise le fond du récipient par une plaque métallique cylindrique
de rayon R = 7,0 cm et d’épaisseur e = 5,0 mm. L’inducteur est
constitué de N = 10 spires.
On assimile le champ magnétique créé par l’inducteur au niveau du fond
du récipient à un champ uniforme et axial, y compris en présence du
récipient. Il s’écrit alors sous la forme : B0(t) cos(wt) avec B0 = 5,0 μT.
Dans la suite du problème on se place en coordonnées cylindriques d’axe (Oz), on appelle r la distance d’un point à l’axe.
Le but de cette partie est de comparer le comportement d'un récipient
en cuivre à celui d'un récipient en acier ferromagnétique. On tiendra
simplement compte du fait que la
conductivité électrique γ et la perméabilité magnétique relative μr des deux métaux considérés n'est pas la même.
Données :
- perméabilité magnétique du vide : μ0 = 4p×10–7 H.m–1 ;
- pour le cuivre : gC = 5,9×107 S.m–1, μr,c = 1,0 ;
- pour l'acier : ga = 0,59×107 S.m–1, μr,a = 100.
Q14. À partir des équations de
Maxwell ainsi que d’arguments de symétries adaptés, justifier
l’existence et la direction du vecteur densité de courant électrique
dans le fond du
récipient.
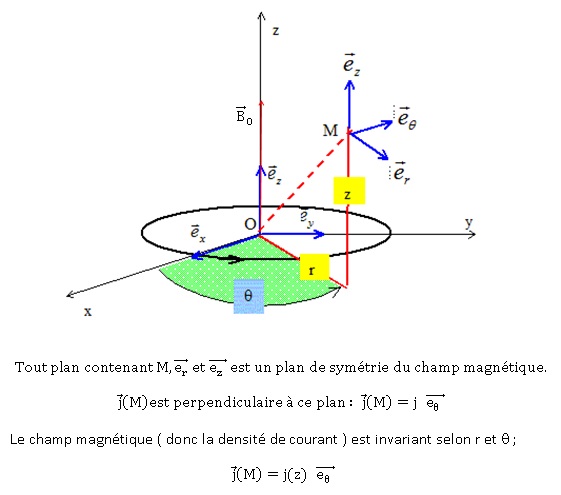
À partir de ces mêmes équations de Maxwell appliquées dans le fond du récipient, on montre, pour l’admettre ensuite, que la densité de courant s’écrit sous la forme :
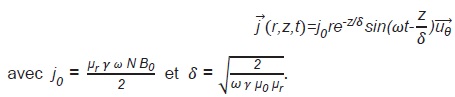
.
Q15. Commenter le sens de variation de l’amplitude ddu vecteur densité de courant avec r et z. Quelle est l’unité de δ et sa signification physique ? Décrire précisément le phénomène physique
modélisé par l’expression en sinus.
La densité de courant :
croît proportionnellement avec le rayon r ;
diminue exponentiellement avec la hauteur z.
d : épaisseur (m) de la couche limite ; au delà de d, la densité de courant est négligeable.
Le terme en sinus décrit la variation sinusoïdale du vecteur densité de courant déphasé de z /d par rapport au champ magnétique.
Q16. On rappelle l’expression de la puissance volumique instantanée dissipée par effet Joule dans un conducteur ohmique donnée par pv = j2 / g. Exprimer la puissance
moyenne totale dissipée dans la plaque.
pv = j2 / g = j02 r2 exp(-2z/d) sin2( wt-z/d) / g.
Valeur moyenne de sin2( wt-z/d) = ½.
Puissance totale moyenne :
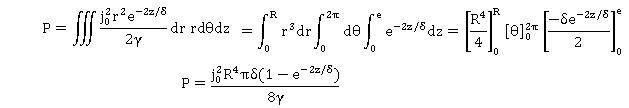
Q17. Calculer puis comparer la puissance dissipée par chaque métal et commenter.
Pour le cuivre :
j0=½µrc gC w N B0 =0,5 x1 x2 /(5,9 107 x6,28x25 103 x10 x5,0 10-6 =2,3 108 A m2.
d2=2 /(w gc µ0µrc =2/(25 103 x5,9 107 x 4 x3,14 10-7 x1)=1,68 10-7 ; d = 4,1 10-4 m.
P =(2,3 108)2 x0,074x3,14x4,1 10-4(1-exp(-2 x5 10-3/(4,1 10-4))) / (8 x5,9 107) ~3,5 W.
Même type de calculs pour l'acier : j0=2,3 109 A m2. d = 1,3 10-4 m. P ~1,1 103 W.
Les récipients en cuivre ne sont pas uitilisés pour les plaques à induction.
|
|
|