Sciences
physique, Concours Avenir 2019.
Son et lumière.
Durée
: 1h 30 min ; réponse exacte : +3 points ; réponse fausse : - 1 points.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
......
.....
|
EXERCICE
1 : Le centre aquatique.
Le centre aquatique est prévu pour accueillir 17 000 visiteurs
lors des épreuves olympiques. Les architectes et ingénieurs doivent
donc faire attention à la sonorisation des lieux. La piscine olympique
est un bassin de longueur D = 50 m, de largeur 10 m et d’une profondeur
H = 2 m.
Données : Capacité calorifique massique de l’eau : Cp = 4 kJ
kg-1 K-1.
Masse volumique de l’eau : reau
= 1000 g L-1.
Conductivité thermique de l’eau : leau = 0,5 SI.
Conductivité thermique de l’air :
lair
= 0,025 SI.
Expression de la
résistance thermique d’une paroi de surface S, d’épaisseur e et de
conductivité thermique l :
Rth = e / (lS).
Intensité sonore de référence ou seuil d’audibilité : I0 = 10-12
W m-2.
Intensité sonore du seuil de danger pour une oreille moyenne : Idanger = 10-3 W m-2.
On considère : log 17
~1,2.
1) L’intensité
sonore d’une onde mesurée par un capteur dépend de la puissance P
captée par unité de :
A) température
B) pression
C) surface. Vrai.
D) volume
2) Le niveau
d’intensité sonore L d’une onde, est relié à l’intensité sonore I de
l’onde par la relation suivante :
A) L = 10 log ( I / I0).
Vrai.
B)
L = 10 log ( I0 / I).
C) L = 10 ln ( I / I0).
D) L = 20 log ( I x I0).
3) Pour une oreille humaine moyenne,
le seuil de danger correspond à un niveau d’intensité sonore de :
A) 60 dB
B) 90 dB. Vrai.
C) 110 dB
D) 120 dB.
L =10 log ( Idanger / I0 ) = 10 log (10-3
/ 10-12) = 90 dB.
4) On considère que
tout visiteur assis dans les gradins du centre aquatique et parlant
normalement, produit une onde sonore au milieu du centre d’un niveau
d’intensité L = 30 dB. On suppose que le centre aquatique est complet
et que chaque visiteur est assis et parle normalement en attendant
l’entrée des sportifs. Le niveau d’intensité sonore, dû aux visiteurs,
au milieu du centre vaut alors :
A) 52 dB
B) 72 dB. Vrai.
C) 102 dB
D) 160 dB.
Pour un seul visiteur : I = I0 x 10L/10 = 10-12
x 103 = 10-9 W m-2.
Pour 17 000 visiteurs : 17 000 x 10-9 = 1,7 10-5 W m-2.
L = 10 log ( 1,7 10-5
/ 10-12) =10 log (17 x 106)~ 12 +60 = 72 dB.
5) Les ondes
sonores sont des ondes :
A) Mécaniques
longitudinales. Vrai.
B) Mécaniques transversales
C) Électromagnétiques longitudinales
D) Électromagnétiques transversales.
6) Pour que deux
ondes sonores qui se croisent interfèrent, il faut qu’elles aient :
A) La même puissance
B) La même fréquence. Vrai.
C) La même intensité
D) Le même niveau sonore.
7) Dans le cas
d’interférences constructives entre deux ondes de longueur d’onde l, la différence de marche d a pour expression :
A) δ=1
B) δ=λ /2
C) δ=n.λ , avec n un
nombre entier. Vrai.
D) δ=(n+12).λ , avec n un nombre entier.
8) Dans le cas de
l’expérience des fentes d’Young, distantes l’une de l’autre de a,
éclairées par une onde de longueur d’onde l, l’expression de
l’interfrange i mesurée par un capteur à une distance D des fentes est :
A) i = a l D.
B) i = l D / a. Vrai.
C) i = a / (2D).
D) i = D /(la).
La piscine est chauffée par une pompe à chaleur de puissance électrique
P. On considèrera que toute l’énergie consommée par la pompe est cédée
à l’eau. Les pertes d’énergie sont donc négligées.
9) Les transferts
thermiques au sein de l’eau de la piscine pour que la température de
celle-ci s’homogénéise se réalise par :
A) Convection. Vrai.
B) Conduction
C) Rayonnement
D) Effet Joule.
10) L’énergie
interne à apporter à l’eau de la piscine pour élever la température de
celle-ci de 1 °C est :
A) 4 kJ
B) 400 kJ
C) 400 MJ
D) 4 GJ. Vrai.
Volume d'eau : 50 x 10 x 2 = 1000 m3.
Masse d'eau : m=1,0 106 kg.
Energie à fournir : m Ceau Dq = 1,0 106 x
4000 x1 = 4 109 J = 4 GJ.
11) La puissance de la pompe à
chaleur nécessaire pour réaliser une élévation de 1°C en 1h de l’eau du
bassin est :
A)P = 1,1 mW.
B) P = 1,1 W.
C) P = 1,1 kW.
D) P = 1,1 MW. Vrai.
Energie (J) / durée
(s) =4 109 / 3600 ~1,1 106 W = 1,1 MW.
12) L’unité de la conductivité
thermique est :
A) W m K.
B) W m-1 K.
C) W m-1 K-1.
Vrai.
D) W m K-1.
13) Pour une couche
d’eau de même dimension qu’une couche d’air, la résistance thermique de
cette couche d’eau est :
A) Plus importante que celle de l’air
B) Égale à celle de l’air
C) Plus faible que celle
de l’air. Vrai.
D) Inversement proportionnelle à celle de l’air.
Rth = e /
(lS) avec lair < leau.
14) L’unité de la résistance
thermique est :
A) Km.
B) Km-1.
C) K W-1.
Vrai.
D) W K-1.
15) Pour une
épaisseur de 1 cm d’eau à la surface du bassin, la résistance thermique
de la couche d’eau est :
A) Rth = 4 10-6 SI.
B) Rth =
4 10-5 SI. Vrai.
C) Rth = 4 10-3 SI.
D) Rth = 4 10-2 SI.
Rth = e /
(lS) =0,01 / (0,5
x 50 x10) =
4 10-5 SI.
|
...
|
|
EXERCICE 2 : L’épreuve du
50 mètres nage libre.
Dans cette partie, on s’intéresse à l’épreuve du 50 mètres nage libre.
Un repère (Oxy) est choisi pour étudier le mouvement du nageur lors de
sa course. L’origine du repère est placée en O. Le nageur, au moment de
son départ pris comme origine des temps, a une vitesse v0 =
10 m /s inclinée d’un angle a=10°
par rapport à l’horizontal. L’étude du mouvement sera décomposée en
deux phases : l’une concernant le saut et l’autre la nage à la surface
de l’eau. Le plongeur sera considéré comme ponctuel. On négligera les
frottements de l’air.
Données : Intensité de pesanteur g = 10 m s-2. Masse du
nageur : m = 80 kg. Masse de la Terre : M = 6 1024 kg. Masse
volumique de l’eau : r =
1000 kg m-3. d : Distance centre de la Terre-Nageur G :
Constante universelle de gravitation.
La poussée d’Archimède exercée sur un corps plongé d’un volume V
dans l’eau est : F =reau
V g avec V : volume d’eau déplacé par la partie du corps plongée dans
l’eau. On considère : cos(10°)≈1

Phase 1 : étude du saut.
Le plongeur part du point A, à t=0 𝑠, avec une vitesse initiale v0
. Il touche l’eau au bout d’une distance horizontale parcourue de x=5
m. On considèrera que le plongeur n’est soumis qu’à l’action de son
poids lors du saut.
16) D’après la
définition du poids du nageur, on peut exprimer l’intensité du champ de
pesanteur terrestre g par la relation :
A) g = GMm / d.
B) g = GM / d.
C) g = GM / d2.
Vrai.
D) g =GMd.
17) L’unité du
champ de gravitation ou champ de pesanteur terrestre g est :
A) N m-1.
B) N s-1.
C) N kg-1.
Vrai.
D) N s-2.
18) L’accélération
du plongeur pendant cette phase a pour expression :

19) Les
coordonnées de la vitesse initiale (Vox , Voy)
du plongeur dans le repère (Oxy) sont :
A) (v0 ; 0)
B) (0 ; v0 )
C) (v0 sin a;
v0
cos a)
D) (v0 cos a; v0 sin a). Vrai.
20) Les coordonnées
de la vitesse v du plongeur en fonction du temps, lors de son saut,
sont :
A) vx(t) =v0
sin a; vy(t) = -gt +v0 cos a.
B) vx(t) =v0 sin a; vy(t) = gt +v0 cos a.
C)
vx(t) =v0 cos a; vy(t) =
-gt +v0 sin a. Vrai.
D) vx(t) =v0 cos a; vy(t) = -gt +v0 cos a.
Le vecteur vitesse est une primitive du vecteur accélération ( 0 ;-g).
Les coordonnées de la vitesse
initiale (Vox , Voy) du plongeur dans le
repère (Oxy) sont :(v0 cos a; v0 sin a).
21) Les coordonnées
de la position du plongeur, lors de son saut, en fonction du temps sont
:
A) x(t) = v0 sin a t ; y(t) = 0,5 gt2
+v0
cos a t +h.
B) x(t) = v0
sin a t ; y(t) =
-0,5 gt2 +v0
cos a t +h.
C)
x(t) = v0 cos a t ; y(t) = -0,5 gt2
+v0 sin a t +h. Vrai.
D) x(t) = v0
cos a t ; y(t) =
0,5 gt2 +v0
sin a t +h.
Le vecteur position est une primitive du vecteur vitesse et la position
initiale a pour coordonnées( 0 ; h).
22) Le plongeur touche l’eau au bout
d’une durée de :
A) Dt = 10 s.
B) Dt = 5 s.
C) Dt
= 1 s.
D)
Dt = 0,5 s. Vrai.
x(t) = v0
cos a t ; 5 = 10
x1 x t ; t = 0,5 s.
23)
La vitesse horizontale au moment de l’impact avec l’eau est :
A) 5 m /s.
B) 10 m / s. Vrai.
C) 25 m /s.
D) 50 m /s.
vx(t) = v0 cos 10 = 10 x 1 = 10 m /s.
|
....
|
Phase 2 : étude de la nage.
On considèrera dans cette phase (questions 24 à 33), que le nageur
étudié a un mouvement rectiligne uniforme de vitesse v = 1,5 m /s sur
les 45 derniers mètres à parcourir dans l’eau.
24) Dans cette
phase, la loi qui est vérifiée en considérant le référentiel terrestre
comme galiléen est :
A) La 1ère
loi de Newton. Vrai ( mouvement rectiligne uniforme)
B) La conservation de la quantité de mouvement
C) La 2nde loi de Kepler
D) La 3ème loi de Newton.
25) Le poids est
ici compensé par :
A) Les frottements de l’air
B) La force de propulsion du nageur
C) La poussée d’Archimède.
Vrai. ( la poussée
est verticale, vers le haut, opposée au poids )
D) Les frottements de l’eau.
26) Le volume du
plongeur dans l’eau ou volume d’eau déplacé par le plongeur est :
A) V = 8 L
B) V = 10 L.
C) V = 80 L. Vrai.
D) V = 100 L.
mg = V reau
g ; V = m / reau=
80 / 1000 = 0,08 m3 = 80 L.
27) La force de
propulsion du nageur est compensée par :
A) Les frottements de l’air
B) La poussée d’Archimède
C) Les frottements de
l’eau. Vrai.
D) Le poids.
28) La durée mise
par le nageur pour parcourir les 45 derniers mètres dans l’eau est :
A) 9 s.
B) 15 s.
C) 18 s.
D) 30 s. Vrai.
t = distance (m) / vitesse ( m/s)= 45 / 1,5 = 30 s.
29) Le nageur,
durant cette phase, est un système :
A) Calorifugé
B) Isolé
C) Pseudo-isolé. Vrai.
D) Ouvert.
30) Au cours du
mouvement, sa quantité de mouvement :
A) Est nulle
B) Diminue
C) Reste constante. Vrai.
D) Augmente.
31) Au cours du
mouvement, la variation d’énergie potentielle du nageur est :
A) nulle. Vrai.
B) -36 kJ
C) 36 kJ
D) 440 kJ.
Le mouvement du nageur s'effectue sur une horizontale, prise comme
origine des altitudes.
32) Au cours du
mouvement, la variation d’énergie cinétique du nageur est :
A) 0 J. Vrai.
B) 60 kJ
C) 90 kJ
D) 120 kJ.
La vitesse reste constante, l'énergie cinétique ne varie pas.
33) L’énergie
cinétique du nageur durant cette phase est :
A) 0 J
B) 40 kJ.
C) 90 J. Vrai.
D) 120 J.
½mv2 = 0,5 x80 x1,52 =90 J.
|
EXERCICE
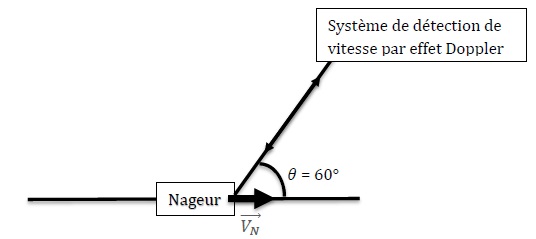
3 : Mesure de la vitesse des nageurs.
Pour mesurer précisément la vitesse des nageurs, un système de mesure
par effet Doppler est installé au plafond du côté de l’arrivée.
Le système envoie des impulsions (paquet) d’ondes électromagnétiques de
fréquence fE = 0,5 GHz vers la surface de l’eau avec un
angle de q = 60°
par rapport à l’horizontale. Les ondes sont réfléchies vers le système
lors du passage du plongeur avec une fréquence fR différente
de celle émise. Le système calcule alors la vitesse du nageur vN
à l’aide de la fréquence fR des ondes qu’il reçoit et la
fréquence fE des ondes qu’il a émises.
Schéma de la situation :
Données : Vitesse v d’une onde électromagnétique dans un milieu
d’indice n et reliée à la célérité c de l’onde dans le vide par : v =c
/ n.
Indice de réfraction de l’eau : neau=1,5. Indice de
réfraction de l’air :nair=1,0
On rappelle : cos 60 = 0,5.
34) La longueur
d’onde dans l’air des ondes électromagnétiques utilisée par le
détecteur est :
A) 𝜆=1,67.10−3 m.
B) 𝜆=6.10−1
m. Vrai.
C) 𝜆=1,67 m
D) 𝜆=6.102 m.
l = c
/ fE = 3,0 108 / (0,5 109) =3 / 5 =
0,6 m.
35) Le domaine
électromagnétique de ces ondes est :
A) Ultraviolet
B) Infrarouge
C) Rayon X
D) Radio. Vrai.
36) Le système
envoie des impulsions d’ondes électromagnétiques de durée 10 ns
chacune. Combien de périodesT contient une impulsion :
A) 1
B) 5.Vrai.
C) 10
D) 20.
T = 1 / fE =1 / (0,5 109) =2 10-9
s = 2 ns.
37) La fréquence de
l’onde reçue fR par le détecteur après réflexion sur le
nageur est telle que :
A) fR
> fE. Vrai. ( Le nageur se rapproche du
système de mesure ).
B) fR < fE.
C) fR = fE.
D) fR est nulle.
38) La différence
de fréquences entre les ondes reçues fR après réflexion sur
le nageur et les ondes émises fE vaut :
A) fR-fE=2
. 𝑉𝑁.cos(60°) /c fE.
Vrai
B) fR-fE= -2 . 𝑉𝑁.cos(60°)
/c fE. ( fR>fE)
C) fR-fE=0.
D) fR-fE=VN.
( relation non homogène vis à vis des unités )
39)
La variation de fréquence détectée entre les signaux émis et reçu est 5
Hz lors du passage du nageur. La vitesse du nageur est alors :
A) 10 m /s.
B) 9 m /s.
C) 6 m /s.
D) 3 m /s. Vrai.
fR-fE=2 . 𝑉𝑁.cos(60°)
/c fE.
5 =2 . 𝑉𝑁 x0,5 /(3 108)
x 0,5 109 ; 5 = VN x 5 / 3 ; VN
= 3 m /s.
40)
Si les ondes émises par le détecteur étaient envoyées à la verticale de
la surface de l’eau (q
= 𝟗𝟎°), alors la mesure de la vitesse du nageur serait :
A) Plus précise
B) Moins précise
C) Impossible à réaliser.
Vrai ( cos 90 = 0 ; fR-fE = 0)
D) Il manque une information pour répondre.
Lorsque les ondes arrivent à la surface air-eau, une partie est
réfléchie et une autre réfractée.
41) La vitesse des
ondes réfractées dans l’eau est :
A) v=4,5.108 m /s.
B) v=3.108 m /s.
C) v=2.108 m
/s. Vrai.
D) v=1,5.108 m /s.
v = c / neau = 3 108 / 1,5 =2.108 m /s.
42)
La longueur d’onde des ondes dans l’eau :
A) Est identique à celle dans l’air
B) Est inférieure à celle
dans l’air. Vrai.
C) Est supérieure à celle dans l’air
D) Appartient au domaine du visible.
leau
=veau / f =c /(nf) =lair / n = lair
/ 1,5.
43) La
fréquence des ondes :
A) Reste identique quand
les ondes changent de milieu de propagation. Vrai.
B) Diminue quand les ondes changent de milieu de propagation
C) Augmente quand les ondes changent de milieu de propagation
D) Dépend de la température du milieu.
EXERCICE 4 : Expérience
sur le son et la lumière.
La compétition sera enregistrée et retransmise dans le monde entier.
Pour cela, des caméras utilisant la technologie HD seront présentes
dans le centre aquatique et reliées à la régie par fibre optique.
Chaque caméra sera dotée d’un capteur comportant 400 lignes et 800
colonnes de pixels et permettra l’acquisition de 50 images par seconde.
Le codage des couleurs fera intervenir 3 pixels, chacun codé sur un
octet : un rouge, un vert et un bleu. L’image sera donc codée en RVB.
Dans ce codage, les couleurs sont obtenues par synthèse additive.
Données :
On considère : log(2) ≈ 0,3
Atténuation en décibel d’un signal se propageant dans une fibre optique
de puissance à l’entrée de la fibre Pentrée et de puissance
en sortie Psortie : AdB=10.log(Pentrée
/ Psortie)
Coefficient d’atténuation linéique d’un signal se propageant dans une
fibre optique de longueur L : a
= AdB / L.
44) Un pixel sera
codé sur :
A) 3 bits
B) 8 bits
C) 16 bits
D) 24 bits. Vrai.
3 octets soit 3 x8 = 24 bits.
45) Un pixel sera
codé à l’aide de :
A) 64 valeurs décimales allant de 1 à 64
B) 255 valeurs décimales allant de 1 à 255
C) 256 valeurs décimales
allant de 0 à 255. Vrai.
D) 512 valeurs décimales allant de 0 à 511.
46) La taille de
l’image en octets sera de :
A) 7,68 Mo
B) 2,56 Mo
C) 960 ko. Vrai.
D) 320 ko
400 x 800 x 3 = 960 000 octets = 960 ko.
47) Le débit
nécessaire pour transmettre les images captées sera de :
A) 384 Mbits / s. Vrai.
B) 128 Mbits / s.
C) 16 Mbits / s.
D) 7,68 Mbits / s.
960 x8 =7680 bits par image soit 7860 x 50
= 384 000 kbits ou 384 Mbits par seconde.
48) Le triplet de
valeurs décimales codant un pixel blanc est :
A) (0,0,0)
B) (255,0,0)
C) (0,255,0)
D) (255,255,255). Vrai.
49) Le nombre de
trinômes de valeurs décimales (R,V,B) possibles pour coder les couleurs
avec le codage RVB est :
A) 3
B) 8
C) 256
D) 16777216. Vrai.
224 = 16 777 216.
50) Une mémoire
tampon de 4,8 Go est disponible pour les ralentis. Quelle est la durée
maximale de l’enregistrement d’un ralenti ?
A) Δ𝑡=10 s
B) Δ𝑡=100 s. Vrai.
C) Δ𝑡=10 min
D) Δ𝑡=100 min.
4,8 109 / (9,6 105 x50) =100 s.
Le signal reçu par les caméras est numérisé et ensuite envoyé à une
fréquence de 800 MHz à la régie centrale placée à environ 500 m de
chaque caméra.
51) L’unité du
coefficient d’atténuation linéique du signal lors de sa propagation
dans la fibre optique est :
A) W m-1.
B) W m
C) dB m-1.
Vrai.
D) dB m.
52) Si la puissance
du signal est divisée par deux à sa réception en régie, alors le
coefficient d’atténuation linéique vaut :
A) 6 10-4 SI.
B) 6 10-3 SI. Vrai.
C) 2 10-2 SI.
D) 3 SI.
AdB=10.log(Pentrée /
Psortie) = 10 log 2 = 10 x0,3 = 3 dB ; a = AdB /
L = 3 / 500 = 6 10-3 dB / m.
Les caméras sont équipées de matériaux qui
absorbent certaines ondes électromagnétiques et grâce à un système,
l’énergie captée est transformée en énergie électrique.
Nous étudierons dans les questions suivantes différents types
d’interactions entre des photons et la matière.
53) Pour un atome,
le photon de fréquence n,
qu’il doit absorber pour passer d’un niveau d’énergie E0 à E1,
a pour expression :
A) n = h(E0-E1).
B) n
= (E1-E0) / h. Vrai.
C) n
= h/ ((E0-E1)hc).
D) n
= h(E0-E1) / c.
54)
La longueur d’onde du photon émis par un atome lorsqu’il se désexcite
et perd une énergie DE
= 3,2 eV est de :
A) 5,6.10−6 m
B) 350 nm. Vrai.
C) 6,25.10−3 m
D) 1,12 µm.
l = hc / DE = 6 10-34 x 3 108
/ (3,2 x1,6 10-19) =3,5 10-7 m = 350 nm.
55) Le
fonctionnement d’un laser met en jeu :
A) Le phénomène d’émission spontanée de photon
B) Le phénomène d’absorption de photon
C) Le phénomène d’émission stimulée de photon
D) Les trois phénomènes
cités en A, B et C. Vrai.
Dans le cas de l’effet Compton, un photon de quantité de mouvement p et
de fréquence n
vient collisionner un électron au repos et très faiblement lié à un
atome. Le photon change alors de direction et perd de l’énergie. Il
part après la collision avec une quantité de mouvement p' et une
fréquence n’.
L’électron est éjecté de l’atome avec une énergie cinétique Ec tel que
Ec = ℎ(n-n ′).
56) La quantité de
mouvement d’un photon de fréquence n et de longueur d’onde l dans le vide s’exprime
par la relation suivante :
A) p = mc
B) p = h n.
C) p = h / l. Vrai.
D) p = n /h.
57) Lors de l’effet
Compton entre un photon de fréquence n = 4 GHz et un électron, le
photon repart avec une fréquence n’ = 1 GHz. L’électron
acquiert alors une vitesse égale à :
A) 10 m /s.
B) 200 m /s.
C) 2000 m /s. Vrai.
D) 10 000 m /s.
½mv2 = h(n-n') = 6 10-34 x3
109 =1,8 10-24 J.
v2 = 2 x1,8 10-24 / (9 10-31) =4 106
; v = 2 103 m/s.
58) Si l’électron éjecté est relativiste, alors la durée Dtm pour aller
d’un point A à un point B dans le référentiel terrestre (considéré
comme galiléen), est reliée à la durée propre Dtp entre ces deux événements par la relation
:

Lorsque des rayons X sont émis sur certains matériaux, un phénomène de
diffraction apparaît. Ce phénomène va permettre d’avoir accès à des
informations sur la structure du matériau.
59) Ce phénomène
met en évidence :
A) La dualité onde-particule
B) L’aspect ondulatoire de
la lumière. Vrai.
C) L’aspect corpusculaire de la lumière
D) L’aspect ondulatoire de la matière.
60) Lors du
phénomène de diffraction à l’infini d’une onde électromagnétique par
une fente, la largeur de la tache centrale de diffraction qui se forme
sur un capteur augmente lorsque :
A) La longueur d’onde de
l’onde diffractée augmente. Vrai.
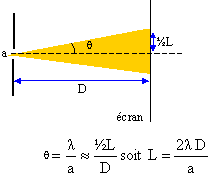
B) La taille de la fente augmente
C) La longueur d’onde de l’onde diffractée diminue
D) La distance fente capteur diminue
|
|
|




