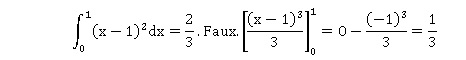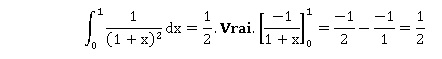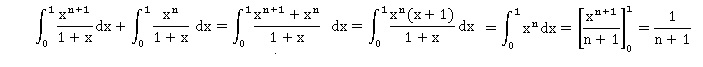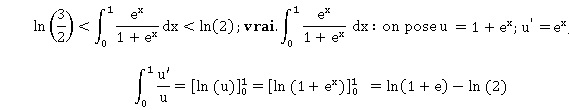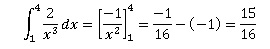Mathématiques,
Concours Advance 2019.
Durée
: 1 heure 30 ; exercices 1 à 6 obligatoires ; exercices 7 à 14 : 6
questions au choix.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
......
.....
|
1-
A. La limite en plus l'infini de A = (x2 -x) / (2x2+1) est égale à 1 /2. Vrai.
A=(1-1 /x) / 2+1/x2).
1 /x et 1/x2 tendent vers zéro si x tend vers plus l'infini.
B. La limite en plus l'infini de x /ex est égale à zéro. Vrai.
Par croissance comparée, ex croît plus vite que x.
C. La limite en zéro de ln(x) est égale à zéro. Faux. ( moins l'infini )
D. Si 2 ln(a)+1 >0 alors a > e½. Faux.
2ln(a)+1 = ln(a2) +1>0 ; ln(a2) > -1 ; a2 > e-1 ; a > e-½.
E. Sur ]0 ; +oo[ la dérivée de la fonction f(x) = x ln(x) est f '(x) = ln(x). Faux.
On pose u =x et v = ln(x) ; u' = 1 ; v' = 1/x ; u'v +v'u = ln(x) +1.
2.
Le plan complexe est muni d’un repère orthonormal d’origine O. Pour tout point M du plan, l’affixe de M est noté ZM.
A, B et C désignent trois points du plan distincts de O.
A. Si Z = (1+i) / (2½-i 6½) alors |Z| =0,5 et arg(Z) =7p/12 (2p). Vrai.
Z = (1+i) (2½+i 6½) / 8 =[(2½-6½) +i(2½+6½)] / 8 ;
|Z| =[(2½-6½)2 +(2½+6½)2 ]½ / 8 =4 / 8 = 0,5.
Z = [(2½-6½) +i(2½+6½)] / 4 =0,5 ( cos(7p/12) + i sin(7p/12).
B. Si Z = -2 [cos(3p/4) + i sin(3p/4)], alors |Z| =2 et arg(Z) = -3p/4(2p). Faux.
Z =( 2½ -i 2½). |Z| = (2+2)½ =2.
Z = 2 [ -cos(3p/4) - i sin(3p/4)] = 2[ -cos(3p/4) - i sin(3p/4)] = 2[ cos(-p/4) + i sin(-p/4)]
C. Si les points A et B sont symétriques par rapport à O alors ZA = conjugué de ZB. Faux.
Le ressort étiré revient à sa position d'équilibre ( déplacement vers
la gauche) du mobile ( système étudié )
D. Si |ZA| =|ZB|=|ZC|, alors ABC est un triangle équilatéral. Faux.
A, B et C sont situés sur le même cercle de centre O.
E. Si arg(ZA) = p + arg(ZB) alors O, A et B sont alignés. Vrai.
3.
f est une fonction définie et dérivable sur un ensemble D.
A. Si D = R et f(x) =(x2-1) / (x2+1) alors f '(x) = 4x / (x2+1)2. Vrai.
On pose u = x2-1 et v = x2+1 ; u' = 2x ; v' = 2x ;
(u'v-v'u) / v2 = 2x ( x2+1 -x2+1)/ (x2+1)2 = 4x / (x2+1)2.
B. Si D = R* et f(x) = (x2-x) e1/x alors f '(x) = e1/x(2x2-2x+1) / x. Vrai.
On pose u = x2-x et v = e1/x; u' = 2x-1 ; v' = -e1/x / x2.
u'v +v'u = (2x-1) e1/x -(x2-x)e1/x / x2 =e1/x (2x-1-1+1/x) =e1/x(2x2-2x+1) / x.
C. Si D=R* et f(x) = ln(x2+1) alors f '(x) = 1/(1+x2). Faux.
On pose u = 1+x2 ; u' = 2x ; f '(x) = u' /u = 2x / (1+x2).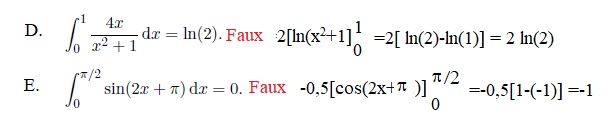 4. Soit f la fonction définie sur R par f(x) = xe1−x et C la courbe représentant f dans un repère orthonormé.
4. Soit f la fonction définie sur R par f(x) = xe1−x et C la courbe représentant f dans un repère orthonormé.
Soit d la droite d’équation y = e x + 15 et D la droite d’équation y = x.
A. La limite en plus l'infini de f(x) est égale à plus l'infini. Faux.
e1-x tend vers zéro quand x tend vers plus l'infini.
B. La limite en moins l'infini de f(x) est égale à moins l'infini. Vrai.
C. Pour tout réel x, f '(x) = (1-x) e1-x. Vrai.
On pose u = x et v =e1-x ; u'=1 et v' = -e1-x ;
u'v +v'u = e1-x -xe1-x .
D. Il existe une tangente T à C qui est parallèle à la droite d. Vrai.
Coefficient directeur de T : (1-x) e1-x ; pour x = 0 ce coefficient vaut e.
E. C est en dessous de la droite D sur ]−∞, 0[. Vrai.
sur ]−∞, 0[, xe1−x est inférieur à e x +15 .
|
...
|
|
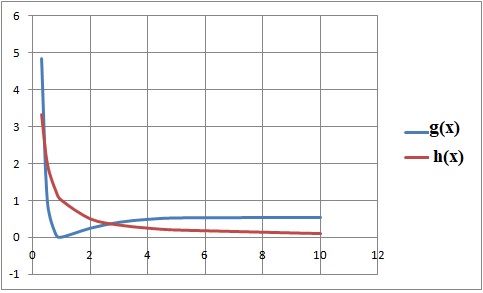
5. Soit g la fonction définie sur ]0,+∞[ par g(x) =(ln(x))2 / x, représentée par la courbe C dans un repère orthonormal.
Soit h la fonction définie sur ]0,+∞[ par h(x) =1 /x, représentée par la courbe C′.
A. La limite en zéro de g(x) est égale à zéro. Faux.
(ln(x))2 tend vers plus l'infini quand x tend vers zéro.
B. Pour tout réel x strictement positif, g′(x) =[2 ln(x) -(ln(x))2] / x2. Vrai.
On pose u =( ln(x))2 et v = x ; u' = 2 ln(x) / x ; v' = 1.
(u'v-v'u) / v2 = (2ln(x) -( ln(x))2 ) / x2 .
C. Pour tout réel x strictement positif, g(x) /2 =[ln(x½) / x½]2. Faux.
[ln(x½) / x½]2 =[ ln(x½)]2 / x = [0,5 ln(x)]2 /x.
D. C admet une asymptote parallèle à l’axe des abscisses. Vrai.
E. C est au-dessus de C′ sur ]1 /e ; +oo[ . Faux.
(ln(x))2 / x -1/x =[(ln(x))2 -1] / x > 0 si x appartient à ]1 /e ; +oo[
6.
Un magasin d’électroménager vend deux modèles de robot au même prix et de marques M1 et M2.
Les deux robots ont les mêmes caractéristiques et sont proposés en deux couleurs : noir et blanc.
D’après une étude sur les ventes de ces deux modèles, 70 % des acheteurs ont choisi le robot M1 et, parmi eux, 60 % ont préféré la couleur noire. Par ailleurs 20 % des clients ayant acheté un robot M2 l’ont choisi de couleur blanche.
On utilise la liste des clients ayant acheté l’un ou l’autre des robots précédemment cités et on choisit un client au hasard.
Soient A et B deux événements indépendants d’un même univers tels que P(A) = 0,3 et P(A ∪ B) = 0,65.
a. La probabilité qu’un client choisi au hasard ait acheté un robot M2 de couleur noire est égale à 6 /25. Vrai.
b. La probabilité qu’un client choisi au hasard ait acheté un robot de couleur noire est égale à 6 /25. Faux.
c. Le client a choisi un robot de couleur noire. La probabilité qu’il soit de marque M2 est égale à 33 / 50. Faux.
d. La probabilité de l’événement B est égale à 0,5.Vrai.
e. A et B sont indépendants. Vrai.
|
....
|
7.
Soit f la fonction définie par f(x) = ln((1-ex)2) et C la courbe représentant f dans un repère orthonormal du plan.
a. Pour tout x non nul, f(x) > 0. Faux.
Par exemple f(0,01) = -9,2.
b. L’axe des abscisses est une asymptote de C en moins l'infini. Vrai.
En moins l'infini, ex tend vers zéro ; 1-ex tend vers 1 et ln((1-ex)2) tend vers zéro.
c. Pour tout x non nul, f(x) = 2 ln(1 − ex). Faux.
ln(1 − ex) n'est défini que pour 1-ex positif.
d. Pour tout x non nul, f(x) >0 si et seulement si x < 0. Faux.
e. f est décroissante sur ]−∞, 0[. Vrai.
On calcule f '(x) en posant v =(1-ex) ; u =v2 ; u ' = 2v v ' = - 2ex (1-ex).
f '(x) = u' / u = - 2ex / (1-ex) ; sur ]−∞, 0[, 2ex / (1-ex) est positif et f '(x) est négative.
8. Suite.
Soit (un) la suite définie par u0 = 1 et pour tout entier n, un+1 =un / 3 +n-2.
Soit (vn) la suite définie pour tout entier n par vn = −2un + 3n −10,5.
On considère l’algorithme ci-dessous.
N est un entier, U est un réel
U = 1 ; N = 0 ;
Tant que (U < 0 ou N = 0)
U = U /3 +N-2
N = N+1
Fin Tant que
Afficher U
a. u3 = − 14 / 27. Vrai.
u1 =u0 / 3 +0-2 = 1 /3 -2 = -5 /3 ;
u2 =u1 / 3 +1-2 = -5 / 9 -1 = -14 / 9 ;
u3 =u2 / 3 +2-2 = -5 / 9 -1 = -14 / 27.
b. L’algorithme affiche la valeur de u3. Faux.
N
|
U
|
(U < 0 ou N = 0) |
0
|
1
|
Vrai
|
1
|
u1 =-5 /3
|
Vrai
|
2
|
u2 = -14 /9 |
Vrai
|
3
|
u3 = -14 /27 |
Vrai
|
4
|
u4 = -14 /81+3-2= 67 / 81
|
Faux
|
c. Pour tout entier n, ( n > 5 entraîne un > n-3). Vrai.
un+1 -(n+1-3) =un+1 -n+2 =un / 3 +n-2 -n +2 = un / 3.
Pour n > 4, un / 3 est positif.
d. (vn) est une suite géométrique de raison 3. Faux.
vn+1 = −2un+1 + 3(n+1) −10,5.
vn+1 = −2(un / 3 +n-2) + 3(n+1) −10,5 = -2un / 3-2n +4 +3n +3 -10,5 = -2un / 3 +n-3,5 = 3(-2un +n /3- 10,5) différent de 3 vn.
e. un tend vers plus l'infini quand n tend vers plus l'infini. Vrai.
un+1 =un / 3 +n-2.
un / 3 est positif et n-2 tend vers plus l'infini.
|
9. Suite.
Soit (un) la suite définie par u0 = 4 et, pour tout n entier, un+1 = f(un) où f est une fonction définie et dérivable sur R.
Soit (vn) la suite définie par v0 = 1 et, pour tout n entier, ln(vn+1) = ln(vn) − 1.
a. Si pour tout réel x, f ′(x) < 0 alors (un) est strictement décroissante. Faux.
Par exemple si f(x) = -x : f '(x) = -1, négative.
u1 = f(u0) = f(4) = -4 ; u2 = f(u1) = f(-4) =16.
b. (vn) est une suite géométrique. Vrai.
ln(vn+1) - ln(vn) =− 1 ; ln ( vn+1 / vn) = -1 ; vn+1 / vn =e-1 ; vn+1 =e-1 vn .
c. (vn) est convergente. Vrai.
vn+1-vn = (e-1 -1) vn négatif , la suite est décroissante et minorée, donc elle converge.
d. La suite (tn) définie pour tout n entier par tn =(n2-200)n½ est décroissante. Faux.
t0=0 ; t1 = -199 ; t2 = -196 x2½ ~ -277 ; t3 = -191 x3½ ~ -330 ; t4 = -184 x2 = -368 ; t5 = -175 x 5½ ~ -391 ; t6 = -164 x6½~ -402 ;
t10 = -100 x10½~ -316 ; t15 = 25 x15½~ 96.
e.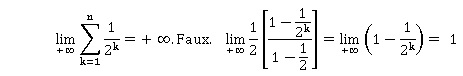
10. f est une fonction définie sur R.
a. Si pour tout réel x > 1, 1 +1 / x < f(x) < (x2+x+10)/ (x2+1) alors la limite en l'infini de f(x) est égal à 1. Vrai.
En plus l'infini : 1 +1/x tend vers 1 ;
(x2+x+10)/ (x2+1) = (1 +1 /x +10 /x2) / (1 +1/x2) tend vers 1 si x tend vers plus l'infini.
b. Si f(x) = 2x + 3 − sin(2x) alors pour tout réel x, f(x) < 2x + 2. Faux.
Si x = 0 ; f(0) =3 > 2.
c. La limite en plus l'infini de 2x sin(1/(2x)) est égale à 1. Vrai.
1 /(2x) tend vers zéro si x tend vers plus l'infini ; par suite au voisinage de zéro, sin(1/(2x))est équivalent à 1 /(2x).
2x * (1/2x) = 1.
d. En plus l'infini, la limite de (3 +2n) / (3 +4n) est égale à 1. Faux.
2n [3 / 2n+1 ] / [4n( 3 /4n +1] =[2 /4]n [(3 / 2n+1 ) / ( 3 /4n +1)] = 0,5n [(3 / 2n+1 ) / ( 3 /4n +1)]
En plus l'infini : 3 / 2net 3 /4n tendent vers zéro.
De plus 0,5n tend vers zéro.
e. Si 0 < x < 1 alors la limite en plus l'infini de [(1-x)n(1+x)n] est égale à plus l'infini. Faux.
[(1-x)(1+x)]n =(1-x2)n ; (1-x2) < 1 ;
(1-x2)n tend vers zéro si n tend vers plus l'infini.
11. Nombres complexes.
Dans
le plan complexe muni d’un repère orthonormal d’origine O, on considère
les points E et F d’affixes respectives −2 + i et 2 + 4i et E
l’ensemble des points M d’affixe z vérifiant
|z + 2 − i| = |z − 2 − 4i|.
Pour tout point M du plan, l’affixe de M est notée zM.
a. Le point G d’affixe 3 −1,5 i appartient à E . Vrai.
|z + 2 − i| = |3-1,5i + 2 − i| =|5-2,5i| =(52+(-2,5)2)½ =31,25½.
|z − 2 − 4i| =|3-1,5i -2-4i|=|1-5,5i| = (12 +(-5,5)2)½ =31,25½.
b. E est le cercle de diamètre [EF]. Faux.
Si le point E appartient à l'ensemble E :
|-2+i+2-i| = 0 ; |z − 2 − 4i| = |-2+i -2-4i| =|-4-3i| différent de zéro.
c. Le triangle OEF est rectangle. Vrai.
OE2 = (-2)2 +12 =5 ; OF2 = (2)2 +42 =20 ;
EF2 =42 +32 =25 = OE2 + OF2 .
D'après la réciproque du théorème de Pythagore, le triangle OEF est rectangle en O.
d. Si zA = 2 − 3i, zB = −26 + 18i et zC = −2 alors A, B et C sont alignés. Vrai.
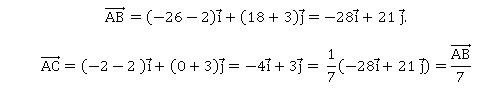
e. Si zA = 3 exp(2ip/3) et zB = 2 exp(-5ip/6) alors le triangle OAB est rectangle. Vrai.
arg(zA) = 2p/3 ; arg(zB) = -5p /6 = -5p /6 +2p = 7 p / 6.
arg(zB) -arg(zA) =7 p / 6 -2p/3 =7 p / 6 -4p/6 =3p/6 = p /2.
12. Géométrie dans l'espace.
L’espace est rapporté à un repère orthonormal.
On considère les points suivants définis par leurs coordonnées : A(1;−1; 2), B(3; 3; 8), C(−3; 5; 4) et D(1; 2; 3).
On note d la droite ayant pour représentation paramétrique
x = 1 + t ; y = −1 + 2t , z = −2 + 3t avec t réel.
On note d′ la droite ayant pour représentation paramétrique
x = 1 + k ; y = 3 + k ; z = 4 − k avec k réel.
On note P le plan d’équation x + y − z + 2 = 0.
a. Le point C appartient à la droite d. Faux.
Hypothèse : C appartient à cette droite d :
xC = 1 + t = -3 soit t = -4 ; y = −1 + 2(-4) = -9 différent de yC. L'hypothèse est fausse.
b. Les droites d et d′ sont parallèles. Faux.
Coordonnées du vecteur directeur de la droite d : (1 ; 2 ; 3).
Coordonnées du vecteur directeur de la droite d' : (1 ; 1 ; -1).
Ces deux vecteurs ne sont pas colinéaires.
c. Le plan P contient la droite d et est orthogonal à la droite d′. Faux.
Hypothèse : le plan contient la droite d.
x + y − z + 2 = 0 soit 1+t +(-1+2t) -(-2+3t) +2 =0 ; 4 +0t = 0, impossible. L'hypothèse est fausse.
d. Le triangle BCD est rectangle. Vrai.
BC2 =(-3-3)2 +(5-3)2 +(4-8)2 =36+4+16=56.
BD2 =(1-3)2 +(2-3)2 +(3-8)2 =4+1+25=30.
DC2 =(-3-1)2 +(2-5)2 +(3-4)2 =16+9+1=26.
BC2 =BD2 +DC2 ; d'après la réciproque du théorème de Pythagore, le triangle BCd est rectangle en D.
e. On note P′ le plan contenant la droite d′ et le point A. Un vecteur normal à ce plan est 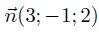 . Vrai. . Vrai.
Hypothèse : 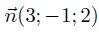 est un vecteur normal au plan P'. est un vecteur normal au plan P'.
Equation de P' : 3x -y +2z +d = 0.
A appartient à ce plan P' : 3 -(-1) +2*2 +d = 0 ; d = -8.
d' appartient à ce plan : 3(1+k) -(3+k) +2(4-k) -8 = 0 ; 8- 8+0k = 0 est vérifié.
13.
On considère les deux fonctions f et g définies par f(x) = (x−1)2 et g(x) = −x+1 représentées graphiquement par leurs courbes respectives Cf et Cg.
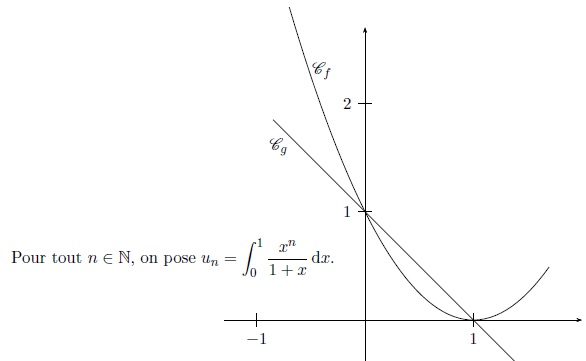
a. L’aire du domaine compris entre Cf et Cg pour x ∈ [0, 1] est égale à 1/ 6. Vrai.
Aire comprise entre la courbe Cf, l'axe des abscisses et les droites d'équation x =0 et x = 1.
[(x-1)3 / 3]01=[0 -(-1)3] / 3 = 1 /3.
Aire comprise entre la courbe Cg, l'axe des abscisses et les droites d'équation x =0 et x = 1.
1 x 1 /2 = 0,5 ;
aire du domaine compris entre Cf et Cg pour x ∈ [0, 1] : 0,5 -1 /3 = 1 /6.
b.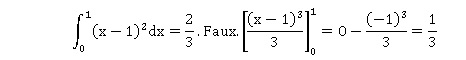
c.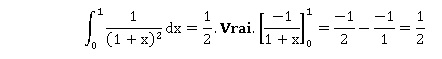
d. Pour tout n ∈ N, un+1 + un =1 /(n+1). Vrai.
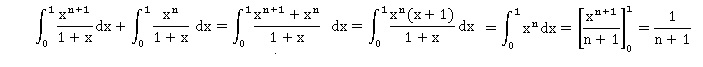
e.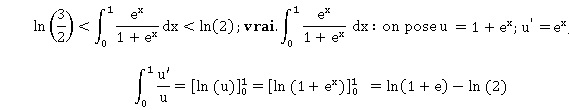
14.
Le temps d’attente, exprimé en minutes, à un
guichet, est une variable aléatoire T qui suit une loi exponentielle de
paramètre 0,7.
Marc se rend à son travail à pied ou en bus. Dans la ville où il habite, il pleut un jour sur quatre.
Lorsqu’il pleut, Marc se rend en bus à son travail dans 80 % des cas.
Lorsqu’il ne pleut pas, il se rend à pied à son travail dans 60 % des cas.
a. La probabilité qu’un client attende moins de 5 minutes à ce guichet est égale à
(e3,5 − 1) /e3,5 . Vrai.
l = 0,7 ; P(T < 5) = 1-e-5x0,7=1-e-3,5.
b. Sachant qu’un
client attend depuis 5 minutes, la probabilité qu’il attende au total
plus de 10 minutes à ce guichet est égale à e−3,5. Vrai.
La loi exponentielle est sans mémoire ; PT =5(T >10) = P(T > 5) =e−3,5.
c. Marc prend le bus un jour sur deux. Vrai.
Soit A l'événement " il pleut" et B l'événement " Marc prend le bus".
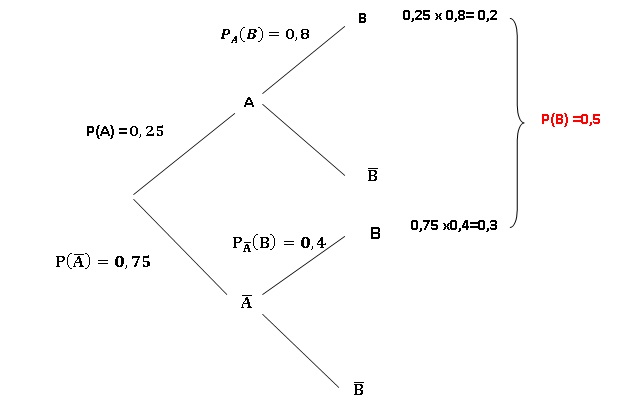
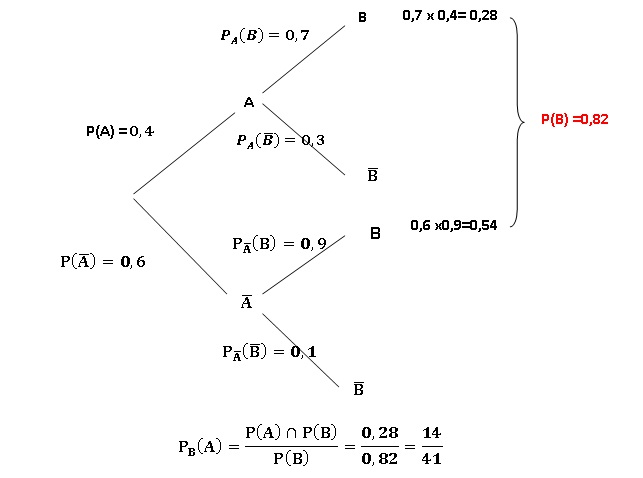
d. Soient A et B deux événements liés à une même épreuve aléatoire qui vérifient : P(A) = 0,4, PA(B) = 0,7
et P non A(non B)=0,1.
Alors la probabilité de l’événement A sachant que l’événement B (PB(A) )est réalisé est égale à14 / 89. Faux.
e. Soit X une
variable aléatoire prenant ses valeurs dans l’intervalle [1,+∞[ et dont
la loi de probabilité admet comme densité la fonction f définie par
f(x) =
2 / x3. Alors P(1 < X < 4) = 15 / 16. Vrai.
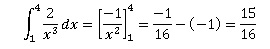
|
|
|

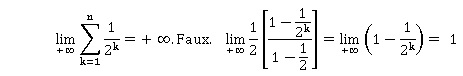
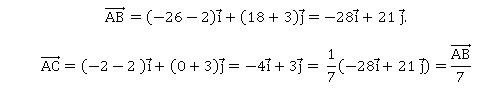
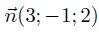 .
.