Mathématiques,
Groupe B Bts 2019.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
......
.....
|
Exercice 1.
10 points.
Lorsqu’un
fil électrique est parcouru par un courant électrique d’intensité
constante, celui-ci s’échauffe par effet Joule et sa température varie
en fonction du temps. On note f (t ) la température, exprimée en degré
Celsius, du conducteur à l’instant t , exprimé en seconde, avec t
variant dans l’intervalle [0 ; +∞[.
Dans cet exercice, on se propose d’étudier l’évolution de la température du conducteur en fonction du temps.
Les trois parties de cet exercice peuvent être traitées de façon indépendante
A. Résolution d’une équation différentielle.
À l’instant t = 0 de la mise sous tension, la température du conducteur
est celle du milieu ambiant, c’est-à-dire 18 degrés Celsius. Ainsi, on
a f (0)) = 18.
Dans les conditions de l’expérience, la fonction f est solution de l’équation différentielle (E) :
y′ +0,05y = 2,
où y est une fonction inconnue de la variable t , définie et dérivable sur l’intervalle [0 ; +∞[, et y′ sa fonction dérivée.
1. a. Résoudre l’équation (E0) : y′ +0,05y = 0.
y = A e-0,05 t avec A une constante.
b. Vérifier que la fonction g définie par g (t ) = 40 est une solution de l’équation différentielle (E).
g'(t) = 0 ; 0,05 x40 = 2.
c. En déduire les solutions définies sur l’intervalle [0 ; +∞[ de l’équation différentielle (E).
f(t) = Ae-0,05 t +40.
2. On rappelle que la température initiale du conducteur est 18° Celsius.
Ainsi, la fonction f exprimant la température du conducteur est la
solution de l’équation différentielle (E) vérifiant la condition
initiale f (0) = 18. Déterminer alors une expression de la fonction f .
f(0) = 18 = A +40 ; A = -22.
f(t) = 40 -e-0,05 t .
B. Étude de la fonction f.
On admet que la fonction donnant la température du conducteur est la fonction f définie sur [0 ; +∞[
par : f (t )= −22e−0,05t +40.
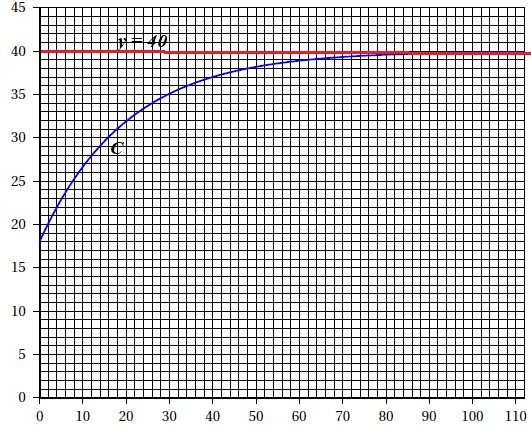
On note C la courbe représentative de la fonction f dans le plan muni d’un repère orthogonal.
La courbe C est tracée.
1. a. On admet que la limite en plus l'infini de e-0,05t est nulle.
Déterminer alors la limite de la fonction f en +∞.
La limite de f(t), quand x tend vers plus l'infini, est égale à 40.
b. En déduire que la courbe C admet une asymptote dont on donnera une équation.
Tracer cette asymptote sur la représentation graphique donnée..
La droite d'équation y= 40 est asymptotr à C.
2. Un logiciel de calcul formel permet d’obtenir ci-dessous une expression de la dérivée f ′ de la fonction f .
f '(t) = 1,1 exp-0,05t.
a. En admettant ce résultat, étudier les variations de la fonction f sur [0 ; +∞[.
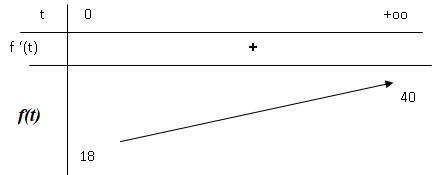
b. Dresser le tableau de variation de f sur [0 ; +∞[.
La dérivée est strictement positive ; la fonction f est strictement croissante sur [0 ; +∞[..
3. Ce même logiciel
de calcul formel affiche la partie régulière du développement limité à
l’ordre 2 de la fonction f au voisinage de zéro.
-18 +1,1t-11 /400 t2.
Les deux questions suivantes sont des questions à choix multiples. Une seule réponse est exacte.
Recopier sur la copie la réponse qui vous parait exacte. On ne demande aucune justification.
La réponse juste rapporte 0,5 point. Une réponse fausse ou une absence de réponse ne rapporte ni n’enlève de point.
a. Une équation de la tangente T à la courbe C au point d’abscisse 0 est :
y = 18 ; y = 18 +1,1t ; y = 18 +1,1t -11t2 /400.
b. La vitesse de chauffe, exprimée en degré Celsius par seconde, à l’instant initial est égale à
f ′(0). Cette vitesse vaut :
18 ; 1,1 ; 11 / 400.
C. Dépassement d’un seuil et algorithmique.
On cherche à déterminer le premier instant t , en seconde, à partir
duquel la température du fil du conducteur dépasse 21°Celsius.
À cette fin, on considère l’algorithme suivant.
t ←0
Tant que f (t ) < 21
t ←t +1
Fin de Tant que
Remarque : dans cet algorithme t ←0 signifie que t prend la valeur 0.
1. Faire tourner cet algorithme « à la main » en complétant le tableau..
Valeur de t
|
Valeur de f(t) arrondie à 10-2
|
Condition f(t) < 21
|
0
|
18
|
vraie |
1
|
19,07
|
vraie
|
2
|
20,09
|
vraie
|
3
|
21,06
|
faux
|
2. Quelle sera la
valeur contenue dans la variable t à la fin de l’algorithme ?
Interpréter ce résultat dans le contexte de l’exercice.
Au bout de 3 s, la température dépasse 21°C.
|
...
|
|
Exercice 2. 10 points..
Les trois parties de cet exercice peuvent être traitées de façon indépendante.
Dans cet exercice, sauf mention du contraire, les résultats approchés sont à arrondir à 10−3.
Un grand constructeur d’engins de travaux publics sous-traite la fabrication de chenilles et de pneumatiques à deux entreprises.
A. Événements indépendants.
Dans la première entreprise, les pneumatiques produits sont soumis à un
contrôle de qualité constitué de deux tests. On prélève au hasard un
pneumatique après contrôle. On considère les évènements suivants :
A : « le pneumatique a validé le premier test » ;
B : « le pneumatique a validé le second test ».
Un pneumatique est dit conforme s’il a validé les deux tests.
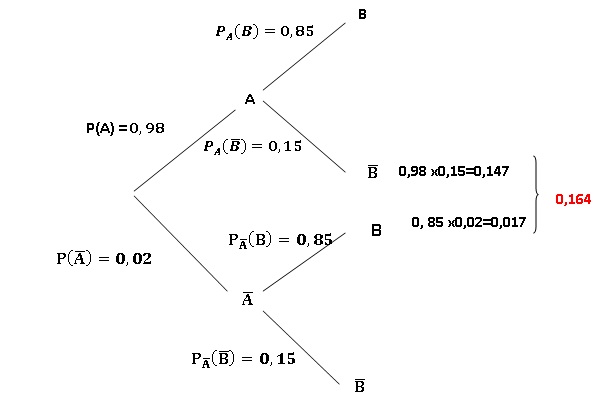
Une étude statistique permet d’admettre que les probabilités des
évènements A et B sont respectivement P(A) = 0,98 et P(B) = 0,85 et que
les évènements A et B sont indépendants. Calculer les probabilités des
évènements suivants :
1. E1 : « le pneumatique contrôlé est conforme » ;
P(A) x P(B) = 0,98 x0,85 =0,833.
2. E2 : « le pneumatique contrôlé n’est pas conforme » ;
P(E2) = 1 -0,833 =0,167.
3. E3 : « le pneumatique n’a validé qu’un seul des deux tests. ».
B. Loi exponentielle.
Dans la seconde entreprise, fabriquant les chenilles, une machine est
chargée d’assembler le barbotin moteur des chenilles. Le barbotin
moteur est la roue dentée, à une ou deux rangées de dents, qui entraîne
la chenille.
Cette machine nécessite d’être étalonnée très régulièrement. La durée
de bon fonctionnement entre deux étalonnages, exprimée en heure, de
cette machine est modélisée par une variable aléatoire T de loi
exponentielle de paramètre l..
1. Pour cette machine, l’entreprise a constaté que la durée moyenne de bon fonctionnement est 10 heures.
Montrer que ¸ l = 0,1.
l = 1 / E(T) = 1 / 10 = 0,1 h-1.
2. a. Calculer P(T < 20).
P(T < 20)=1- exp(-0,1 x20) = 0,865.
b. Déterminer la probabilité que la durée de bon fonctionnement de cette machine dépasse 15 heures.
P(T > 15) = exp(-0,1 x15) = 0,223.
3. Déterminer la durée médiane de bon fonctionnement, c’est-à-dire la valeur t0 telle que : P (T < t0) = 0,5.
0,5 = 1 -exp(-0,1 t0) ; 0,5 = exp(-0,1 t0) ; -ln(2) = -0,1 t0 ; t0 = 10 ln(2) ~6,9 h.
|
....
|
C. Intervalle de confiance.
Pour assurer la suspension de l’engin, de nombreux systèmes peuvent
être utilisés : des balanciers, des bras oscillants, des ressorts à
lames ou hélicoïdaux ou encore des suspensions hydropneumatiques.
Dans cette partie, on s’intéresse à la fabrication de ressorts
hélicoïdaux. On souhaite estimer la proportion p de ressorts conformes
dans l’ensemble de la production. Pour cela on prélève au hasard un
échantillon de 50 ressorts parmi cette production (celle-ci est
suffisamment importante pour que l’on puisse assimiler ce prélèvement à
un tirage avec remise).
On constate que 44 ressorts de cet échantillon sont conformes aux normes fixées par le cahier des charges.
1. Donner une
estimation ponctuelle f de la proportion inconnue p des ressorts qui
sont conformes aux normes dans l’ensemble de la production.
f =44 / 50 = 0,88.
2. Soit F la
variable aléatoire qui à tout échantillon de 50 ressorts ainsi prélevé,
associe la fréquence, dans cet échantillon, des ressorts conformes. On
suppose que F suit la loi normale de moyenne p inconnue et d’écart type
[ p(1-p) / n ]½.
a. Déterminer un intervalle de confiance centré sur f de la proportion p au niveau de confiance e 95%.
1,96 [f (1-f) / n ]½ = 1,96 (0,88 x0,12 / 50 )½ =0,090.
Intervalle de confiance [ 0,88 -0,090 ; 0,88 +0,090) soit [0,79 ; 0,97 ].
b. Peut-on affirmer que p est compris dans cet intervalle de confiance? Pourquoi ?
Par définition p appartient à cet intervalle de confiance..
|
|