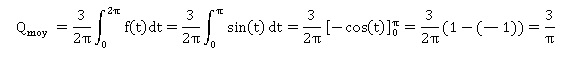Mathématiques, Groupe A Bts 2019.

Mathématiques, Groupe A Bts 2019.
Electrotechnique, systèmes phoniques, techniques physiques pour l'industrie et le laboratoire.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

.
.

......

.....

Exercice 1. 12 points.
Les parties A et B sont indépendantes
Partie A.
On étudie, dans cette partie, le débit d’une pompe à trois pistons alimentant un bac de stockage;
On note f la fonction périodique de période 2p définie par :
f (t ) = sin(t ) si 0 < t < p.
0 si p < t < 2p.
1. Les débits q₁, q₂, q₃ de chacun des trois pistons (exprimés en litre par seconde) sont donnés, à l’instant t (exprimé en seconde), par : q₁(t )= f (t ) ; q₂(t )= f (t +2p/3) ; q₃(t )= f (t +4p/3).¶.
Voici les représentations graphiques sur l’intervalle [−2p ; 2p] des fonctions q₁, q₂ et q₃ dans le désordre.
Associer chaque courbe à la fonction, q₁, q₂ ou q₃ qu’elle représente. Justifier brièvement.

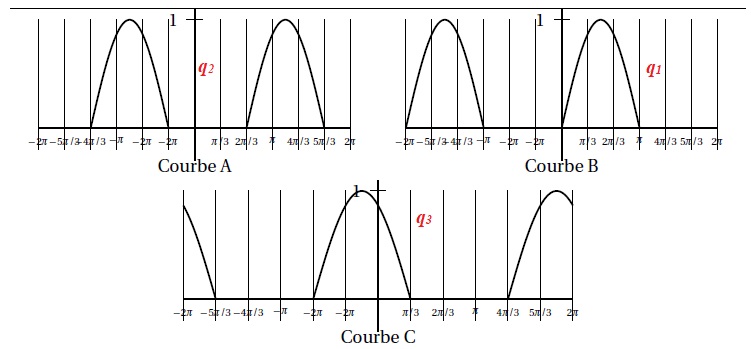
q₁ est nul sur l'intervalle p < t < 2p.
q₂ : décalage de 2p/3 vers la droite ( 2 carreaux) par rapport à q₁.
q₃ : décalage de 4p/3 vers la droite (4 carreaux ) par rapport à q₁.
2. Le débit en litre par seconde, de la pompe à trois pistons est donné par :
Q(t )= q₁(t )+q₂(t )+q₃(t ).
a. Calculer Q(0) et Q (p/3). Écrire le détail des calculs.
q₁(0) = sin (0) = 0 ; q₂(0) = sin (0+2p/3) = 3^½ / 2 ; q₃(0) = f (0+4p/3) =0.
Q(0) = 3^½ /2~0,866 L s^-1.
q₁(p/3) = sin (p/3) = 3^½ / 2 ; q₂(p/3) =f(p) = 0 ; q₃=(p/3) = f (5p/3) =0.
Q(p/3) =3^½ /2 ~ 0,866 L s^-1.
On donne pour la suite : Q(p/6) = 1 ; Q(p/2) =1 ; Q(2p/3) = 3^½/2.
b. Montrer que Q (t+2p/3)= Q(t) pour tout réel t . En déduire une période de Q.
q₁ =f(t+2p/3) = q₂(t) ; q₂ =f(t+4p/3) = q₃(t) ; q₃ =f(t+6p/3) = q₁(t) ;
Q (t+2p/3)= Q(t), fonction de période 2p/3.
c. On admet que Q est dérivable sur ]0 ; p/3] u ]p/3 ; 2p/3[.
On donne ci-dessous la représentation graphique de la fonction dérivée de Q sur cet ensemble.

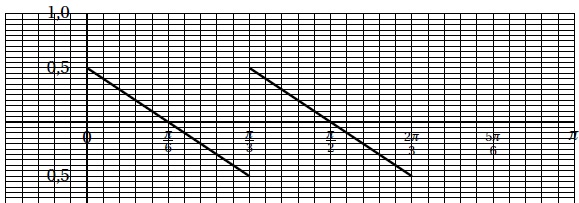
Recopier et compléter, à l’aide du graphique ci-dessus. le tableau de variations de la fonction Q sur l’intervalle [0 ; 2p/3]
. On y reportera les valeurs calculées, ou données au a.

3. On appelle taux d’irrégularité du débit de la pompe le nombre : q =(Q_M-Q_m) / Q_moy, où Q_M est le débit maximum de la pompe sur une période, Q_m est le débit minimum de la pompe sur une période et Q_moy est le débit moyen de la pompe.
On admet que :

...

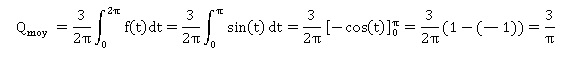
Partie B.
1. L’entreprise qui gère les bacs de stockage fait contrôler les pompes sur différents sites.
20% des pompes sont sous garantie.
Le technicien constate que :
• 1% des pompes sous garantie sont en panne;
• 10% des pompes qui ne sont plus sous garantie sont en panne.
On tire au hasard, dans le fichier de l’entreprise, la fiche d’une pompe dont l’entreprise assure le contrôle.
On considère les évènements suivants :
G : « la pompe est sous garantie » et D : « la pompe est en panne ».
a. Construire un arbre pondéré qui modélise la situation.
b Démontrer que : P(D) = 0,082.
c. Le technicien affirme que moins de 2% des pompes en panne sont sous garantie. Le technicien a t-il raison ?

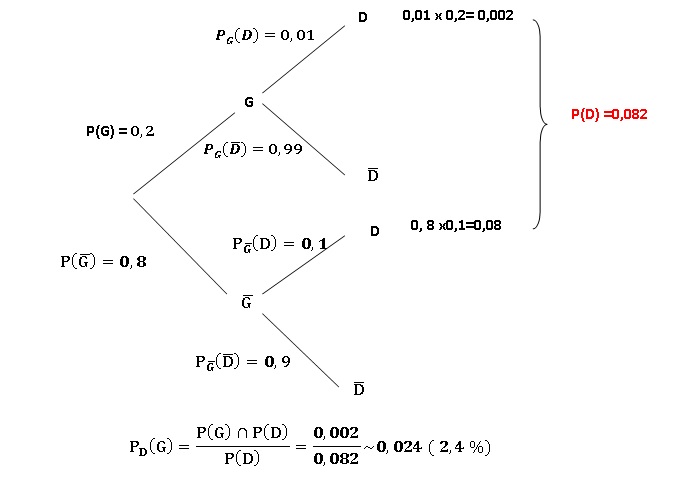
2,4 % des pompes en panne sont sous garantie. Le technicien a tord.
2. On tire au hasard 50 fiches de pompes dans le fichier de l’entreprise. On assimile ce prélèvement à un tirage avec remise.
On note X la variable aléatoire qui, à tout prélèvement de 50 fiches, associe le nombre de fiches de pompes en panne.
On rappelle que la probabilité qu’une pompe soit en panne est 0,082.
a. Justifier que la variable aléatoire X suit une loi binomiale dont on précisera les paramètres.
Les prélevements sont indépendants et leur nombre est fixé à n = 50.
Chaque tirage peut déboucher seulement sur 2 résultats : la probabilité qu'une pompe soit en panne est constante p = 0,082. La probabilité qu'une pompe ne soit pas en panne est q = 1-p = 0,918.
La loi binomiale B(n=50, p = 0,082) est valide
b. Calculer la probabilité que, parmi les 50 fiches tirées, il y ait exactement deux fiches de pompes en panne. Arrondir au millième.
P(X=2) = 0,136.
c. Calculer la probabilité que parmi les 50 fiches tirées, il y ait plus de deux fiches de pompes en panne. Arrondir au millième.
P(X > 2) = 1- P(X < 2) = 1-0,211 = 0,789.
d. Calculer l’espérance de la variable alêatoire X et interpréter ce résultat.
E = np = 50 x0,082 = 4,1.
En moyenne, il y a 4 pompes en panne.

....

Exercice 2. ( 8 points).
On considère le bac de stockage cylindrique représenté ci-dessous.

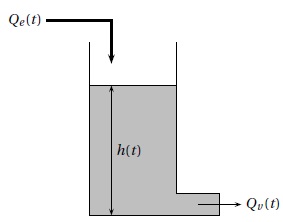
À l’instant t , en seconde (s), on note h(t ) la hauteur d’eau, en mètre (m), dans le bac, Q_e (t ) le débit d’entrée, en m³s⁻¹, et Q_v (t ) le débit de vidange, en m³s⁻¹.
À l’instant t = 0, le bac est vide, donc : h(0) = 0.
La conservation de la matière permet d’écrire, pour tout t >0 :
Q_e (t )= Sh′(t )+Q_v (t )
où S est l’aire de la base du bac, exprimée en m², et h′ la fonction dérivée de h.
Dans l’exercice, on a S = 8 m².
De plus on suppose, en faisant une approximation, que : Q_v(t ) = 2h(t ).
On a donc : 8h'(t) +2h(t) =Q_e(t).
On veut que la hauteur d’eau h(t ) atteigne 10 cm, soit 0,1m. Pour cela, on agit sur le débit d’entrée Q_e (t ).
Partie A.
Dans cette partie. on suppose que pour t >0 : Q_e (t )= 0,2.
La fonction h est donc solution sur l’intervalle [0 ; +∞[ de l’équation différentielle : 8y′ +2y = 0,2 (E)
1. a. Donner les solutions sur l’intervalle [0 ; +∞[ de l’équation différentielle : 8y′+2y = 0 (E₀).
y = A exp(-0,25t)
b. Déterminer une solution particulière constante y₀ de l’équation différentielle (E).
y₀= 0,1.
c. Donner les solutions sur l’intervalle [0 ; +∞[ de l’équation différentielle (E).
y = A exp(-0,25t) +0,1.
2. L’une des quatre expressions ci-dessous est celle de h(t ), pour tout réel t >0. Laquelle? Justifier la réponse.
h(t ) = −0,1e^−0,25t +0,2 ; h(t ) = −0,1e^−4t +0,1 ; h(t ) = -e^−0,25t +0,1 ; h(t ) = −0,2e^−0,25t +0,1.
A l'instant t = 0, h(0) = 0 ; 0 = A +0,1 ; A = -0,1. ; h(t) = 0,1 -0,1 exp(-0,25t).
Aucune des expressions précédentes n'est correcte.

Partie B.
On souhaite obtenir plus rapidement la hauteur de 10 cm d’eau dans le bac.
Pour cela, on modifie le débit d’entrée. On prend désormais pour tout réel t >0 : Q_e (t )=U(t )−0,8U(t −0,9)
où U désigne la fonction échelon unité : U(t )= 0 si t < 0 et 1 si t >0
h vérifie donc, pour tout réel t >0 : 8h′(t )+2h(t ) =U(t )−0,8U(t −0,9) (E).
De plus, on rappelle que h(0) = 0.
1. Représenter sur la copie Q_e (t ) en fonction de t , pour t >0.

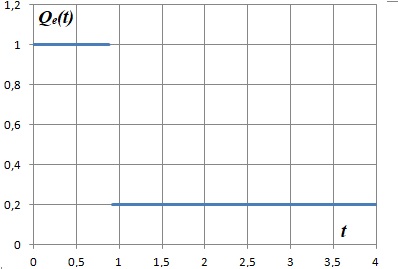
2. On note H la transformée de Laplace de h.
a. Écrire l’égalité obtenue en appliquant la transformation de Laplace aux deux membres de l’égalité (E).
b. Montrer que H(p) =[ 1−0,8e^−0,9p] / [(2+8p)p].
L(h'(t)) = pH(p)-h(0⁺) = pH(p).
8pH(p) +2H(p) = 1 / p -0,8 / p e^-0,9p.
(8p+2) H(p)=(1-0,8e^-0,9p) / p.
(8p+2)p H(p)=1-0,8e^-0,9p.
.H(p) =[ 1−0,8e^−0,9p] / [(2+8p)p]
3. On note : A(p)= 1/ [(2+8p)p ].
a. Vérifier que : A(p)= 0,5 / p − 4 / (2+8p).
. 0,5 / p − 4 / (2+8p) =[ 0,5( 2+8p) -4p ] / [p(2+8p)] =(1+4p-4p) / [p(2+8p)] =1/ [(2+8p)p ].
b. Comme 4 /(2+8p) =0,5 /(p +0,25) on a aussi : A(p)=0,5 / p -0,5 /(p+0,25).
En déduire l’original a(t ) de A(p).
a(t) = 0,5 U(t) -0,5 e^-0,25t.U(t).
c. On remarque que : H(P) = A(p)×(1−0,8e^−0,9p )= A(p)−0,8A(p)e^−0,9p.
Déterminer une expression de h(t ) pour tout réel t >0.
h(t) = L^-1(A(p) -0,8 L^-1[A(p) e^-0,9p]. Dans le terme [A(p) e^-0,9p on reconnaît un retard de 0,9. Son original est a(t-0,9) U(t-0,9).
Par suite h(t) = a(t) U(t) -a(t-0,9) U(t-0,9).
Remplacer a(t) par son expression :
h(t) = 0,5 U(t) -0,5 e^-0,25t.U(t) -0,9 x 0,5[ U(t-0,9) - e^-0,25(t-0,9).U(t-0,9)

4. La courbe représentative de la fonction h est tracée ci-dessous

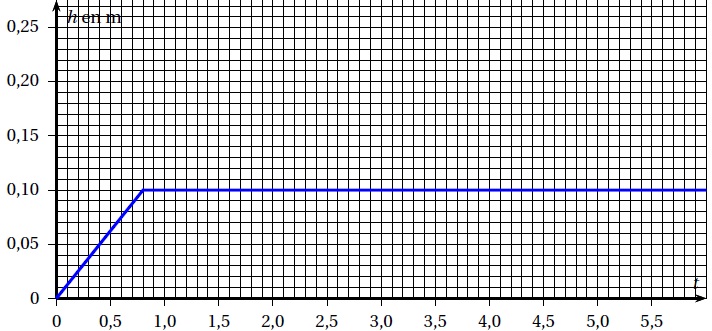
Estimer graphiquement le gain de temps réalisé pour atteindre la hauteur de 10 cm si l’on remplace le débit d’entrée de 0,2 m³s⁻¹ (étudié dans la partie A) par le débit de la partie B.
Partie B : 10 cm sont atteints en 0,8 s.
Partie A : 10 cm sont atteints en un temps supérieur à plus de 10s.
.

.

menu