Sous-marin "SAGA", BTS Fluides, énergies, domotique 2019.

Sous-marin "SAGA", BTS Fluides, énergies, domotique 2019.
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

.
.

......

.....

A. Immersion du sous-marin.
On souhaite trouver l’épaisseur minimale de la vitre du hublot du sous-marin.
Données :
• Pression atmosphérique : P_atm = 1,0⋅10⁵ Pa
• Masse volumique de l’eau de mer à la surface : ρ = 1,03⋅10³ kg⋅m^-3
• Champ de pesanteur terrestre : g = 9,81 m⋅s^-2
• Masse du sous-marin lors des déplacements en plongée : M_T = 550 t
• Longueur du sous-marin : L = 28 m
• Rayon du sous-marin : R = 7,0 m
• Diamètre du hublot : d = 50 cm
On suppose que l’eau de mer est incompressible et homogène, c’est-à-dire que sa masse volumique ρ est constante. On note P₀ la pression de l’eau de mer en surface, c’est-à-dire à la côte z égale à 0.
1. Donner l’expression de la pression P(z) à la côte z en fonction de ρ, g, z et P₀.
P(z) = P₀ +r g z.
2. Vérifier que la pression P₆₀₀ à la profondeur de 600 m est égale à 6,2⋅10⁶ Pa.
P600 = 1,0 10⁵ +1,03 10³ x9,81 x600 ~6,2⋅10⁶ Pa.
3. Calculer la valeur maximale F_max de la force que doit supporter le hublot du sous-marin.
Surface du hublot : S = p D² / 4 = 3,14 x0,50² /4 =0,196 m².
F_max= P₆₀₀ S =6,2 10⁶ x0,196 ~1,2 10⁶ N =1,2 10³ kN.
4. À l’aide du document, indiquer l’épaisseur minimale emin de la vitre du hublot.
Tableau de valeur pour un hublot cylindrique de diamètre 50 cm :

épaisseur e ( cm)
pression P ( 10⁵) Pa
force F(kN)

2
4,0
78

4
15,9
312

6
35,8
702

8
63,7
1250

10
99,5
1950

..

...

B. Régulation de température.
Afin de contrôler les températures dans les différents compartiments du sous-marin, des sondes de température d’ambiance sont installées. Le capteur de température de ces sondes est une Pt100, c’est une résistance dont la valeur varie avec la température.
1. Indiquer les grandeurs d’entrée et de sortie de la sonde.
Grandeur d'entrée : température ; grandeur de sortie : résistance électrique.
2. Décrire le protocole expérimental permettant de tracer la courbe caractéristique de ce capteur.
Un protocole expérimental propose de plonger une sonde de platine et un thermomètre à alcool ( supposé correctement étalonné ) dans un ballon contenant de l'eau. Un chauffe ballon permet d'élever progressivement la température de l'eau et un ohmmètre est utilisé pour mesurer la résistance de la sonde de platine.
3. Tracer la courbe caractéristique de la sonde Pt100 dans le domaine de température 0 °C à 300 °C : R = f(θ).
4. En déduire l’expression de la résistance R en fonction de la température θ.

....

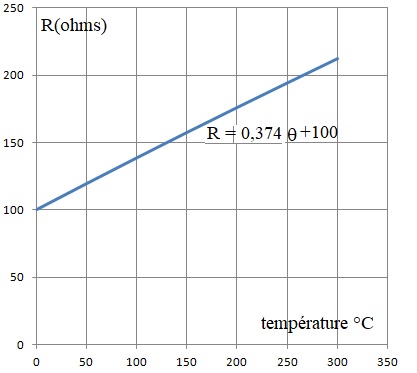
C. Propulsion du sous-marin.
Les systèmes de propulsion doivent répondre à quelques grandes exigences, en particulier fonctionner de manière anaérobie, c’est-à-dire sans utiliser d’air, car en immersion totale le milieu extérieur est l’eau et non l’air. SAGA est équipé de deux moteurs Stirling qui fournissent en plongée la puissance nécessaire à la propulsion et à l'alimentation électrique. Ils produisent également la chaleur utilisée pour le chauffage du compartiment hyperbare ainsi que la protection contre le froid des plongeurs pendant leurs sorties en scaphandre.
Le développement, l'industrialisation et la commercialisation du moteur Stirling pour la propulsion marine, ont été entrepris depuis les années 1970 en Suède par la société United Stirling maintenant intégrée au chantier naval Kockums à Malmö.
Le fluide de travail décrit le cycle constitué des quatre phases suivantes :
On étudie le cycle de Stirling idéal au cours duquel n moles de gaz parfait de rapport g subissent un cycle à quatre phases, dit aussi cycle à quatre temps. On rappelle : g = Cp / Cv..
1er temps : compression isotherme de l’état 1 à l’état 2. T_froide= T₁ = 300 K ; P₁ = 1,0 bar.
2ème temps : échauffement isochore de l’état 2 à l’état 3.
3ème temps : détente isotherme de l’état 3 à l’état 4. T_chaude= T₃ = 600 K.
4ème temps: refroidissement isochore de l’état 4 à l’état 1.
Il n’y a pas de travail autre que celui des forces de pression. On rappelle que Cv = R / (g-1).
Lors d’une transformation :
• isotherme d’un état A à un état B, le transfert thermique est Q_AB= n∙R∙T∙ ln (V_B /V_A).
• isochore d’un état A à un état B, le transfert thermique est Q_AB = n∙Cv ∙ (T_B-T_A).
On souhaite calculer le rendement du moteur Stirling.
1. Représenter l’allure du cycle dans le diagramme (P,V) et orienter le cycle.

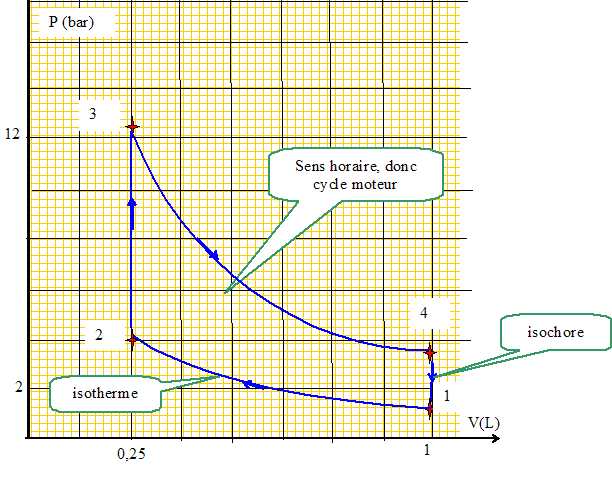
2. Exprimer les transferts thermiques Q₁₂, Q₂₃, Q₃₄ et Q₄₁ échangés par le fluide au cours du cycle.
Isotherme : Q₁₂= n∙R∙T₁∙ ln (V₂ /V₁).
Isochore : Q₂₃= n∙Cv ∙ (T₃-T₂).
Isotherme : Q₃₄= n∙R∙T₃∙ ln (V₄ /V₃) = n∙R∙T₃∙ ln (V₁ /V₂) = - n∙R∙T₃∙ ln (V₂ /V₁)
Isochore : Q₄₁= n∙Cv ∙ (T₁-T₄) =n∙Cv ∙ (T₂-T₃) =-n Cv ∙ (T₃-T₂).
L'énergie d'un gaz parfait ne dépend que de la température. Au cours d'une transformation isotherme, l'énergie interne du gaz parfait ne varie pas.
DU₁₂ = 0 ; DU₁₂ =W₁₂ +Q₁₂ d'où Q₁₂ = -W₁₂.
DU₃₄ = 0 ; DU₃₄ =W₃₄ +Q₃₄ d'où Q₃₄ = -W₃₄.
Les travaux sont nuls au cours des transformations isochores. W₂₃=W₄₁=0.
3. À l’aide du premier principe de la thermodynamique, exprimer le travail du cycle W_cycle.
W_cycle+Q₁₂ + Q₂₃+ Q₃₄ + Q₄₁=0.
W_cycle= -(Q₁₂ + Q₂₃+ Q₃₄ + Q₄₁)= W_{12 +}W₃₄= - (Q₁₂ +Q₃₄)
4. Pour un moteur, le rendement est défini par la valeur absolue du rapport du travail échangé au cours du cycle par la quantité de chaleur reçue au cours du cycle. Donner l’expression du rendement η du moteur et vérifier qu’il peut s’exprimer en fonction des températures T₁ et T₃ selon la relation h= (T₃-T₁) / T₃.
h=énergie utile / énergie dépensée =| W_cycle/ Q₃₄ |= - (Q₁₂ +Q₃₄) / Q₃₄ .
Q₁₂ +Q₃₄= n∙R∙T₁∙ ln (V₂ /V₁) - n∙R∙T₃∙ ln (V₂ /V₁) = n∙R (T₁∙ -T₃) ln (V₂ /V₁).
- (Q₁₂ +Q₃₄) = n∙R (T₃∙ -T₁) ln (V₂ /V₁).
Q₃₄ = - n∙R∙T₃∙ ln (V₂ /V₁).
h=(T₃-T₁) / T₃.
5. Calculer la valeur du rendement.
h = (600-300) / 600 = 0,50.

D. Protection de la coque.
« La protection cathodique permet de protéger un métal contre la corrosion. Pour modifier le potentiel du métal à protéger cathodiquement, une anode installée dans le même électrolyte est utilisée. Les anodes peuvent être de deux types : soit des anodes ayant un potentiel plus électronégatif que le métal à protéger (anode sacrificielle), soit des anodes couplées à un générateur de tension continue imposant une différence de potentiel entre les deux métaux (méthode à courant imposé). Dans la protection cathodique de l'acier ou de métaux ferreux (par exemple sur les coques de bateaux et arbres d'hélice...) par anodes sacrificielles, le zinc est souvent choisi pour son électropositivité (Zn²⁺), sa facilité de moulage et sa bonne réactivité en milieu agressif. »
Source Wikipédia
1. Le texte issu de Wikipédia semble manquer de rigueur scientifique. Reformuler la phrase suivante : le zinc est souvent choisi pour son électropositivité (Zn2+) dans la protection cathodique de l'acier ou de métaux ferreux.
Le zinc est plus réducteur que le fer. Il s'oxyde à la place du fer ; ce dernier est protégé de la corrosion.
2. On donne le dispositif expérimental :

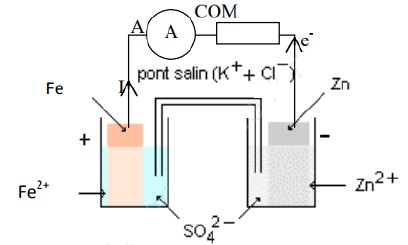
À partir du dispositif expérimental donné précédemment, écrire les deux demi-équations électroniques observées à l’anode et à la cathode.
Données : couples rédox : Fe²⁺/Fe et Zn²⁺/Zn.
Oxydation du zinc à l'anode : Zn = Zn²⁺ + 2e^-.
Réduction de Fe²⁺ à la cathode : Fe²⁺ + 2e^- = Fe.
II. Étude cristallographique du fer.
Le fer cristallise en un réseau cubique centré « C.C ».
Données :
Masse molaire atomique : M (Fe) = 55,8 g⋅mol^-1
Rayon atomique d’un atome de Fe : R = 124,0 pm
Nombre d’Avogadro : N_A = 6,02.10²³ mol^-1
Une maille est le motif géométrique le plus simple, qui en se répétant indéfiniment, constitue un réseau cristallin.

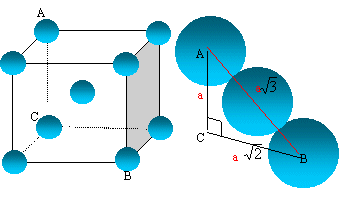
1. Vérifier que la population N d’une maille est égale à deux.
Les atomes des sommets apartiennent à 8 mailles et comptent pour 1/8 ; 1 atome central.
8(1/8) + 1 = 2
2. Montrer que la valeur de la masse volumique ρ_Fe du fer est égale à 7,89.10³ kg∙m^-3.
Arète de la maille : a = 4 R / 3^½ =4 x124 /3^½= 286 pm=2,86 10^-10 m.
Volume d'une maille : V=a³ = 2,34 10^-29 m³.
Masse de la maille : m=2 x 55,8 10^-3 / (6,02 10²³) =1,85 10^-25 kg.
Masse volumique : m / V = 1,85 10^-25 / (2,34 10^-29)=7,9.10³ kg∙m^-3.
3. La coque du sous-marin, constituée uniquement de fer, peut être modélisée par un cylindre de volume V égal à 15,4 m³.
Sa masse représente 22% de la masse totale du sous-marin.
Retrouver la masse M_T totale du sous-marin.
Masse de fer : 15,4 x7,89 10³ =1,21 10⁵ kg = 121 tonnes.
121 /0,22 ~550 tonnes.

menu