Principe
des capteurs inductifs,
Bts Métiers de l'eau 2017.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
......
.....
|
Partie 3 – Principe physique des capteurs
inductifs (4,5 points)
Les capteurs inductifs sont couramment utilisés pour détecter la
présence d’éléments métalliques (ferreux ou non ferreux) dans les environnements difficiles
tels que les effluents corrosifs, rejetés dans l’industrie du tannage des peaux.
La méthode de détection peut s'appuyer sur la variation de l'inductance
d'une bobine à l'approche d'un métal. En effet, l'inductance augmente si on approche
de la bobine un objet ferromagnétique (fer ou acier par exemple), alors qu'elle diminue en
l’absence de fer.
1. Modélisation de la variation de l’inductance de la bobine
On dispose d’une bobine portant les indications : L = 0,20 H ; r = 5,0 ohms.
On réalise le montage suivant afin de tester le comportement de la
bobine :
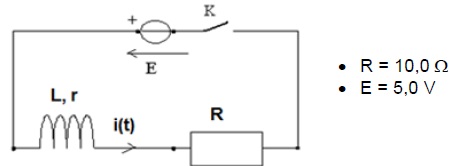
On ferme l’interrupteur et on enregistre l’évolution de la tension uR aux
bornes du conducteur ohmique de résistance R en fonction du temps (voir
courbes ci-après).
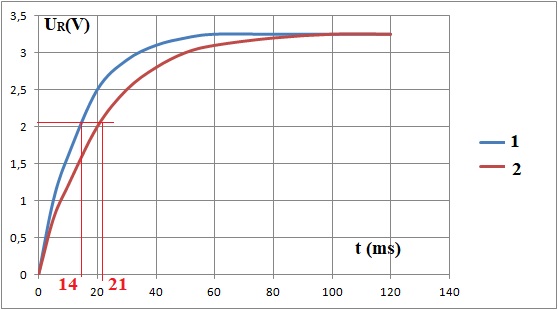
L’expérience est faite, tout d’abord sans métal, à proximité de la
bobine (courbe 1), puis en présence d’une pièce en fer (courbe 2 ) :
1.1. Expliquer pourquoi l’évolution temporelle de uR est aussi celle de l’intensité i du courant.
La tension aux bornes d'un conducteur ohmique est proportionnelle à l'intensité du courant.
1.2. L’équation différentielle régissant l’évolution temporelle de l’intensité du courant dans la bobine est :
Ldi /dt +(R+r)i = E
1.2.1. Écrire cette équation différentielle en régime permanent au cours duquel l’intensité est constante.
di /dt = 0 ; i = E /(R+r).
1.2.2. En déduire la valeur de cette constante.
i = 5,0 / (10 +5) = 5 / 15 =1 / 3 ~0,33 A.
1.3. Déterminer la valeur de la constante de temps du circuit : t1 pour la courbe (1) et t2 pour la courbe (2).
On rappelle que la constante de temps correspond à 63 % de la valeur de i(t) en régime permanent.
t1 ~14 ms ; t2 ~21 ms.
1.4. En déduire les valeurs L1 et L2
de l’inductance dans chaque cas. Vérifier que l'inductance augmente
bien quand on approche de la bobine un objet ferromagnétique.
t1 =L1 /(R+r) ; L1 =15 x 0,014 ~ 0,21 H ; L2 =15 x 0,021 ~ 0,31 H.
|
...
|
|
.
|
....
|
2. L’oscillateur
Le détecteur est équivalent à un oscillateur constitué d'un condensateur et d'une bobine.
Du fait de la variation de l'inductance de la bobine, l'oscillateur voit sa fréquence modifiée.
Un montage électronique permet alors de comparer la fréquence de cet
oscillateur à une fréquence fixe. La comparaison indique ainsi la
présence d'un métal et sa nature. L'oscillateur, utilisé dans le
détecteur, est équivalent à un oscillateur électrique non amorti,
constitué par un condensateur de capacité C et une bobine d’inductance
L égale à 0,22 H et de résistance nulle.
Le système est ainsi en résonance à une fréquence f0.
On rappelle l’expression de la période propre de l’oscillateur : T0 = 2 p (LC)½.
Calculer la capacité C du condensateur pour que la fréquence propre f0 soit égale à 2,0 kHz en absence de métal à proximité.
T0 = 1 / 2000 =5,0 10-4 s.
T02 = 4 p2 LC ; C = T02 /( 4 p2 L)=25 10-8 /(4 x3,142 x0,22) ~2,9 10-8 F.
|
|

