L'accident
de Tchhernobyl, 30 ans plus tard,
Bts Métiers de la chimie 2017.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
......
.....
|
Lorsque
le 26 avril 1986, le
réacteur n°4 de la centrale de Tchernobyl en Ukraine explose,
l'humanité connaît alors la plus grave catastrophe nucléaire civile
jamais enregistrée dans le monde.
Une explosion et un incendie se produisent. Dans le coeur, les crayons
de combustible se fragmentent. Surchauffés, ils explosent et provoquent une déflagration
qui soulève la dalle supérieure du réacteur, d'une masse de 2000 tonnes. La partie
supérieure du coeur du réacteur est à l'air libre. Une seconde explosion, due probablement à du
dihydrogène, se produit alors : le graphite prend feu. Trente foyers s'allument. Il faudra trois heures
aux pompiers pour les éteindre. En l'absence d'enceinte de confinement, les débris
radioactifs du coeur du réacteur (iode 131, césium 134 et 137, ruthénium 103 et 106), dont certains sont
très volatils, sont libérés
dans l'environnement.
L'accident majeur de Tchernobyl vient d'avoir lieu : il est de niveau
sept sur l'échelle INES (International Nuclear Event Scale) qui en compte... sept.
Dans ce problème, on se propose d’analyser l’impact sur l’environnement
30 ans plus tard de deux « débris » radioactifs produits lors de la catastrophe de
Tchernobyl.
1. Au coeur du réacteur.
Dans une centrale nucléaire à neutrons lents, le combustible est
l’uranium enrichi ; il contient 3% d’uranium 235 fissile et 97%
d’uranium 238 non fissile.
1.1. Donner la composition des noyaux 23592 U et 23892U.
23592 U : 92 protons et 235-92 = 143 neutrons.
23892U : 92 protons et 238-92 = 146 neutrons.
1.2. Quelle relation lie ces noyaux ? Justifier.
Ces noyaux ne diffèrent que par leurs nombres de neutrons : ils sont isotopes.
2. Impact de l’iode 131.
Lors de l’impact d’un neutron sur un noyau d’uranium 235, plusieurs
réactions de fission sont possibles. La plus fréquente conduit à des
noyaux de zirconium 95 et de tellure 138 ainsi qu’à un nombre k de
neutrons.
2.1. Ecrire l’équation de la réaction de fission. Déterminer la valeur de k et le numéro atomique du tellure. Justifier.
23592 U +01n ---> 9540 Zr + 138Z Te +k 01n.
Conservation de la charge : 92 = 40 +Z ; Z = 52.
Conservation du nombre de nucléons : 235 +1 = 95 +138 +k ; k =2.
2.2. Expliquer pourquoi la réaction de fission peut « s’emballer ».
La réaction produit plus ne neutrons qu'elle n'en consomme.
2.3. Calculer, en MeV, l’énergie E1 libérée par cette réaction nucléaire.
Variation de masse |Dm| =m(23592 U) -m(9540 Zr)-m(13852 Te) - m(01n).
|Dm| =235,043 -(94,8860 +137,901 +1,00866)=1,24734 u.
soit 1,24734 x 1,06605 10-27 =1,32973 10-27 kg.
Valeur absolue de l'énergie libérée : |Dm| c2 = 1,32973 10-27 x (2,998 108)2 ~1,1952 10-10 J.
2.4. Calculer, en joules, l’énergie E2
libérée par la fission de 1,000 g d’uranium 235 puis par l’accident de
Tchernobyl en considérant que la masse d’uranium 235 présente dans le
réacteur était de 200 kg.
Masse d'un noyau d'uranium 235 : 235,043 x 1,6605 10-27 = 3,9029 10-25 kg = 3,9029 10-22 g.
E2 = 1,1952 10-10 / (3,9029 10-22) = 3,062 1011 J.
Energie libérée par l'accident : 3,062 1011 x200 103 =6,125 1016 J.
2.5.
En s’appuyant sur les données et les informations fournies, comparer
cette énergie à celle qui a été libérée lors de la catastrophe
d’Hiroshima. ( Explosion, équivalente à celle de 15 000 tonnes de
TNTsoit 15 000 x4,6 1012 =6,9 1016 J) .
Les énergies libérées lors d'Hiroshima et de Tchernobyl sont du même ordre de grandeur.
L’iode 131 est un des déchets radioactifs rejetés lors de l’accident nucléaire.
2.6. Ecrire l’équation de la désintégration ß- d’un noyau d’iode 131.
13153I ---> 13154Xe +0-1e
2.7. Au cours du temps, on a déterminé le nombre moyen N de noyaux d’iode 131. On note N0 le
nombre moyen de noyaux présents à l’état initial. Ecrire la loi de
décroissance radioactive en précisant la signification des différents
termes.
N = N0 exp(-lt).
l : constante radioactive en s-1; t : temps en s.
|
|
2.8. A l’aide du graphe et de la loi de décroissance radioactive, montrer que la constante radioactive de l’iode 131 vaut
l = 1,0 10-6 s-1. Expliquer la démarche suivie.
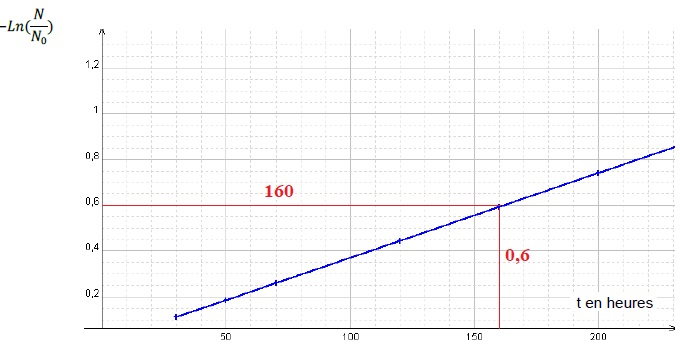
Le coefficient directeur de cette droite est égale à l.
0,60 /(3600 x160) =1,0 10-6 s-1.
2.9. Après avoir défini le temps de demi-vie t1/2 de l’iode 131, déterminer sa valeur.
Le temps de demi-vie est la durée au bout de laquelle l'activité initiale est divisée par deux.
l t½ = ln 2 ; t½ = ln 2 / (1,0 10-6 )=6,93 105 s ( ~192 heures )
Lors de l’accident de Tchernobyl, une grande quantité de noyaux radioactifs sont rejetés dans l’atmosphère ; parmi eux on trouve l’iode 131. Un nuage radioactif se forme. Il fera le tour de la Terre.
2.10. Lors de l’explosion, on estime que le nombre de noyaux émis est N = 4,1 1026 noyaux.
Calculer l’activité A0 lors de l’explosion.
A0 = l N = 1,0 10-6 x4,1 1026 = 4,1 1020 Bq.
2.11. Calculer l’activité A de l’iode dans l’atmosphère 30 ans plus tard.
2.12. Commenter cette valeur.
A = A0 exp(-lt) = 4,1 1020 exp(-1,0 10-6 x30 x365 x24 x3600) =5,4 10-391 ~0.
2.13. Les sols de Tchernobyl sont-ils, de nos jours, contaminés par l’iode 131. Justifier la réponse.
30 ans = 30 x365 x 24 =262 800 heures soit environ 262 800 / 192 ~1370 périodes rédioactives.
L'activité de l'iode 131 est quasiment nulle au bout de 30 ans. Les
sols, l'atmosphère ne sont plus contaminés par l'iode 131.
|
...
|
|
.
|
....
|
3. Impact du césium 137
Le césium 137 est également un émetteur ß- de demi-vie t1/2
= 30,1 ans. La contamination des sols à la suite de l’explosion est
principalement due à ce radionucléide. Selon le comité scientifique des
Nations Unies pour l’étude des effets des rayonnements atomiques
(UNSCEAR),
une surface d’aire S = 10 000 km2 de territoire de
l’Ex-Union Soviétique a été contaminée en 1986 avec du césium 137
produisant une radioactivité surfacique de 555 kBq.m-2. Ces territoires sont appelés zones de contrôle spécial.
3.1. Calculer le nombre de noyaux de césium 137 correspondant à une activité de 555 kBq.
l = ln 2 / t½ = ln 2 / ( 30,1 x365 x24 x3600 ) = 7,30 10-10 s-1.
N = A / l = 555 103 / ( 7,30 10-10 ) = 7,60 1014 noyaux.
3.2. Si on suppose
que la décroissance radioactive est la seule cause de décontamination
et qu’il n’y a pas de nouvel apport de césium 137, déterminer la date à
laquelle la radioactivité surfacique des territoires contaminés
atteindra 37 kBq.m-2, limite inférieure de
contamination selon l’UNSCEAR ?
A = A0 exp(-lt) ; -ln(A /A0 ) = l t.
l = ln (2) / 30,1 = 2,30 10-2 an-1.
-ln(A /A0 ) = - ln(37 / 555) = 2,708
t =2,708 / (2,30 10-2) ~118 ans.
Date : 1986 + 118 = 2104.
|
|
