Mathématiques,
BTS groupement B Nlle Calédonie 2019.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts. OK.
|
|
......
.....
|
Exercice 1. 10 points.
Dans cet exercice, on modélise le système de suspension d’une voiture radiocommandée par le schéma ci-dessous.
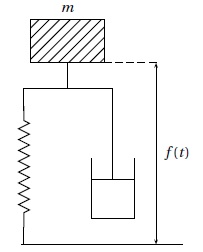
La masse m repose au sol à l’aide d’une suspension amortie.
On désigne par f (t ) la hauteur, en dm, par rapport au sol de la masse m à l’instant t en seconde.
On suppose que f est une fonction de la variable réelle t définie et deux fois dérivable sur [0 ; +∞[.
Les trois parties de cet exercice peuvent être traitées de façon indépendante.
A. Résolution d’une équatIon différentielle.
Une étude mécanique montre que la fonction f est solution de l’équation différentielle (E) :
y′′ +10y′ +25y = 20,
où y est une fonction inconnue de la variable réelle t , définie et deux fois dérivable sur [0 ; +∞[, y′ la
fonction dérivée de y et y′′ sa fonction dérivée seconde.
1. a. Résoudre dans R l’équation r 2 +10r +25 = 0.
Discriminant D =102-4 x25 = 0.
Solution r = (-10 +0) / 2 = -5.
b. En déduire les solutions, définies sur [0 ; +∞[ de l’équation différentielle (E0) :
y′′ +10y′ +25y = 0.
y = (At +B) e-5t avec A et B des constantes.
2. Cette question est une question à choix multiples. Une seule réponse est exacte.
La réponse juste rapporte un point. Une réponse fausse ou une absence de réponse ne rapporte ni n’enlève de point.
La fonction g définie sur [0 ; +∞[ par l’expression suivante est solution de l’équation différentielle (E) :
g (t ) = 0,8 ; g (t )= 20 ; g (t )= e−5t.
g(t) = 0,8 ; g'(t)= g"(t) = 0 ; repport dans (E) :
0 +0 +0,8 x25 =20.
3. En déduire les solutions de l’équation différentielle (E).
y = (At +B) e-5t +0,8
4. Les conditions initiales du système mécanique conduisent à poser f (0) = 0,4 el f ′(0) = 0.
Un logiciel de calcul formel fournit l’expression suivante de la fonction f .
y = −2t e−5t −0,4e−5t +0,8.
Quelle est la hauteur de la masse, en dm, au bout d’une seconde? Arrondir à 10−2.
y(1) = -2 e-5 -0,4 e-5 +0,8 ~0,78 dm.
B Étude de la fonction f
La fonction f est définie sur [0 ; +∞[ par
f (t ) = −2te−5t −0,4e−5t +0,8.
Sa courbe représentative C dans un repère orthogonal est donnée ci-dessous,
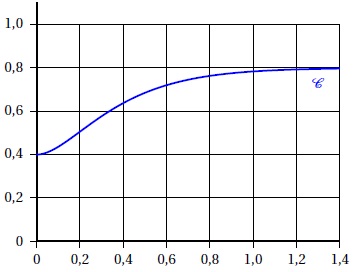
1. On admet le résultat suivant : la limite en plus l'infini de t e-5t est égale à zéro.
a. Calculer la limite de f(t) en plus l'infini.
En plus l'infini, e-5t tend vers zéro.
f(t) tend donc vers 0,8.
b. En déduire que la courbe C admet une droite asymptote dont on donnera une équation.
La droite d'équation y = 0,8 est asymptote à la courbe C.
2. a. Montrer que pour tout t de l’intervalle [0 ; +∞[, f ′(t )= 10te−5t .
f '(t) = 10t e-5t -2e-5t +2e-5t = 10te−5t .
b. Étudier le signe de f ′(t ) sur l’intervalle [0 ; +∞[,
Le terme en exponentielle est strictement positif.
f '(t) est positive. f(t) est croissante.
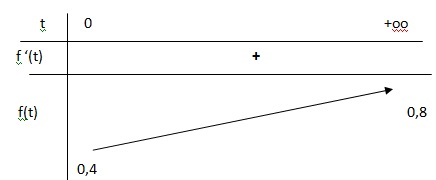
c. Dresser le tableau de variation de la fonction f sur l’intervalle [0 ; +∞[
3. Un logiciel de
calcul formel affiche la partie régulière du développement limité à
l’ordre 2 de la fonction f au voisinage de zéro.
0,4 + 5t2.
a. Donner une équation de la tangente T à la courbe C au point d’abscisse 0.
Coefficient directeur de cette tangente f ' (0) = 0.
La tangente passe au point de coordonnées (0 ; 0,4).
Equation de cette tangente : y= 0,4.
b. Étudier la position relative de la tangente T par rapport à la courbe C au voisinage de zéro.
f(t) -0,4 = −2t e−5t −0,4e−5t +0,8 -0,4 =−2t e−5t −0,4e−5t +0,4.
Au voisinage de zéro f(t)-0,4 = 0,4. La courbe est au dessus de la tangente à l'origine..
|
...
|
|
C. Dépassement d’un seuil et algorithmique.
On considère l’algorithme suivant.
t ←1,6
y ←(−2t −0,4)e−5t +0,8
Tant que 0,8− y > 10−3
t ←t +0,01
y ←(−2t −0,4)e−5t +0,8
Fin de Tant que.
1. Faire tourner cet algorithme « à la main» jusqu’a son arrêt, en complétant le tableau ci-dessous.
t
|
1,6
|
1,61
|
1,62
|
1,63
|
1,64
|
1,65
|
y ~
|
0,798 79
|
0,798 84
|
0,798 89
|
0,798 94
|
0,798 99
|
0,799 03
|
0,8 -y > 10-3
|
vrai
|
vrai
|
vrai
|
vrai
|
vrai
|
faux
|
2. Quelle est la valeur de la variable t a la fin de l’algorithme ? 1,65.
|
....
|
Exercice 2. 10 points.
Une
machine à commande numérique permet de fabriquer des panneaux en MDF
(panneaux de fibre de bois de moyenne densité) de 40 mm d’épaisseur.
Les trois parties de cet exercice peuvent être traitées de façon indépendante.
A. Loi normale.
Un panneau est considéré comme « acceptable » si son épaisseur est
comprise entre 39,78 mm et 40,22 mm. S’il n’est pas considéré comme
acceptable, il sera renvoyé au recyclage.
On note X la variable aléatoire qui, à chaque panneau fabriqué par la
machine, associe son épaisseur en mm. On admet que la variable
aléatoire X suit la loi normale de moyenne μ = 40 et d’écart type s inconnu.
1. En utilisant la capture d’écran ci-dessous, expliquer pourquoi on peut approcher la valeur de s par 0,1.
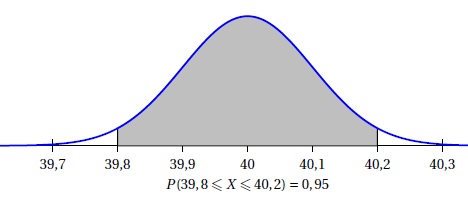
P(µ-2s < X < µ+2s) = 0,95.
µ+2s =40,2 ; 2s =40,2-40 = 0,2 ; s = 0,1.
2. On admet que s = 0,1.
a. Donner la probabilité, arrondie à 10−3, qu’un panneau, prélevé au hasard dans la production de la machine, soit considéré comme acceptable.
P(X < 39,78) =0,0139.
P(X < 40,22) =0,9861.
P (39,78 < X < 40,22 )= 0,9861-0,0139=0,972.
b) En déduire la probabilité, arrondie à 10−3, qu’un panneau, prélevé au hasard dans la production de la machine, soit envoyé au recyclage.
1-0,972 ~0,028.
B. Loi binomiale et loi de Poisson.
Un grossiste commande un lot de 200 panneaux en MDF.On admet que la
probabilité qu’un panneau prélevé au hasard dans la production soit
envoyé au recyclage est 0,03. La production est suffisamment importante
pour assimiler un lot de 200 panneaux comme résultant d’un tirage au
hasard avec remise dans la production.
On note Y la variable aléatoire qui, à tout lot de 200 panneaux ainsi
prélevé, associe le nombre de panneaux à envoyer au recyclage.
1. Justifier que la variable aléatoire Y suit une loi binomiale et préciser ses paramètres.
Les tirages sont indépendants les uns des autres. Il y a deux issues
possibles : panneau défectueu p = 0,03 = constante ; panneau bon 1-p =
0,97.
La variable aléatoire Y suit une loi binomiale de paramètres n = 200 et p = 0,03.
2. Calculer E(Y ) et interpréter le résultat.
E(Y) = np = 200 x0,03 = 6.
En moyenne, il y a 6 panneaux défectueux sur 200 panneaux.
3. Donner la probabilité, arrondie à 10−3, d’avoir dans un lot de 200 panneaux, au plus deux panneaux à envoyer au recyclage.
P(Y = 0) = 0,00226 ; P(Y = 1) = 0,013987 ; P(Y = 2) = 0,04304 ;
P(Y=0) +P(Y=1) +P(Y=2) = 0,0593~0,059.
4. On approche la loi de la variable aléatoire Y par une loi de Poisson de paramètre l. Soit Z une variable aléatoire qui suit cette loi de Poisson.
a. Justifier que l= 6.
l = np = 200 x0,03 = 6.
b. Donner la valeur arrondie à 10−3 de P(Z < 2).
P(Z < 2) = 0,06197 ~0,062.
c. Calculer l’écart entre les résultats des questions 3. et 4. b.
0,06197 -0,0593 ~0,0027 ~0,003.
|
C. Test d’hypothèse.
L’entreprise veut vérifier que la proportion de panneaux présentant un
défaut d’épaisseur est p = 0,03. Pour cela, elle réalise un test
d’hypothèse bilatéral au seuil de signification de 5% sur un
échantillon aléatoire de 400 panneaux prélevés dans le stock. Le stock
est suffisamment important pour assimiler ce prélèvement à un tirage
avec remise.
On note F la variable aléatoire qui, à tout échantillon aléatoire de
400 panneaux, associe la fréquence des panneaux présentant un défaut
d’épaisseur. On suppose que F suit la loi normale de moyenne p inconnue
et d’écart type [ p(1−p) /400]½.
L’hypothèse nulle H0 est : « p = 0,03 ».
L’hypothèse alternative H1 est :« p diffère de 0,03 ».
1. Justifier que sous l’hypothèse H0 l’écart type de la variable aléatoire F est environ 0,009.
[ p(1−p) /400]½ =(0,03 x0,97/ 400)½~0,00853 ~0,009.
2.
Cette question est une question à choix multiples. Une seule réponse
est exacte. La réponse exacte rapporte un point. Une réponse
fausse ou une absence de réponse ne rapporte ni n’enlève de point.
Soit a le réel positif, tel que, sous l’hypothèse H0, P(0,03−a < F < 0,03+a) = 0,95.
Une valeur approchée de a à 10−3 près est :
0,009 ; 0,017 ; 0,023.
a = 1,96 s / n½ =1,96 x 0,009 / 400½ =0,00088 ~0,0009.
Intervalle [0,03 -0,0009 ; 0,03 +0,0009] soit [ 0,0291 ;0,0309 ].
3. Énoncer la règle de décision du test.
Si F appartient à l'intervalle [ 0,0291 ;0,0309 ], on accepte H0 au seuil de 5 %.
Dans le cas contraire, on accepte H1 au risque de 5 %.
4. Sur l’échantillon aléatoire de 400 panneaux prélevés, on a relevé 18 panneaux ayant un défaut d’épaisseur.
Quelle est la conclusion du test ?
Fréquence des panneaux ayant un défaut : 18 / 400 =0,045.
Cette valeur n'appartient pas à l'intervalle [ 0,0291 ;0,0309 ]. L'hypothèse H0 est rejetée. On retient l'hypothèse H1.
|
|
|



