Mathématiques, Brevet Amérique du Nord 2019

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

Exercice 1 . ( 14 points )
On considère la figure ci-dessous, réalisée à main levée et qui n’est pas à l’échelle.
On donne les informations suivantes :
les droites (ER) et (FT) sont sécantes en A ;
AE= 8 cm, AF= 10 cm, EF = 6 cm ; AR = 12 cm, AT= 14 cm

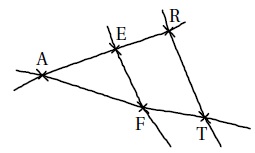
1. Démontrer que le triangle AEF est rectangle en E.
AF² = 10² = 100 ; AE² +EF² =8² +6² =64 +36 = 100.
AF² =AE² +EF² .
D'après la réciproque du théorème de Pythagore, e triangle AEF est rectangle en E.
2. En déduire une mesure de l’angle EAF au degré près.
Dans le triangle rectangle AEF, sin EAF = EF / AF = 6 / 10 = 0,60; l'angle EAF mesure environ 37 °.
3. Les droites (EF) et (RT) sont-elles parallèles ?
AR / AE = 12 / 8 = 1,5 ; AT / AF = 14 / 10 = 1,4.
AR / AE diffère de AT / AF ; les droites (EF) et (RT) ne sont pas parallèles.

Exercice 2 ( 17 points).
Voici quatre affirmations. Pour chacune d’entre elles, dire si elle est vraie ou fausse. On rappelle que la réponse doit être justifiée.
1. Affirmation 1 :

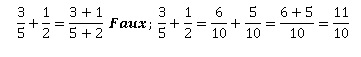
2. On considère la fonction f : f(x) = 5 -3x.
Affirmatíon 2 : l’image de −1 par f est −2. Faux.
f(-1) = 5-3 (-1)= 8.
3. On considère deux expériences aléatoires :
- expérience n° 1 : choisir au hasard un nombre entier compris entre 1 et 11 (1 et 11 inclus).
- expérience n° 2 : lancer un dé équilibré à six faces numérotées de 1 à 6 et annoncer le nombre qui apparait sur la face du dessus.
Affirmation 3 : il est plus probable de choisir un nombre premier dans l’expérience n° 1 que d’obtenir un nombre pair dans l’experience n° 2. Faux.
Expérience n°1 : 2, 3, 5, 7, 11 sont premiers soit 5 cas favorables sur 11 possibilités ; la probabilité est : 5 / 11~0,45.
Expérience n°2 : 2, 4, 6 soit 3 cas favorables sur 6 possibilités ; la probabilité est 3 / 6 = 0,5.
4. Affirmation 4 : pour tout nombre x, (2x +1)² −4 = (2x +3)(2x −1).Vrai.
(2x +1)² −2² =[2x+1+2] [2x+1-2] =(2x+3)(2x-1).

Exercice 3 (12 points).
Le diagramme ci-dessous représente, pour six pays, la quantité de nourriture gaspillée (en kg) par habitant en 2010.

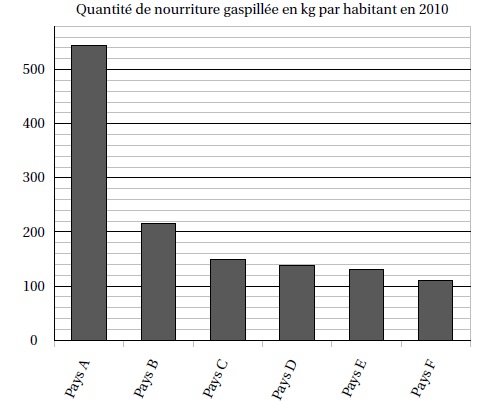
1. Donner approximativement la quantité de nourriture gaspillée par un habitant du pays D en 2010.
140 kg.
2. Peut-on affirmer que le gaspillage de nourriture d’un habitant du pays F représente environ un cinquième du gaspillage de nourriture d’un habitant du pays A?
Pays F : 105 kg ; pays A : 540 kg. 540 / 5 =108 kg, voisin de 105 kg, donc affirmation vraie.
3. On veut rendre compte de la quantité de nourriture gaspillée pour d’autres pays. On réalise alors le tableau ci-dessous à l’aide d’un tableur. Rappel : 1 tonne = 1 000kg.

	A	B	C	D
1		Quantité de nourriture gaspillée par habitant en 2010 ( kg)	Nombre d'habitants en 2010 ( millions)	Quantité totale de nourriture gaspillée (tonnes)
2	pays X	345	10,9	3 760 500
3	pays Y	212	9,4
4	pays Z	135	46,6

a. Quelle est la quantité totale de nourriture gaspillée par les habitants du pays X en 2010 ?
3 760 500 tonnes.
b. Voici trois propositions de formule, recopier sur votre copie celle qu’on a saisie dans la cellule D2 avant de l’étirer jusqu’en D4.
= B2*C2*1 000 000 ; =B2*C2 ; =B2*C2*1000.

Exercice 4. ( 10 points).
On a programmé un jeu. Le but du jeu est de sortir du labyrinthe. Au début du jeu, le lutin se place au point de départ. Lorsque le lutin
touche un mur, représenté par un trait noir épais, il revient au point de départ.

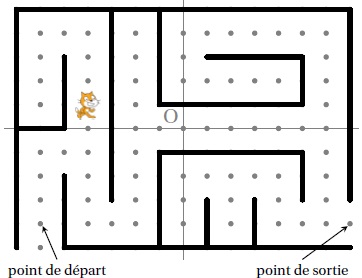
L’arrière-plan est constitué d’un repère d’origine O avec des points espacés de 30 unités verticalement et horizontalement.
Dans cet exercice, on considèrera que seuls les murs du labyrinthe sont noirs.
Voici le programme :

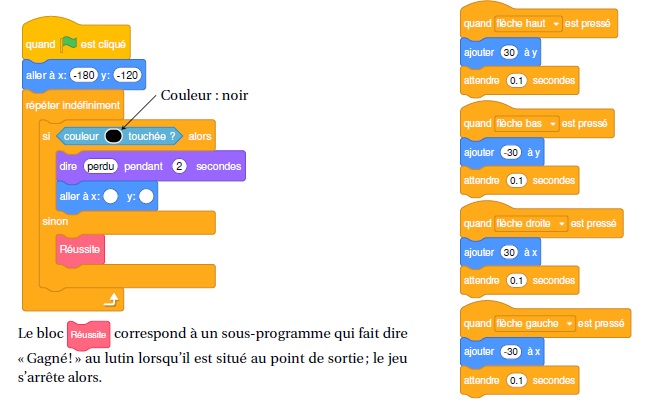
1. Recopier et compléter l’instruction aller à x: y: du programme pour ramener le lutin au point de départ si la couleur noire est touchée.
aller à x = -180 ; y = -120.
2. Quelle est la distance minimale parcourue par le lutin entre le point de départ et le point de sortie ?
27 x 30 = 810 unités.
3. On lance le programme en cliquant sur le drapeau. Le lutin est au point de départ. On appuie brièvement sur la touche ↑ (« flèche haut ») puis sur la touche→(« flèche droite »). Quelles sont toutes les actions effectuées par le lutin ?
y = -120 +30 = -90 ;x = 180 +30 = -150 ; mur touché, perdu, retour à la case départ.

Exercice 5. ( 10 points).
Dans cet exercice, aucune justification n’est attendue
On considère l’hexagone ABCDEF de centre O représenté ci-dessous.

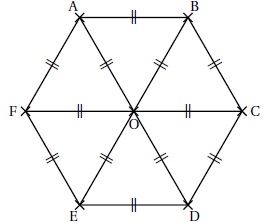
1. Parmi les propositions suivantes, recopier celle qui correspond à l’image du quadrilatère CDEO par la symétrie de centre O.
Proposition 1 : FABO ; Proposition 2 : ABCO ; Proposition 3 : FODE
2. Quelle est l’image du segment [AO] par la symétrie d’axe (CF) ?
Segment [EO]
3. On considère la rotation de centre O qui transforme le triangle OAB en le triangle OCD.
Quelle est l’image du triangle BOC par cette rotation ?
Triangle EOD.
La figure ci-dessous représente un pavage dont le motif de base a la même forme que l’hexagone ci-dessus. On a numéroté certains de ces hexagones.
4. Quelle est l’image de l’hexagone 14 par la translation qui transforme l’hexagone 2 en l’hexagone 12 ?

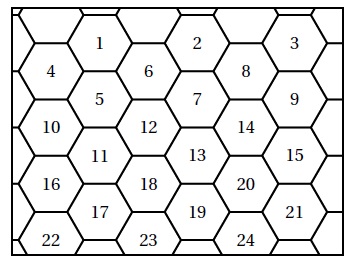
Hexagone 19.

.............

Exercice 6. 12 points.
Les deux parties A et B sont indépendantes.
Partie A : absorption du principe actif d’unmédicament
Lorsqu’on absorbe un médicament, que ce soit par voie orale ou non, la quantité de principe actif de ce médicament dans le sang évolue en fonction du temps. Cette quantité semesure en milligrammes par litre de sang.
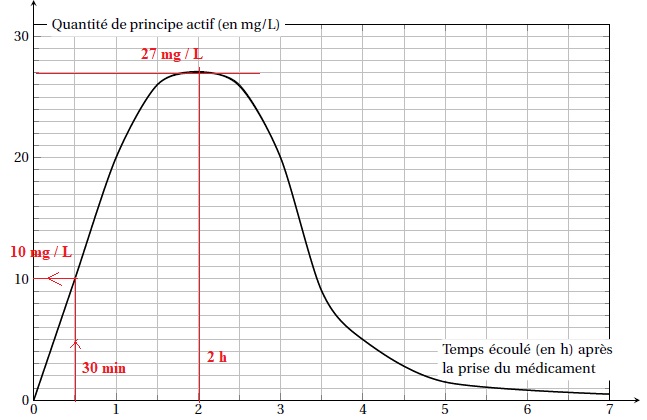
Le graphique ci-dessous représente la quantité de principe actif d’un médicament dans le sang, en fonction du temps écoulé, depuis la prise de ce médicament.
1. Quelle est la quantité de principe actif dans le sang, trente minutes après la prise de ce médicament ?
2. Combien de temps après la prise de ce médicament, la quantité de principe actif est-elle la plus élevée?

Partie B : comparaison de masses d’alcool dans deux boissons
On fournit les données suivantes :
Formule permettant de calculer la masse d’alcool en g dans une boisson alcoolisée : m =V ×d ×7,9
V : volume de la boisson alcoolisée en cL ; d : degré d’alcool de la boisson
(exemple, un degré d’alcool de 2% signifie que d est égal à 0,02)
Deux exemples de boissons alcoolisées :
Boisson 1 : Degré d’alcool : 5% ; Contenance : 33 cL.
Boisson 2 :Degré d’alcool : 12% ; Contenance 125 mL.
La boisson 1 contient-elle une masse d’alcool supérieure à celle de la boisson 2 ?
m₁ = 33 x0,05 x7,9 ~13,0 g.
m₂ = 12,5 x0,12 x7,9 ~11,80 g.
La boisson 1 contient une masse d’alcool supérieure à celle de la boisson 2.

Exercice 7. 15 points.
Pour ranger les boulets de canon, les soldats du XVI^e siècle utilisaient souvent un type d’empilement pyramidal à base carrée, comme le montrent les dessins suivants :

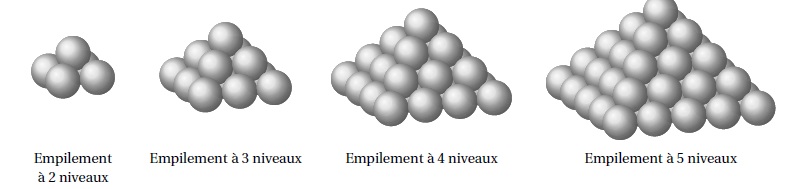
1. Combien de boulets contient l’empilement à 2 niveaux ?
4 +1 = 5.
2. Expliquer pourquoi l’empilement à 3 niveaux contient 14 boulets.
Niveau 1 : 3 x3 = 9 ; niveau 2 : 2 x 2 = 4 ; niveau 3 : 1 ; total : 9 +4 +1 = 14.
3. On range 55 boulets de canon selon cette méthode. Combien de niveaux comporte alors l’empilement obtenu ?
Niveau 1 : 5 x5 = 25 ; niveau 2 : 4 x 4 = 16 ; niveau 3 : 3 x3 = 9 ; niveau 4 : 2 x2 = 4 ; niveau 5 : 1 ; total : 25 +16 +9 +4 +1 = 55.
4. Ces boulets sont en fonte ; la masse volumique de cette fonte est de 7 300 kg / m³.
On modélise un boulet de canon par une boule de rayon 6 cm.
Montrer que l’empilement à 3 niveaux de ces boulets pèse 92 kg, au kg près.
Volume d’un boulet =4 /3 x 3,14 x6³ =904,77 cm³.
7 300 kg / m³= 7,3 g / cm³ ;
Masse d'un boulet : 904,77 x7,3 =6605 g = 6,6 kg.
Masse d 14 boulets ; 6,6 x14 ~92 kg.

Exercice 8. ( 10 points )
Dans une classe de Terminale, huit élèves passent un concours d’entrée dans une école d’enseignement supérieur.
Pour être admis, il faut obtenir une note supérieure ou égale à 10.
Une note est attribuée avec une précision d’un demi-point (par exemple : 10 ; 10,5; 11; . . .) On dispose des informations suivantes :
Information 1 :
Notes attribuées aux 8 élèves de la classe qui ont passé le concours : 10; 13; 15; 14,5; 6; 7,5 ; X ; Y.
Information 2 :
La série constituée des huit notes :
- a pour étendue 9;
- a pour moyenne 11,5;
- a pour médiane 12.
75% des élèves de la classe qui ont passé le concours ont été reçus.
1. Expliquer pourquoi il est impossible que l’une des deux notes manquantes soit 16.
6 ; 7,5 ; 10 ; 13 ; 14,5 ; 15 ;16 ; l'étendue serait égale à 16-6 = 10. Donc ce n'est pas possible.
2. Est-il possible que les deux notes manquantes soient 12,5 et 13,5 ?
6 ; 7,5 ; 10 ; 12,5 ; 13 ; 13,5 ; 14,5 ; 15.
La médiane est comprise entre 12,5 et 13. Donc ce n'est pas possible.
La moyenne est égale à :11,5.
L'étendue est égale à 15 -6 = 9.