Mathématiques, Brevet Polynésie septembre 2019

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

Exercice 1 . ( 15 points )
Dans ce questionnaire à choix multiples, pour chaque question des réponses sont proposées, une seule est exacte. Sur la copie, écrire le numéro de la question et recopier la bonne réponse. Aucune justification n’est attendue.
1. Le nombre (-2)⁴ est égal à : 16 ; - 8 ; 20 000.
2. Une vitesse de 90 km / h est égale à : 0,025 m/s ; 25 000 m /s ; 25 m /s.
90 / 3,6 = 25 m /s.
3. La décomposition en produit de facteurs premiers de 24 est :
2 x3 x4 ; 2 x2 x2 x3 ; 2 x2 x6.
4. Soit f la fonction affine définie par f : x → 2x + 5
L’image de – 1 par la fonction f est : 3 ; 6 ; - 7.
2 *(-1) +5 = 3.
5. Si on multiplie par 3 toutes les dimensions d’un rectangle, son aire est multipliée par : 3 ; 6 ; 9.

Exercice 2 ( 12 points).
Hugo a téléchargé des titres musicaux sur son téléphone. Il les a classés par genre musical comme indiqué dans le tableau ci-dessous :

Genre musical	Pop	Rap	Techno	Variété française
Nombre de titre	35	23	14	28

1) Combien de titres a-t-il téléchargés ?
35+23+14+28=100.
2) Il souhaite utiliser la fonction « lecture aléatoire » de son téléphone qui consiste à choisir au hasard parmi tous les titres musicaux téléchargés, un titre à diffuser. Tous les titres sont différents et chaque titre a autant de chances d’être choisi. On s’intéresse au genre musical du premier titre diffusé.
a) Quelle est la probabilité de l’événement : « Obtenir un titre Pop » ?
35 / 100 = 0,35.
b) Quelle est la probabilité de l’événement « Le titre diffusé n’est pas du Rap » ?
(100 -23) / 100 = 0,77.
c) Un fichier musical audio a une taille d’environ 4 Mo (Mégaoctets). Sur le téléphone d’Hugo, il reste 1,5 Go (Gigaoctet) disponible. Il souhaite télécharger de nouveaux titres musicaux. Combien peut-il en télécharger au maximum ?
Rappel : 1 Go = 1 000 Mo.
1500 /4 =375.

Exercice 3 (14 points).
Une assistante maternelle gardait plusieurs enfants dont Farida qui est entrée à l’école en septembre 2017. Ses parents ont alors rompu leur contrat avec cette assistante maternelle. La loi les oblige à verser une « indemnité de rupture ».
Le montant de cette indemnité est égal au 1/120ème du total des salaires nets perçus par l’assistante maternelle pendant toute la durée du contrat.
Ils ont reporté le montant des salaires nets versés, de mars 2015 à août 2017, dans un tableur comme ci-dessous :

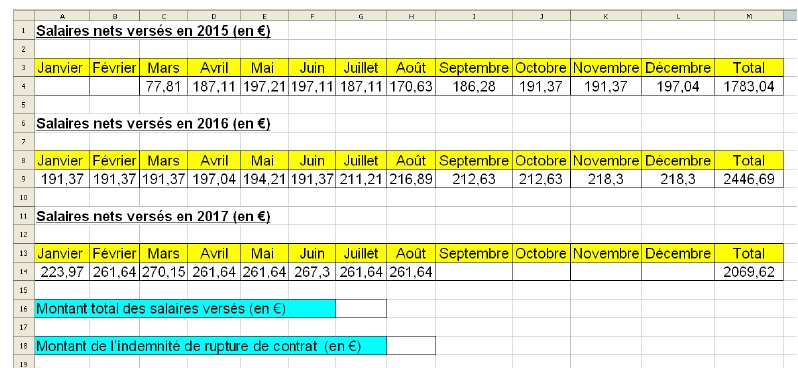
1) a) Que représente la valeur 1783,04 dans la cellule M4 ?
Le montant total ses salaires versés en 2015.
b) Quelle formule a-t-on écrit dans la cellule M4 pour obtenir cette valeur ?
=Somme(C4;L4)
c) Dans quelle cellule doit-on écrire la formule = M4 + M9 + M14 ?
G16.
2) Déterminer le montant de « l’indemnité de rupture ». Arrondir au centime d’euro près.
1 /20ème = 0,05 ; (1783,04 +2446,69 +2069,62) x0,05=314,97 €.
3) Déterminer le salaire moyen net mensuel versé à cette assistante maternelle sur toute la durée du contrat de la famille de Farida. Arrondir au centime d’euro près.
(1783,04 +2446,69 +2069,62) / 30 =209,98 €.
4) Calculer l’étendue des salaires versés.
270,15-77,81=192,34 €.

Exercice 4. ( 16 points).
On s’intéresse aux ailes d’un moulin à vent décoratif de jardin. Elles sont représentées.
On donne :
· BCDE, FGHI, JKLM et PQRS sont des rectangles superposables.
· C, B, A, J, K d’une part et G, F, A, P, Q d’autre part sont alignés.
· AB = AF = AJ = AP.

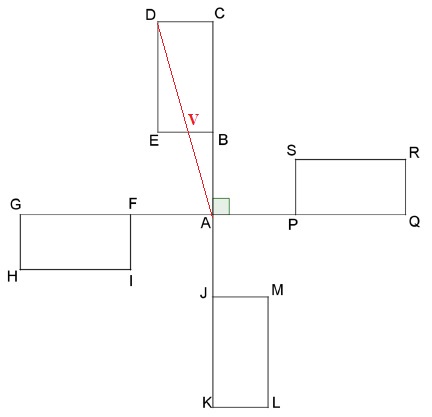
1) Quelle transformation permet de passer du rectangle FGHI au rectangle PQRS ?
Rotation de centre A et d'angle 180° dans le sens inverse des aiguilles d'une montre.
2) Quelle est l’image du rectangle FGHI par la rotation de centre A d’angle 90° dans le sens inverse des aiguilles d’une montre ?
Rectangle JKLM.
3) Soit V un point de [EB] tel que BV = 4 cm.
On donne : AB = 10 cm et AC = 30 cm.
a) Justifier que (DC) et (VB) sont parallèles.
Le quadrilatère BCDE est un rectangle. Les droites (DC) et (EB) sont parallèles.
b) Calculer DC.
Thalès : DC / VB = AC / AB ; DC / 4 = 30 / 10 = 3 ; DC = 12 cm.
c) Déterminer la mesure de l’angle DAC. Arrondir au degré près.
tan(DAC) = DC / AC = 12 / 30 = 0,4 ; l'angle DAC mesure environ 22°.

Exercice 5. ( 16 points).
On a construit un bac à sable pour enfants. Ce bac a la forme d’un prisme droit de hauteur 15 cm. La base de ce prisme droit est représentée
par le polygone ABCDE ci-dessous :
On donne :
· PC = PD = 1,30 m
· ED = BC = 40 cm
· E, D, P sont alignés
· B, C, P sont alignés

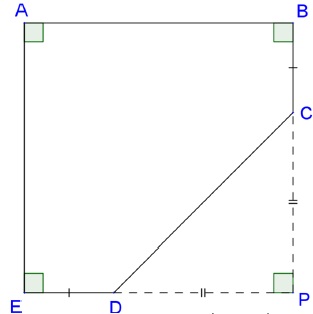
1)Calculer CD. Arrondir au centimètre près.
Le triangle CDp est isocèle et rectangle en P.
CD = CP x racine carrée (2) ~1,30 x1,414 ~ 1,84 m.
2) Justifier que le quadrilatère ABPE est un carré.
Les quatre angles sont droits ; de plus EP = 1,30 +0,40 = 1,70 m. BP = 1,30 +0,40 = 1,70 m.
3) En déduire le périmètre du polygone ABCDE. Arrondir au centimètre près.
1,70 +1,70 +0,40 +1,84 +0,40 =6,04 m.
4) On a construit le tour du bac à sable avec des planches en bois de longueur 2,40 m et de hauteur 15 cm chacune. De combien de planches a-t-on eu besoin ?
AB + BC = 2,10 m soit une planche.
AE + ED = 2,10 m soit une planche.
CD = 1,84 m soit une planche.
Total : 3 planches.
5) Calculer, en m², l’aire du polygone ABCDE.
Aire du carré ABPE : 1,70 x1,70 = 2,89 m².
Aire du triangle CDP : 1,3 x1,3 / 2 =0,845 m².
Aire du quadrilatère ABCDE : 2,89 -0,845=2,045 m².
6) A-t-on eu besoin de plus de 300 L de sable pour remplir complètement le bac ?
Volume du bac = aire de base x hauteur =2,045 x0,15 ~0,307 m³ soit 307 L.
Il faut plus de 300 L de sable.

Exercice 6. 15 points.
L’éco-conduite est un comportement de conduite plus responsable permettant de :
· réduire ses dépenses : moins de consommation de carburant et un coût d’entretien du véhicule réduit ; · limiter les émissions de gaz à effet de serre ;
· réduire le risque d’accident de 10 à 15 % en moyenne.
1) Un des grands principes est de vérifier la pression des pneus de son véhicule. On considère des pneus dont la pression recommandée par le constructeur est de 2,4 bars.
a) Sachant qu’un pneu perd environ 0,1 bar par mois, en combien de mois la pression des pneus sera descendue à 1,9 bar, s’il n’y a eu aucun gonflage ?
(2,4 -1,9) /0,1 = 5 mois.
b) Le graphique ci-dessous donne un pourcentage approximatif de consommation supplémentaire de carburant en fonction de la pression des pneus (zone grisée) :

D’après le graphique, pour des pneus gonflés à 1,9 bars alors que la pression recommandée est de 2,4 bars, donner un encadrement approximatif du pourcentage de la consommation supplémentaire de carburant.
[2 ; 4,2 ]
2) Paul a remarqué que lorsque les pneus étaient correctement gonflés, sa voiture consommait en moyenne 6 L aux 100 km. Il décide de s’inscrire à un stage d’éco-conduite afin de diminuer sa consommation de carburant et donc l’émission de CO₂. En adoptant les principes de l’écoconduite,
un conducteur peut diminuer sa consommation de carburant d’environ 15 %. Il souhaite, à l’issue du stage, atteindre cet objectif.
a) Quelle sera alors la consommation moyenne de la voiture de Paul ?
6 x0,85 =5,1 L.
b) Sachant qu’il effectue environ 20 000 km en une année, combien de litres de carburant peut-il espérer économiser ?
0,9 x 200 =180 L.
c) Sa voiture roule à l’essence sans plomb. Le prix moyen est 1,35 €/L. Quel serait alors le montant de l’économie réalisée sur une année ?
180 x1,35 ~243 €.
d) Ce stage lui a coûté 200 €. Au bout d’un an peut-il espérer amortir cette dépense ? Oui.

Exercice 7. 14 points.
On donne le programme ci-dessous où on considère 2 lutins. Pour chaque lutin, on a écrit un script correspondant à un programme de calcul différent.

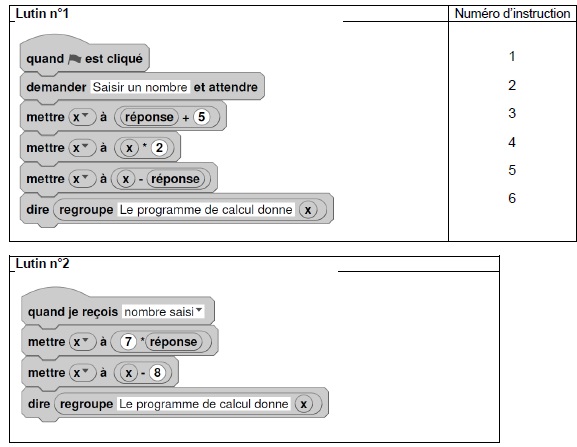
1) Vérifier que si on saisit 7 comme nombre, le lutin n°1 affiche comme résultat 17 et le lutin n°2 affiche 41.
Lutin n°1 : 7+5 = 12 ; 12 x 2 =24 ; 24 -7 =17.
Lutin n°2 : 7 x 7 =49 ; 49-8 =41.
2) Quel résultat affiche le lutin n° 2 si on saisit le nombre - 4 ?
-4 x7 = -28 ; -28-8= -36.
3) a) Si on appelle x le nombre saisi, écrire en fonction de x les expressions qui traduisent
le programme de calcul du lutin n°1, à chaque étape (instructions 3 à 5).
b) Montrer que cette expression peut s’écrire x+ 10.
x+5 ; (x+5) * 2 = 2x +10 ; 2x+10 -x = x+10.
4) Célia affirme que plusieurs instructions dans le script du lutin n°1 peuvent être supprimées et remplacées par celle ci-dessous :
"Mettre x à réponse +10".
Indiquer, sur la copie, les numéros des instructions qui sont alors inutiles.
Les instructions 3 à 5 sont inutiles.
5) Paul a saisi un nombre pour lequel les lutins n°1 et n°2 affichent le même résultat. Quel est ce nombre ?
Lutin n°1 : x+10.
Lutin n°2 : 7x-8.
x+10 = 7x-8 ; 10+8 = 7x-x ; 18 = 6x : x = 3.