Mathématiques, Brevet Polynésie 2019

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

Exercice 1 . QCM ( 12 points )
1. La décomposition en produit de facteurs premiers de 24 est : 2 x3 x4 ; 2 x2 x2 x2 x3 ; 2 x2 x6.
2. Lequel de ces nombres est premier ?
2265 est divisible par 5.
8191 : ces seuls diviseurs sont 1 et 8191.
7113 est divisible par 3.
3. La roue B fait 2 tours. Combien de tours fait la roue A ?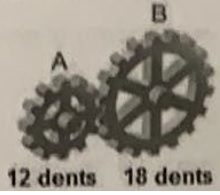

3 tours ; 4 tours ; 5 tours.
18 x2 / 12 =3 tours.
4. Une justification est attendue.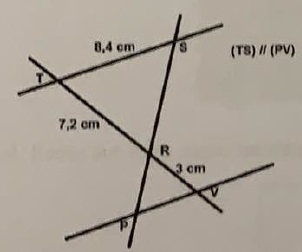

PV = 3 cm ; PV = 20,16 cm ; PV = 3,5 cm.
(TS) parallèle à (PV).
Les points TR et V sont alignés. Les points SR et P sont alignés.
Thalès : TR / RV = TS / PV ; PV = TS x RV / TR = 8,4 x 3 / 7,2 =3,5 cm.

Exercice 2 ( 20 points).
1. On a utilisé une feuille de calcul pour obtenir les images de différentes valeurs de x par une fonction affine f.
B2=3*B1-4

	A	B	C	D	E	F	G	H
1	x	-2	-1	0	1	2	3	4
2	f(x)	-10	-7	-4	-1	2	5	8

a. Quelle est l'image de -1 par la fonction f ?
f(-1) =-7.
b. Quel est l'antécédent de 5 par la fonction f ?
f(3) = 5.
c. Donner l'expression de f(x).
f(x) = 3x-4.
d. Calculer f(10).
f(10) = 3 x10-4 = 26.
2. On donne le programme suivant qui traduit un programme de calcul..

a. Ecrire sur votre copie les deux dernières étapes du programme de calcul.
Choisir un nombre.
Ajouter 3 à ce nombre.
Multiplier le résultat par 2.
Retrancher 5 au résultat.
b. Si on choisit 8 au départ, quel sera le résultat ?
8+3 = 11 ; 11 x2 = 22 ; 22-5 = 17.
c. Si on choisit x au départ, montrer que le résultat est 2x+1.
x+3 ; 2(x+3) ; 2(x+3)-5=2x+6-5 =2x+1.
d. Quel nombre doit-on choisir au départ pour obtenir 6 ?
6 = 2x+1 ; 6-1 = 2x ; 5 = 2x ; x = 2,5.
3. Quel nombre faudrait-il choisir pour que la fonction f et le programme de calcul donne le même résultat ?
2x+1 = 3x-4 ; 1+4 = 3x-2x ; x = 5.

Exercice 3 (15 points).
Sam préfère les bonbons bleus.
Dans un paquet de 500 bonbons, 150 sont bleus, les autres sont rouges, jaunes ou verts.
1. Quelle est la probabilité qu'il pioche un bonbon bleu dans son paquet ?
150 / 500 = 15 / 50 =0,3.
2. 20 % des bonbons sont rouges. Combien y a t-il de bonbons rouges ?
500 x0,20 = 100.
3. Sachant qu'il y a 130 bonbons verts dans le paquet, Sam a t-il plus de chance de piocher au hasard un bonbon vert ou un bonbon jaune ?.
Probabilité de piocher un bonbon vert : 130 /500 = 0,26.
Nombre de bonbons jaunes : 500 -150 -130 -100=120.
Probabilité de piocher un bonbon jaune : 120 /500 = 0,24.
Il a plus de chance de tirer un bonbon vert qu'un bonbon jaune.
4. Aïcha a acheté le même paquet il y a quinze jours. Il ne lui reste que 140 bonbons bleus, 100 jaunes, 60 rouges et 100 verts. Elle dit à Sam " tu devrais piocher dans mon paquet, plutôt que dans le tien, tu aurais plus de chance d'obtenir un bleu". A-t-elle raison ?
Probabilité de piocher un bonbon bleu dans le paquet d'Aïcha :140 / (140 +100 +60 +100) =140 / 400= 0,35
Probabilité de piocher un bonbon bleu dans le paquet de Sam :150 / 500 = 0,3.
Aicha a raison.

Exercice 4. ( 12 points).
La pyramide du Louvre est une pyramide à base carrée de côté 35,4 m et de hauteur 21,6 m. C'est une réduction de la pyramide de Khéops, qui mesure 230,5 m de côté.
1. Montrer que la hauteur de la pyramide de Kéops est d'environ 140,6 m.
Facteur de réduction : 35,4 / 230,5 ~0,1536.
Hauteur de la pyramide de Khéops : 21,6 / 0,1536 ~140,6 m.
2. Calculer le volume de la pyramide du Louvre.
Aire de base x hauteur / 3 = 35,4 x35,4 x21,6 / 3 ~9023 m³.
3. Par quel nombre peut-on multiplier le volume de la pyramide du Louvre pour obtenir celui de la pyramide de Khéops ?
Chaque dimension doit être multipliée par 1 /0,1536 ~6,51.
Il faut multiplier le volume de la pyramide du Louvre par 6,51³ ~276.

Exercice 5. ( 14 points).
Lorsqu'un voilier est face au vent, il ne peut pas avancer.
Comparer les trajectoires de ces deux voiliers en calculant la distance en km et arrondie au dixième, que chacun a parcourue.

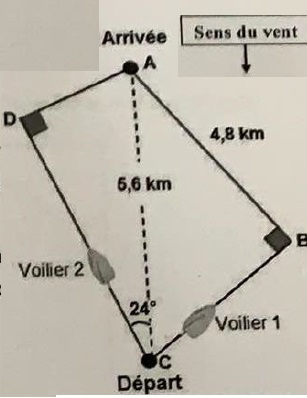
Voilier 1 : BC² = AC² -AB² = 5,6² -4,8² =8,32 ; BC ~2,9 km.
AB + BC =4,8 +2,9 =7,7 km.
Voilier 2 : CD = 5,6 cos 24 ~5,1 km.
AD = 5,6 sin 24 ~2,3 km.
CD + AD = 5,1 +2,3 =7,4 km.

Exercice 6. 12 points.
Voici un tableau regroupant les résultats de la finale du 200 m hommes remportée par Usain BOLT en 19,78 s ( en 2016).

Rang	Athlète	Nation	Performance (s)
1	U.BOLT	Jamaïque	19,78
2	A. De Grasse	Canada	20,02
3	C.Lemaitre	France	20,12
4	A.Gemili	Grande Bretagne	20,12
5	C. Martina	Hollande	20,13
6	L. Merrit	USA	20,19
7	A. Edward	Panama	20,23
8	R Guliyev	Tutquie	20,43

1. Calculer la vitesse moyenne de l'athlète le plus rapide.
200 / 19,78 ~10,11 m /s.
2. Calculer la moyenne des performance des athlètes.
(19,78 +20,02 +20,12 +20,12 +20,13 +20,19 +20,23 +20,43) / 8 ~20,13 s.
3. En 1964 à Tokyo, la moyenne des performances des athlètes sur 200 m hommes était de 20,68 s et l'étendue était de 0,6. En comparant ces résultats à ceux de 2016, qu'observe t-on ?
En 2016, les athlètes ont été plus rapides.
Etendue de la série en 2016 : 20,43 -19,78 =0,65.
Les étendues sont à peu près identiques.

Exercice 7. 15 points.
Le graphique ci-dessous donne les hauteurs d'eau au port de la Rochelle le 15/08/2018.

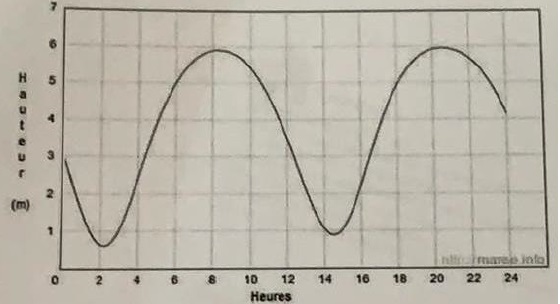
1. Quel a été le plus haut niveau ?

2. A quelles heures approximativement la hauteur d'eau a-t-elle été de 5 m ?
6 h ; 10h 20 ; 18 h ; 22 h35.
3.a Calculer le temps qui s'est écoulé entre la marée haute et la marée basse.
14 h30 -8 h16 = 6 h 14.
3.b. Calculer la différence de hauteur d'eau entre la marée haute et la marée basse.
5,89 -0,90 =4,99 m.

	Heure	Hauteur (m)
Marée haute	8 h 16	5,89
Marée basse	14 h30	0,90

4. Comment qualifier la marée du 15 août 2018 entre 8 h16et 14 h30 à La Rochelle ?
Coefficient de marée = (H_haut-H_bas) /5,34 x100 =4,99 / 5,34 x100 ~ 93.
Cette valeur étant supérieure à 70, la marée est qualifiée de vives-eaux.