Mathématiques, Brevet Métropole 2019

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

Exercice 1 . ( 10 points )
Le capitaine d'un navire possède un trésor constitué de 69 diamants, 1 150 perles et 4 140 pièces d'or.
1. Décomposer 69 ; 1 150 et 4 140 en produits de facteurs premiers.
69 = 3 x 23 ; 1150 = 2 x 5² x 23 ; 4140 = 2² x 3² x 5 x 23.
2. Le capitaine partage équitablement le trésor entre les marins.
Combien y-a-t-il de marins sachant que toutes les pièces, perles et diamants ont été distribués ?
PGCD(69 ;1150 ; 4140) = 23. Il y a 23 marins.

Exercice 2 ( 19 points).
Dans cet exercice, on donnera, si nécessaire, une valeur approchée des résultats au centième près.
Pour construire le décor d’une pièce de théâtre (Figure 1), Joanna dispose d’une plaque rectangulaire ABCD de 4 m sur 2 m dans laquelle elle doit découper les trois triangles du décor avant de les superposer. Elle propose un découpage de la plaque (Figure 2).

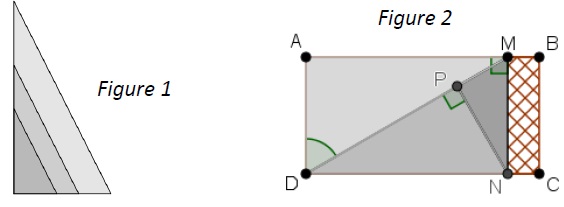
Le triangle ADM respecte les conditions suivantes :
 Le triangle ADM est rectangle en A
 AD = 2 m
 L'angle ÂDM mesure 60°.
1. Montrer que [AM] mesure environ 3,46 m.
Dans le triangle AMD, rectangle en A : tan 60 = AM / AD ; AM = AD tan 60 = 2 x1,732 ~3,46 m.
2. La partie de la plaque non utilisée est représentée en quadrillé sur la figure 2. Calculer une valeur approchée au centième de la proportion de la plaque qui n’est pas utilisée.
AM x AD = 3,46 x2 = 6,92 m² ; aire de la plaque : 4 x 2 = 8 m².
Aire de la partie non utilisée : 8-6,92 = 1,08 m² soit 1,08 / 8 x100 =13,5 % ~14 %.
3. Pour que la superposition des triangles soit harmonieuse, Joanna veut que les trois triangles AMD, PNM et PDN soient semblables. Démontrer que c’est bien le cas.
Les trois triangles sont rectangles.
Dans le triangle rectangle PDN, l'angle DNP mesure 60.
Dans le triangle rectangle MPN, l'angle PMN mesure 60.
Ces trois triangles sont donc semblables.
4. Joanna aimerait que le coefficient d’agrandissement pour passer du triangle PDN au triangle AMD soit plus petit que 1,5. Est-ce le cas ? Justifier.
Dans le triangle rectangle ADM : DM² = AM² +AD² =3,46² +2² = 15,97 ; DM ~ 4,0 m.
DM / DN = DM / AM = 4,0 / 3,46 ~1,16. C'est bien le cas.

Exercice 3 (17 points).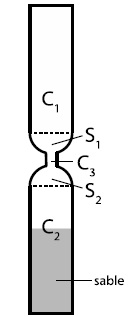

Les questions 1 et 2 sont indépendantes.
Un sablier est composé de
- Deux cylindres C₁ et C₂ de hauteur 4,2 cm et de diamètre 1,5 cm
- Un cylindre C₃
- Deux demi-sphères S₁ et S₂ de diamètre 1,5 cm
1.a. Au départ, le sable remplit le cylindre C₂ aux deux tiers. Montrer que le volume du sable est environ 4,95 cm³.
2 / 3 x3,14 x0,75² x4,2 ~4,95 cm³.
b. On retourne le sablier. En supposant que le débit d’écoulement du sable est constant et égal à 1,98 cm³/min, calculer le temps en minutes et secondes que va mettre le sable à s’écouler dans le cylindre inférieur.
4,95 / 1,98 ~2,5 min = 2 min 30 s.
2. En réalité, le débit d’écoulement d’un même sablier n’est pas constant.
Dans une usine où on fabrique des sabliers comme celui-ci, on prend un sablier au hasard et on teste plusieurs fois le temps d’écoulement dans ce sablier. Voici les différents temps récapitulés dans le tableau suivant :

temps mesuré	2 min 22 s	2 min 24 s	2 min 26 s	2 min 27 s	2 min 28 s	2 min 29 s	2 min 30 s	2 min 31 s	2 min 32 s	2 min 33s	2 min 34 s	2 min 35 s	2 min 38 s
nombre de tests	1	1	2	6	3	7	6	3	1	2	3	2	3

a. Combien de tests ont été réalisés au total ?
40 tests.
b. Un sablier est mis en vente s’il vérifie les trois conditions ci-dessous, sinon il est éliminé.
 L’étendue des temps est inférieure à 20 s
 La médiane des temps est comprise entre 2 min 29 s et 2 min 31 s
 La moyenne des temps est comprise entre 2 min 28 s et 2 min 32 s
Le sablier testé sera-t-il éliminé ?
Etendue = 158 -142 =16 s.
La médiane est comprise entre 2 min 29 et 2 min 30 s .
La moyenne des temps vaut : 2 min 30 s et un dixième.
Les trois conditions étant respectées, le sablier est mis en vente.

Exercice 4. ( 19 points).
On veut réaliser un dessin constitué de deux types d’éléments (tirets et carrés) mis bout à bout.
Chaque script ci-dessous trace un élément, et déplace le stylo.
On rappelle que « s’orienter à 90 » signifie qu’on oriente le stylo vers la droite.
1. En prenant 1 cm pour 2 pixels, représenter la figure obtenue si on exécute le script Carré.
Préciser les positions de départ et d’arrivée du stylo sur votre figure.

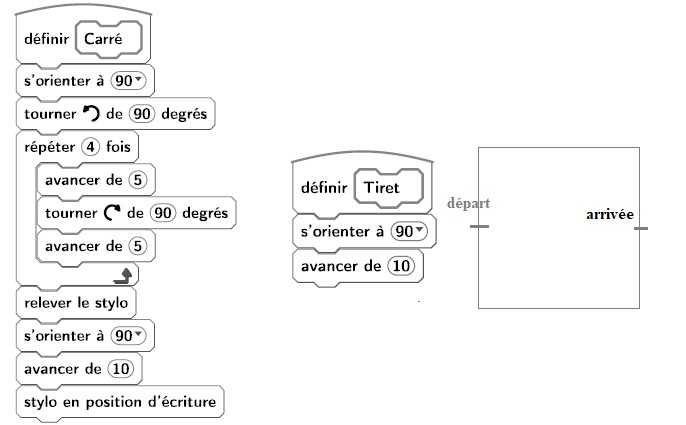
On obtient un carré de 10 pixels soit 5 cm de côté.
Pour tracer le dessin complet, on a réalisé 2 scripts qui se servent des blocs « Carré » et « Tiret » ci-dessus :

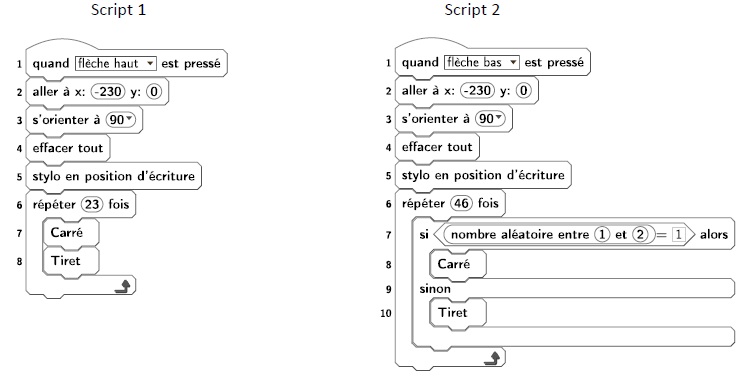
On exécute les deux scripts et on obtient les deux dessins ci-dessous.

2. Attribuer à chaque script la figure dessinée. Justifier votre choix.
Dessin B : script 1, alternance de carré et de tiret.
Dessin A : script 2 : suite aléatoire de carrés et de tirets.
3. On exécute le script 2.
a. Quelle est la probabilité que le premier élément tracé soit un carré ?
Deux valeurs sont possibles, la probabilité d'obtenir un carré vaut 0,5.
b. Quelle est la probabilité que les deux premiers éléments soient des carrés ?
4 possibilités : carré-carré ; carré - tiret ; tiret - carré ; tiret - tiret
La probabilité que les deux premiers éléments soient des carrés est 1 / 4 = 0,25.
4. Dans le script 2, on aimerait que la couleur des différents éléments, tirets ou carrés, soit aléatoire, avec à chaque fois 50 % de chance d’avoir un élément noir et 50 % de chance d’avoir un élément rouge.
Écrire la suite d’instructions qu’il faut alors créer et préciser où l’insérer dans le script 2.
Au niveau de la ligne 7 du script 2, on insére :
si nombre aléatoire entre 1 et 2 = 1 alors mettre la couleur du stylo à rouge sinon mettre la couleur du stylo à noir.

Exercice 5. ( 18 points).
Olivia s'est acheté un tableau pour décorer le mur de son salon.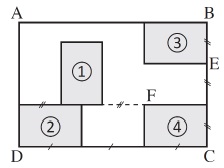

Ce tableau, représenté ci-contre, est constitué de quatre rectangles identiques dessinés à l’intérieur d’un grand
rectangle ABCD d’aire égale à 1,215 m². Le ratio longueur : largeur est égal à 3 : 2 pour chacun des cinq rectangles.
1. Recopier, en les complétant, les phrases suivantes. Aucune justification n’est demandée.
a. Le rectangle 3 est l'image du rectangle 4 par la translation qui transforme C en E.
b. Le rectangle 4 est l'image du rectangle 1 par la rotation de centre F et d'angle 90° dans le sens des aiguilles d'une montre.
c. Le rectangle ABCD est l'image du rectangle 2 par l'homothétie de centre D et de rapport 3.
(Il y a plusieurs réponses possibles, une seule est demandée.)
2. Quelle est l'aire d’un petit rectangle ?
Le grand rectangle est constitué de 9 petits rectangles.
1,215 / 9 = 0,135 m².
3. Quelles sont la longueur et la largeur du rectangle ABCD ?
La longueur est égale à 1,5 fois la largeur.
Largeur x1,5 largeur = 1,215 ; largeur² = 1,215 / 1,5 =0,81 ; largeur =0,9 m ; longueur = 0,9 x1,5 = 1,35 m.

Exercice 6. 17 points.
Voici deux programmes de calcul.

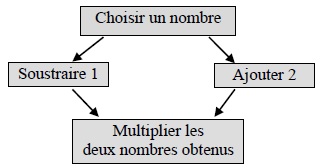
Programme 1	Programme 2
Choisir un nombre Le multiplier par 3 Ajouter 1

1. Vérifier que si on choisit 5 comme nombre de départ,
 Le résultat du programme 1 vaut 16.
 Le résultat du programme 2 vaut 28.
5 x3 +1 = 16 ; 5-1 = 4 ; 5+2 = 7 ; 4 x7 = 28.
On appelle A(x) le résultat du programme 1 en fonction du nombre x choisi au départ.
La fonction B = (x − 1)(x + 2) donne le résultat du programme 2 en fonction du nombre x choisi au départ.
2.a. Exprimer A(x) en fonction de x.
A(x) = 3x +1.
b. Déterminer le nombre que l’on doit choisir au départ pour obtenir 0 comme résultat du programme 1.
3x+1 = 0 ; 3x = -1 ; x = -1 /3.
3. Développer et réduire l'expression :
B(x) = (x − 1)(x + 2) = x² +2x-x-2 = x² +x-2.
4.a. Montrer que B(x) − A(x) = (x + 1)(x − 3).
B(x) − A(x) =x² +x-2-3x-1 = x²-2x-3.
(x + 1)(x − 3) = x²-3x+x-3 = x²-2x-3.
b. Quels nombres doit-on choisir au départ pour que le programme 1 et le programme 2 donnent
le même résultat ? Expliquer la démarche.
B(x) − A(x) =0 ; (x + 1)(x − 3)=0 ; x+1 = 0 soit x = -1 et x-3 = 0 soit x = 3.