Mathématiques, Brevet Centres étrangers 2019

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

Exercice 1 . ( 15 points )
Cet exercice est un questionnaire à choix multiples (QCM). Pour chaque question, une seule destrois réponses proposées est exacte. Sur la copie, indiquer le numéro de la question et recopier, sans justifier, la réponse choisie. Une bonne réponse rapporte 3 points ; aucun point ne sera enlevé en cas
de mauvaise réponse.
1. Quelle est la décomposition en produit de facteurs premiers de 28 ?
4 x7 ; 2 x14 ; 2²x7.
2. Un pantalon coûte 58 €. Quel est son prix en € après une réduction de 20% ? 38 ; 46,4 : 57,8.
58 x0,80 = 46,4 €.
3. Quelle est la longueur en m du côté [AC], arrondie au dixième près ? 6,5 ; 6,7 ; 24,1.

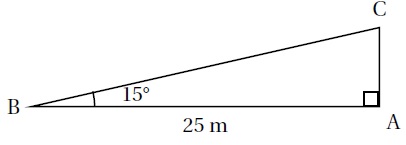
tan 15 = AC / AB = AC / 25 ; AC = 25 x tan 15 ~6,7 m.
4. Quelle est la médiane de la série statistique suivante ? 2; 5; 3; 12; 8; 6.
5,5 ; 6 ; 10.
On range les nombres par ordre croissant : 2 ; 3 ; 5 ; 6 ; 8 ; 12.
La médiane est comprise entre 5 et 6.
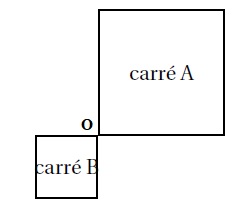
5. Quel est le rapport de l’homothétie qui transforme le carré A en carré B ? - 0,5 : 0,5 ; 2.

Exercice 2 ( 14 points).
On considère le programme de calcul :
• Choisir un nombre.
• Prendre le carré de ce nombre.
• Ajouter le triple du nombre de départ.
• Ajouter 2.
1. Montrer que si on choisit 1 comme nombre de départ, le programme donne 6 comme résultat.
1² =1 ; 1+3 = 4 ; 4+2 = 6.
2. Quel résultat obtient-on si on choisit −5 comme nombre de départ ?
(-5)² = 25 ; 25+3 (-5) = 10 ; 10+2 = 12.
3. On appelle x le nombre de départ, exprimer le résultat du programme en fonction de x.
x² +3x+2.
4. Montrer que ce résultat peut aussi s’écrire sous la forme (x+2)(x+1) pour toutes les valeurs de x.
On développe :(x+2)(x+1) =x²+x+2x+1 = x² +3x+2.
5. La feuille du tableur suivante regroupe des résultats du programme de calcul précédent.

	A	B	C	D	E	F	G	H	I	J
1	x	-4	-3	-2	-1	0	1	2	3	4
2	(x+2)(x+1)	6	2	0	0	2	6	12	20	30

a. Quelle formule a été écrite dans la cellule B2 avant de l’étendre jusqu’à la cellule J2 ?
=(B1+2)*(B1+1)
b. Trouver les valeurs de x pour lesquelles le programme donne 0 comme résultat.
x+2= 0 soit x = -2 ; x+1=0 soit x = -1.

Exercice 3 (16 points).
Partie I.
Dans cette partie, toutes les longueurs sont exprimées en centimètre.
On considère les deux figures ci-dessous, un triangle équilatéral et un rectangle, où x représente un nombre positif quelconque.

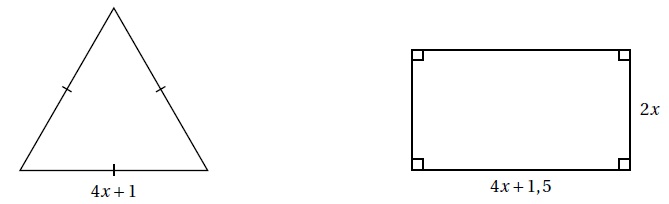
1. Construire le triangle équilatéral pour x = 2.
Mesure du côté du triangle équilatéral : 4 x 2 +1 = 9 cm.
2. a. Démontrer que le périmètre du rectangle en fonction de x peut s’écrire 12x +3.
2 (4x+1,5 +2x) = 2(6x+1,5 )= 12x +3.
b. Pour quelle valeur de x le périmètre du rectangle est-il égal à 18 cm ?
12x+3 = 18 ; 12x = 18-3 =15 ; x = 15 /12 = 5 /4 = 1,25.
3. Est-il vrai que les deux figures ont le même périmètre pour toutes les valeurs de x ? Justifier.
Périmètre du triangle : 3(4x+1) = 12 x+3 = périmètre du rectangle.
Partie II.
On a créé les scripts (ci-dessous) sur Scratch qui, après avoir demandé la valeur de x à l’utilisateur, construisent les deux figures de la
partie I. Dans ces deux scripts, les lettres A, B, C et D remplacent des nombres.
Donner des valeurs à A, B, C et D pour que ces deux scripts permettent de construire les figures de la partie 1 et préciser alors la figure associée à
chacun des scripts.

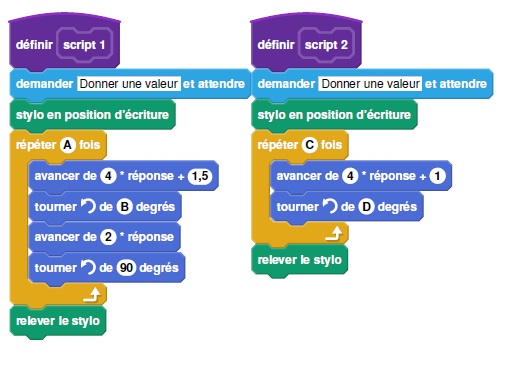
Le script 1 dessine le rectangle avec A = 2 et B = 90.
Le script 2 dessine le triangle avec C =3 et D = 120.

...

Exercice 4. ( 13 points).
Dans la vitrine d’un magasin A sont présentés au total 45 modèles de chaussures. Certaines sont conçues pour la ville, d’autres pour le sport et sont de trois couleurs différentes : noire, blanche ou marron.
1. Compléter le tableau suivant :

Modèle	Pour la ville	Pour le sport	Total
Noir	20-5 = 15	5	20
Blanc	7	18-5-3=10	7+10=17
Marron	27-7-15 =5	3	3+5=8
Total	27	45-27=18	45

2. On choisit un modèle de chaussures au hasard dans cette vitrine.
a. Quelle est la probabilité de choisir un modèle de couleur noire ?
20 / 45 = 4 / 9.
b. Quelle est la probabilité de choisir un modèle pour le sport ?
18 /45 = 2 /5
c. Quelle est la probabilité de choisir un modèle pour la ville de couleur marron ?
5 /45 = 1 /9.
3. Dans la vitrine d’un magasin B, on trouve 54 modèles de chaussures dont 30 de couleur noire.
On choisit au hasard un modèle de chaussures dans la vitrine du magasin A puis dans celle du magasin B.
Dans laquelle des deux vitrines a-t-on le plus de chance d’obtenir un modèle de couleur noire ? Justifier.
Dans A, la probabilité d'obtenir une chausure noire est 4 /9 ;
Dans B, la probabilité d'obtenir une chausure noire est 30 / 54 =5 /9. Réponse B.

Exercice 5. ( 10 points).
Un décorateur a dessiné une vue de côté d’un meuble de rangement composé d’une structure métallique et
de plateaux en bois d’épaisseur 2 cm. Les étages de la structure métallique de ce meuble de rangement sont tous identiques et la figure 2 représente
l’un d’entre eux.

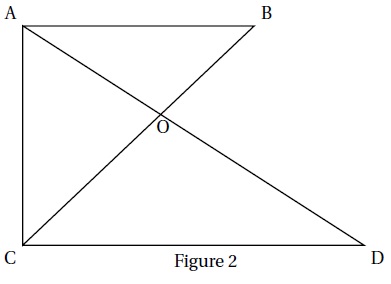
On donne :
• OC = 48 cm; OD = 64 cm; OB = 27 cm; OA = 36 cm et CD = 80 cm;
• les droites (AC) et (CD) sont perpendiculaires.
1. Démontrer que les droites (AB) et (CD) sont parallèles.
OA / OD = 36 / 64 =9 /16 ; OB / OC = 27 / 48 = 9 / 16.
OA / OD = OB / OC ; les droites (AB) et (CD) sont parallèles.
2. Montrer par le calcul que AB = 45 cm.
AB / CD= 9 / 16 ; AB = 9 x80 / 16 = 45 cm.
3. Calculer la hauteur totale du meuble de rangement.
4 étages + 5 épaisseur de bois = 4 AC +5 x 2 = 4 AC +10 cm.
Dans le triangle rectangle ABC : AC² = BC² -AB² =(27+48)² -45² =3600 ; AC = 60 cm.
Hauteur du meuble : 4 x60 +10 = 250 cm.

Exercice 6. 14 points.
Une famille a effectué une randonnée en montagne. Le graphique ci-dessous donne la distance parcourue en km en fonction du temps en heures.

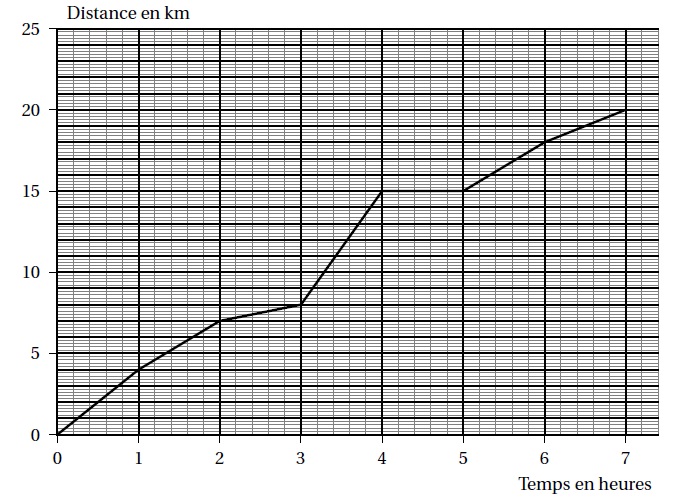
1. Ce graphique traduit-il une situation de proportionnalité? Justifier la réponse.
Non, le graphique n'est pas une droite passant par l'origine.
2. On utilisera le graphique pour répondre aux questions suivantes. Aucune justification n’est demandée.
a. Quelle est la durée totale de cette randonnée ? 7 heures.
b. Quelle distance cette famille a-t-elle parcourue au total ? 20 km.
c. Quelle est la distance parcourue au bout de 6 h demarche ? 18 km.
d. Au bout de combien de temps ont-ils parcouru les 8 premiers km ? 3 heures.
e. Que s’est-il passé entre la 4^e et la 5^e heure de randonnée ? Arrêt.
3. Un randonneur expérimenté marche à une vitesse moyenne de 4 km/h sur toute la randonnée. Cette famille est-elle expérimentée? Justifier la réponse.
6 heures de marche et 20 km parcourus ; vitesse moyenne : 20 / 6 = 10 /3 ~3,3 km / h.
La famille n'est pas expérimentée.

Exercice 7. 14 points.
Une famille désire acheter, pour les enfants, une piscine cylindrique hors sol équipée d’une pompe électrique. Elle compte l’utiliser cet été du mois de juin au mois de septembre inclus. Elle dispose d’un budget de 200 €.
À l’aide des documents suivants, dire si le budget de cette famille est suffisant pour l’achat de cette piscine et les frais de fonctionnement.

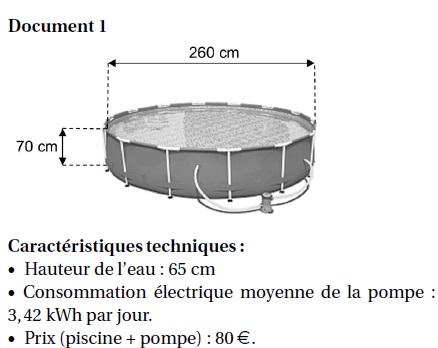
Prix d'un kWh : 0,15 € ; prix dun mètre cube d'eau : 2,03 €.
Volume d'eau : p r²h = 3,14 x1,3² x0,65 =3,45 m³. Coût : 3,45 x 2,03 = 7,00 €.
Consommation de la pompe durant 122 jours : 3,42 x122 = 417 kWh ; coût : 417 x0,15 = 62,59 €.
Total : 80 +62,59 +7,00 = 149,59 €.
Le budget est suffisant.