Mathématiques,
Nlle Calédonie 03/2019
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
.
.
|
|
Exercice
1 . ( 12 points )
Cet
exercice est un questionnaire à choix multiples (Q. C. M.). Pour chaque
question, une seule des trois réponses proposées est exacte. Sur la
copie, écrire le numéro de la question et la réponse choisie. On ne
demande pas de justifier. Aucun point ne sera enlevé en cas demauvaise
réponse.
|
Question
|
A
|
B
|
C
|
1
|
La décomposition en facteurs premiers de 1 600 est :
|
42 x102
4 et 10 ne sont pas premiers
|
28 x 52
256 x25 =6400
|
26 x 52
64 x25 =1600 Vrai
|
2
|
Sachant que (EF) // (MN) et EA = 2 cm; AM = 5 cm; EF = 4 cm
la longueur MN est égale à :
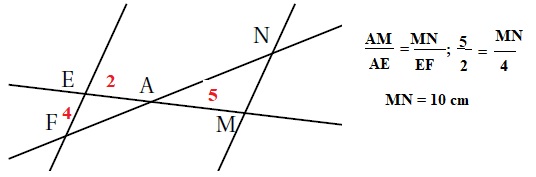
|
7 cm
|
10 cm
Vrai
|
1,6 cm
|
3
|
La forme développée et réduite de 6x(3x −5)+7x est : |
18x2 -23x. Vrai.
18x2 -30x +7x
|
-18x2 -30x + 7x
|
18x2 -37x.
|
| .
. |
Exercice
2 ( 9 points)
.Lors d’un voyage à Osaka, Jade a mangé des TAKOYAKI (gâteaux japonais) qu’elle veut refaire chez elle.
Pour cela, elle dispose d’une plaque de cuisson comportant plusieurs moules à gâteaux. Tous les moules sont identiques.
Chaque moule a la forme d’une demi-sphère de rayon 3 cm. Rappels : 1 L = 1 dm3.
Volume d’une boule de rayon r : V =4/3 p R3.
1. Calculer le volume d’un moule ¡en cm3, arrondir le résultat au dixième.
V = 4 / 3 x3,14 x33 =113,1 cm3.
Puis diviser par 2 : 56,5 cm3.
2. Dans cette question, on considère que le volume d’un moule est de 57 cm3..
Jade a préparé 1 L de pâte. Elle doit remplir chaque moule aux 3 /4 de son volume.
Combien de TAKOYAKI peut-elle faire ? Justifier la réponse.
Volume de pâte par moule : 57 x3 /4 = 42,75 cm3.
1 litre = 1000 cm3 ; 1000 / 42,75 ~23.
3. 12 points.
1. On considère la fonction g représentée dans le repère.
a. Donner l’antécédent de 4 par la fonction g .
L'antécédent de 4 est 2.
b. Compléter le tableau de valeurs de la fonction g .
x
|
-2
|
0
|
4
|
6
|
g(x)
|
12
|
8
|
0
|
-4
|
2. La fonction f est donnée par f (x) = 2x.
a. Quelle est l’image de −2 par la fonction f ?
f(-2) = 2 (-2) = -4.
b. Calculer f (3). f(3) = 2 *3 = 6.
c. Tracer la représentation graphique de la fonction f .
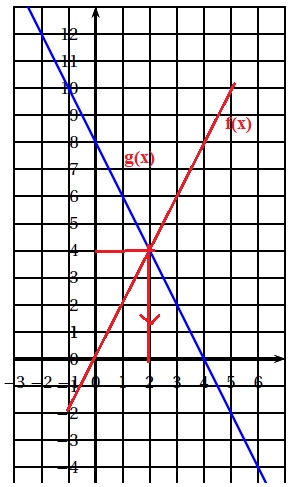
3. Déterminer graphiquement l’abscisse du point d’intersection S des deux représentations graphiques.
Faire apparaître en pointillés la lecture sur le graphique.
4. L’expression de la fonction g est g (x) = −2x +8.
a. Résoudre l’équation 2x = −2x +8
4 x = 8 soit x = 2.
b. Que représente graphiquement le résultat précédent ?
L'abscisse de l'intersection des deux droites.
|
|
......
...
|
|
|
|
|
Exercice 4. ( 12 points).
Calédorail est un projet de bus qui relierait différents points stratégiques de la ville de Nouméa.
1. Longueur de la ligne

La distance moyenne entre deux stations est d’environ 450 mètres. Estimer la distance entre la station 1 et la station 4.
3 x450 = 1350 m.
2. Vitesse moyenne
Le bus Calédorail mettrait 24 minutes pour effectuer un trajet de 9,9 km. Quelle serait sa vitesse moyenne en km/h ?
24 min = 24 / 60 = 0,4 heure.
Vitesse moyenne : 9,9 / 0,4 = 24,75 km / h.
3. Tarif
Actuellement, un ticket de bus coûte 190 F. Le ticket de bus Calédorail coûterait 40% plus cher.
Quel serait le prix du ticket de bus Calédorail ?
190 x1,4 = 266 F.
Exercice 5. ( 17 points).
Voici le classement des 21 pays ayant obtenu des médailles d’or lors des jeux olympiques d’hiver de Pyeongchang 2018 en Corée.

On considère la série constituée des nombres de médailles d’or obtenues par chaque pays.
Le classement est résumé dans la feuille de calcul ci-dessous :
|
A
|
B
|
C
|
D
|
E
|
F
|
G
|
H
|
I
|
J
|
K
|
L
|
1
|
Nombre de médailles
|
1
|
2
|
3
|
4
|
5
|
7
|
8
|
9
|
11
|
14
|
|
2
|
Effectif
|
6
|
3
|
1
|
1
|
4
|
1
|
1
|
1
|
1
|
2
|
21
|
1. a. Calculer le nombremoyen de médailles d’or par pays (arrondir le résultat au dixième).
Nombre total de médailles : 102 ; nombre de pays : 21 ; 102 / 21 = 4,86 ~4,9.
b. Déterminer la médiane des nombres de médailles d’or par pays.
c. Interpréter le résultat de la question 1. b.
21 /2 = 10,5 ; la médiane est la 11è valeur soit 4.
2. Quelle formule a-t-on saisie dans la cellule L2 pour obtenir le nombre total de pays ayant eu au moins une médaille d’or ?
= SOMME(B2 : K2)
3. On prend un pays au hasard parmi les pays qui ont au moins une médaille d’or.
a. Quelle est la probabilité qu’il ait une seule médaille d’or ? Donner la réponse sous forme fractionnaire.
6 / 21 = 2 / 7.
b. Quelle est la probabilité qu’il ait au moins 5 médailles d’or ? Donner la réponse sous forme fractionnaire.
Au moins 5 signifie 5, 7, 8, 9, 11, 14.
10 / 21.
Exercice6. 10 points.
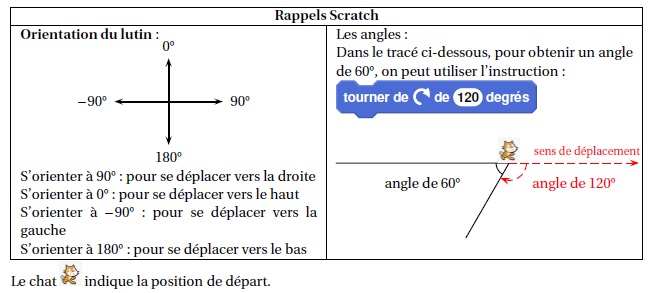
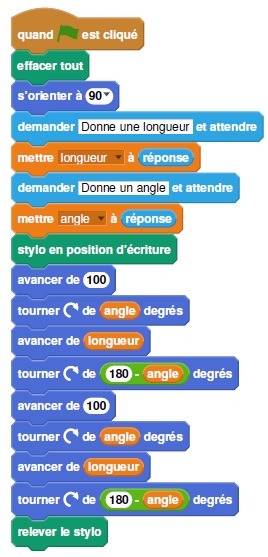
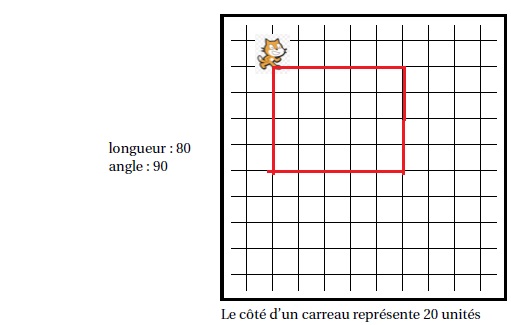
Voici ci-contre un programme réalisé avec Scratch pour construire un
parallélogramme. Selon la longueur et l’angle donnés, ce
parallélogramme peut être particulier (rectangle, losange, carré).
|
1. Dessiner le parallélogramme obtenu avec la longueur et l’angle donnés.
|
Quelle valeur faut-il donner à longueur et quelle valeur à angle pour obtenir la figure ci-dessous ?

Il faut mettre longueur à 100 et angle à 90°.
4. Un élève a choisi la longueur 50 et l’angle 75° puis a recopié la figure obtenue après exécution du script.
Lequel des trois parallélogrammes ci-dessous a-t-il tracé ?
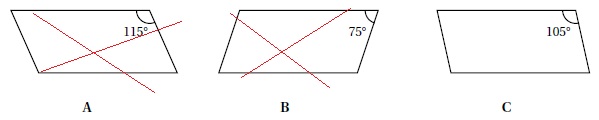
|
|
Exercice 7. 12 points.
Vrai ou faux en justifiant.
1. Le triangle ABC suivant est rectangle.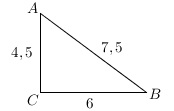 Vrai. Vrai.
7,5 2= 56,25.
4,52 + 62 = 56,25.
D'après la réciproque du théorème de Pythagore, ce triangle est rectangle.
2. Si un produit de 5 facteurs est strictement positif, alors aucun des facteurs n'est négatif. Faux.
Le produit de deux nombres négatifs ( ou de 4 nombres négatifs) est positif.
3. La maquette
ci-dessous représente une maquette du Phare Amédée qui a une hauteur de
56 m. Le rapport de réduction est égal à 1 /28.
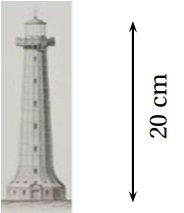 0,20 / 56 = 2 / 560 / 1 / 280. Affirmation fausse. 0,20 / 56 = 2 / 560 / 1 / 280. Affirmation fausse.
Exercice 8.
( 12 points )
Pour son confort, Lisa souhaite installer une voile d’ombrage triangulaire dans son jardin.
L’aire de celle-ci doit être de 8 m2 au minimum.
Pour chacun des trois modèles suivants indiquer sur la copie s’il convient en justifiant chaque réponse.
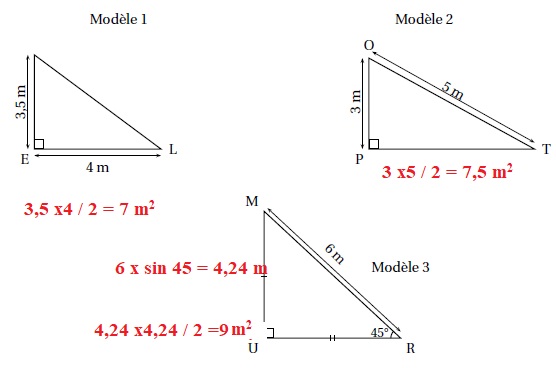
Le modèle 3 convient.
|
|