Newton
Car,
bac S Am�rique du nord 2019.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicit�s adapt�es � vos centres
d’int�r�ts.
.
.
|
|
Le � Newton Car � challenge, impuls�
par la NASA, est un d�fi scientifique qui peut �tre propos� aux �l�ves
de lyc�e.
Une � Newton Car � est compos�e d’un chariot de bois �quip� de trois
plots permettant de maintenir un �lastique �tir� � l’aide d’une
ficelle. Le chariot est positionn� sur une s�rie de pailles en
plastique.
Une masselotte est plac�e au niveau de la courbure de l’�lastique.
L’�jection de la masselotte met en mouvement le chariot.
L’objectif �tant de parcourir la
plus grande distance, c’est-�-dire d’avoir la plus grande vitesse au
d�marrage, les �l�ves sont amen�s � mesurer cette grandeur par
diff�rentes m�thodes.
� la date t = 0 s, le syst�me est immobile. On br�le la ficelle.
On observe alors le d�placement du chariot et de la masselotte dans la
m�me direction mais en sens oppos�.
Pour �tudier le mouvement de la � Newton Car �, on consid�re le syst�me
S constitu� de l’ensemble {chariot + ficelle + �lastique + masselotte}.
On note vC0 la vitesses du chariot et vmo
la vitesse de la masselotte juste apr�s la rupture de la ficelle.
Les mouvements sont �tudi�s dans le r�f�rentiel terrestre suppos�
galil�en.
Donn�es :
intensit� du champ de pesanteur : g = 9,81 m.s-2 ; masse
du chariot M = 200 g ; on note m la masse de la masselotte.
1.
Principe de propulsion de la � Newton Car �.
1.1. Apr�s avoir
br�l� la ficelle, faire l’inventaire des forces mod�lisant les actions
ext�rieures qui agissent sur le syst�me S.
Le syst�me est soumis � son poids ( verticale, vers le bas, valeur
(M+m)g ) et � l'action du support ( verticale, vers le haut ).
1.2. � quelle
condition le syst�me S peut-il �tre consid�r� comme pseudo-isol� ? Si
on suppose le syst�me pseudo-isol�, montrer que la quantit� de
mouvement du syst�me S est nulle.
Le syst�me est pseudo-isol� si les forces ext�rieures se compensent.
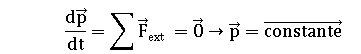
De plus la vitesse initiale est nulle ; en cons�quence la quantit� de
mouvement du syst�me est nulle.
1.3. D�terminer la
relation donnant la vitesse vC0 du chariot en fonction de la
vitesse vmo de la masselotte, de la masse M du chariot et de
la masse m de la masselotte. Pr�voir le sens du mouvement du chariot.
On n�glige les masses de la ficelle et de l’�lastique.
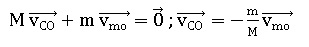
Chariot et masselotte se d�placent en sens contraire, le chariot allant
vers la gauche.
2. D�termination
de la vitesse du chariot par l’�tude d’un mouvement de chute
On installe la � Newton Car � au bord d’une table de hauteur h = 75,0
cm. Lorsque la ficelle est br�l�e, le chariot est propuls� avec une
vitesse initiale vC0 horizontale.
On �tudie le mouvement de la � Newton Car �, assimil�e � un point
mat�riel, dans le rep�re (xOz)donn� ci-dessous et on note P le point
d’impact au sol. L’exp�rience est r�p�t�e 10 fois afin d’augmenter la
qualit� de la mesure. On mesure � chaque fois au
sol l’abscisse xP du point de chute du chariot.
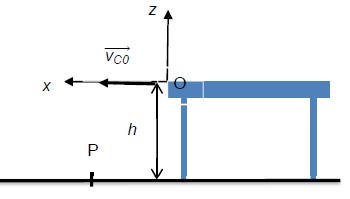
Les mesures sont consign�es dans le tableau ci-dessous :
xP
(cm)
|
65
|
66
|
61
|
62
|
61
|
63
|
59
|
65
|
60
|
63
|
2.1. Faire
l’inventaire des forces mod�lisant les actions qui s’exercent sur le
chariot lors de la chute (on n�glige l’action de l’air).
Le chariot �tant soumis uniquement � son poids, la chute est nibre.
2.2. Donner le
r�sultat de la mesure de xP accompagn� d’une �valuation de
son incertitude �largie pour un niveau de confiance de 95 %.
xP moyen = 62,5 cm ; �cart type : 2,3 : U(X) = 2 x 2,3 / 10�
~1,5.
xP =
63 � 2 cm.
2.3. Montrer que
les �quations horaires du mouvement du chariot s’�crivent :
x(t) = vC0.t et z(t)= - � g t2.
Composantes du vecteur acc�l�ration : ( 0 ; -g) .
Le vecteur vitesse est une primitive du vecteur acc�l�ration.
Vecteur vitesse initiale ( vCO ; 0) ; vecteur vitesse
: ( vCO ; -gt )
Le vecteur position est une primitive du vecteur vitesse : x(t)
= vC0.t et z(t)= - � g t2.
2.4. En d�duire la
valeur de la vitesse initiale vC0 en explicitant votre
d�marche.
Au sol : -h = - � g t2
; t =(2 h / g) � = (1,50 / 9,81)� =0,391 ;
xP =0,63 = vC0.t
; vCO = 0,63 / 0,391 = 1,6
m s-1.
|
|
|
3. D�termination de la vitesse du chariot
en utilisant l’effet Doppler.
On fixe un petit buzzer aliment� par une pile � l’avant du chariot
apr�s avoir rabot� une partie du chariot pour que la masse du syst�me
ne change pas.
On r�alise la m�me exp�rience que dans la partie 1.
3.1 �tude du son du
buzzer quand la � Newton Car � est immobile.
On enregistre le son �mis par le buzzer lorsque le dispositif est
immobile. L’enregistrement du signal sonore obtenu est repr�sent� sur
la figure 1 et son analyse spectrale sur la figure 2.
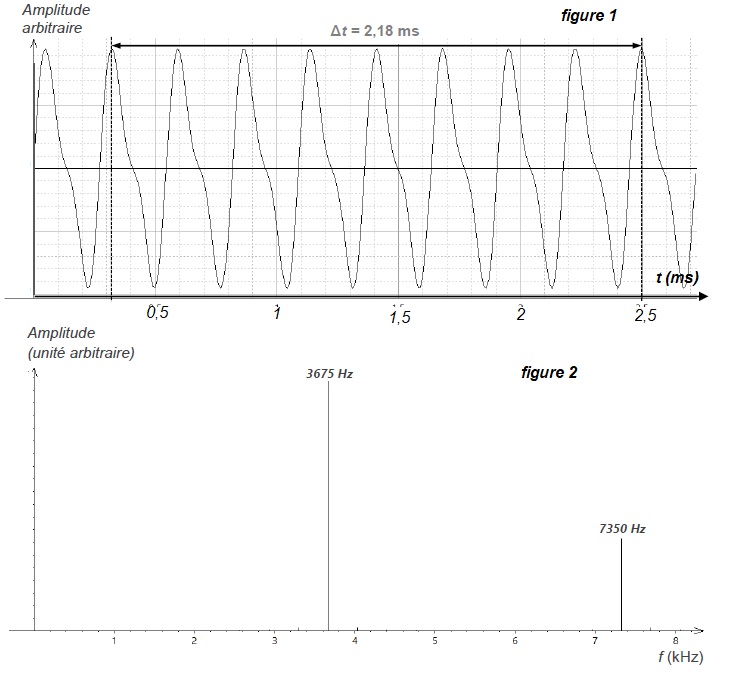
3.1.1. Comment
appelle-t-on chacun des pics qui appara�t sur le spectre du signal ?
Justifier.
Le premier pic est le fondamental et le second le pic de la premi�re
harmonique.
P�riode T = Dt /
8 = 2,18 10-3 / 8 = 2,725 10-4 s.
Fr�quence du fondamental : f= 1 /(2,725 10-4) =3,67 103
Hz.
Fr�quence de la premi�re harmonique : 2 x 3670 = 7,34 103 Hz.
3.1.2. Le son du
buzzer est-il pur ou complexe ? Justifier.
Le spectre du son est constitu� du fondamental et d'une harmonique. Le
son n'est donc pas pur mais complexe.
3.1.3. � partir de
l’enregistrement du signal (figure 1), d�terminer la fr�quence fE
du son �mis par le buzzer. Cette fr�quence est-elle en accord avec le
spectre du signal sonore �mis (figure 2) ?
Ecart relatif : (3,675 -3,67) / 3,675 x100 = 0,14 %.
L'�cart relatif �tant tr�s faible, il y a accord entre la fr�quence et
le spectre.
|
|
|
|
3.2 �tude du son du buzzer quand la
� Newton Car � est en mouvement.
On installe sur un support un microphone reli� � un ordinateur pour
permettre de faire l’acquisition du son du buzzer lorsque le chariot
passe devant le microphone. L’enregistrement est donn� sur la figure 3.
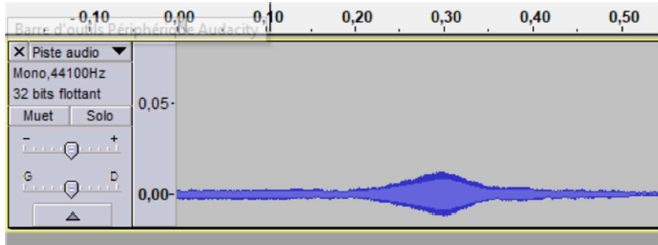
On s�lectionne une premi�re portion de signal correspondant �
l’approche du chariot. L’analyse spectrale indique une fr�quence f’R
= 3690 Hz.
On s�lectionne une deuxi�me portion de signal correspondant �
l’�loignement du chariot. L’analyse spectrale indique une fr�quence fR
= 3658 Hz.
3.2.1. Expliquer en
quelques lignes en quoi consiste l’effet Doppler.
On
appelle effet Doppler la modification de la fr�quence des ph�nom�nes
p�riodiques lorsque les syst�mes �changeant des signaux ont un
mouvement relatif.
Lorsqu'une ambulance munie d'une
sir�ne s'approche d'un observateur immobile, le son per�u est plus aigu
; il devient plus grave lorsque la sir�ne s'�loigne.
3.2.2. L’exp�rience
se d�roule � 25,0 �C. Quelle est alors la valeur de la propagation du
son dans l’air ?
v = 331 ( 1 +25 / 273) � =346 m /s.
3.2.3. Estimer la
valeur de la vitesse du chariot en explicitant votre d�marche.
Le r�cepteur s'approche de '�metteur : fR = fE (v
/ (v -vchariot)) ; fR / fE = v / (v -vchariot)
; v -vchariot =v fE / fR ;
vchariot =v(1- fE / fR )=346 (1-3675 /
3690) ~1,41 m /s.
Le r�cepteur s'�loigne de '�metteur : fR = fE (v
/ (v +vchariot)) ; fR / fE = v / (v +vchariot)
; v +vchariot =v fE / fR ;
vchariot =v(-1+ fE / fR )=346 (-1+3675
/ 3658) ~1,61 m /s.
Valeur moyenne : 1,51 m /s.
4. Optimisation de
la � Newton Car �
Lors de l’exp�rience conduite dans la partie 1, le chariot s’arr�te
lorsqu’il a parcouru une distance d = 246 cm. On suppose que la vitesse
initiale du chariot est �gale � 1,6 m.s-1. Pour simplifier
on mod�lise la situation en introduisant une force de frottement de
valeur constante.
4.1 Sachant que la
variation de l’�nergie m�canique d’un solide est �gale au travail des
forces non conservatives, d�terminer, dans le cadre de ce mod�le, la
valeur de la force de frottement.
Le poids et l'action normale du support, perpendiculaires � la vitesse,
ne travaillent pas.
La variation d'�nergie cin�tique est �gal au travail des frottements.
0-�mv2 = -f d ; f = 0,5 x0,200 x1,612 / 2,46
=0,1054 ~ 0,11 N.
4.2 Au vu de
l’ensemble de l’�tude r�alis�e, quels param�tres peut-on modifier pour
gagner le � Newton Car � challenge ?
Il faut augmenter la vitesse initiale du chariot : soit en diminuant sa
masse, soit en utilisant un �lastique plus raide et plus tendu ( on
augmente ainsi la vitesse initiale de la masselotte ).
|
|
|
